生成模型的两大代表：VAE和GAN

本文主要是介绍生成模型的两大代表：VAE和GAN，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

生成模型

给定数据集，希望生成模型产生与训练集同分布的新样本。对于训练数据服从\(p_{data}(x)\)；对于产生样本服从\(p_{model}(x)\)。希望学到一个模型\(p_{model}(x)\)与\(p_{data}(x)\)尽可能接近。

这也是无监督学习中的一个核心问题——密度估计问题。有两种典型的思路：

显式的密度估计：显式得定义并求解分布\(p_{model}(x)\)，如VAE。
隐式的密度估计：学习一个模型\(p_{model}(x)\)，而无需显式定义它，如GAN。

VAE

AE

首先介绍下自编码器（Auto Encoder, AE），它将输入的图像X通过编码器encoder编码为一个隐向量（bottleneck）Z，然后再通过解码器decoder解码为重构图像X’，它将自己编码压缩再还原故称自编码。结构如下图所示：

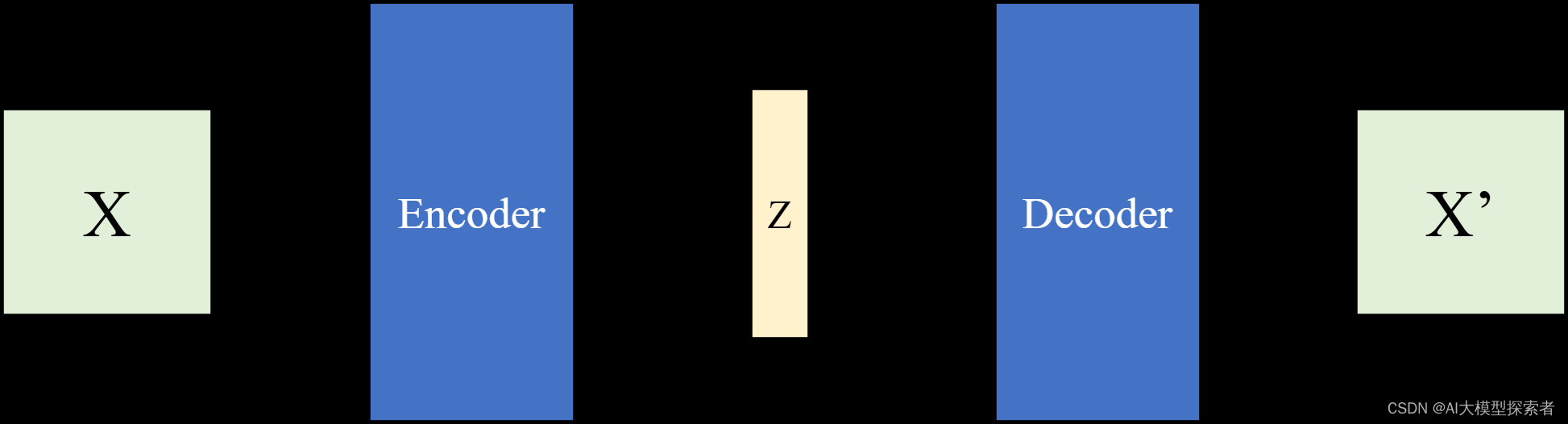
在这里插入图片描述

以手写数字数据集MNIST为例，输入图像大小为28x28，通道数为1，定义隐向量的维度（latent_dim）为1 x N，N=20。经过编码器编码为一个长度为20的向量，再通过解码器解码为28x28大小的图像。将生成图像X’与原始图像X进行对比，计算重构误差，通过最小化误差优化模型参数：

\[Loss = distance(X, X’) \]

一般distance距离函数选择均方误差（Mean Square Error, MSE）。AE与PCA作用相同，通过压缩数据实现降维，还能把降维后的数据进行重构生成图像，但PCA的通过计算特征值实现线性变换，而AE则是非线性。

VAE

如果中间的隐向量的每一分量取值不是直接来自Encoder，而是在一个分布上进行采样，那么就是变分自编码器（Variational Auto Encoder,VAE），结构如下图所示：

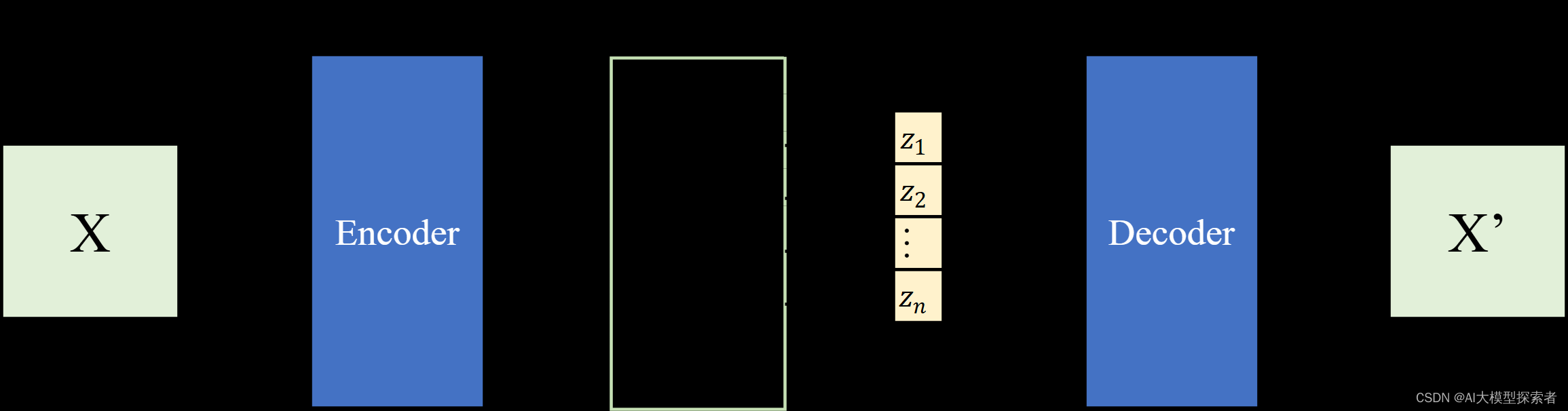
在这里插入图片描述

还是上面的例子，这里的Z维度还是1 x 20，但是每一分量不是直接来自Encoder，而是在一个分布上进行采样计算，一般来说分布选择正态分布（当然也可以是其他分布）。每个正态分布的\(\mu\)与\(\sigma\)由Encoder的神经网络计算而来。关于Z上每一分量的计算，这里，\(\epsilon\)从噪声分布中随机采样得到。

\[z^{(i,l)}=\mu{(i)}+\sigma^{{(i)}\cdot\epsilon}{(l)}\space\mathrm{and}\space\epsilon^{(l)}\sim N(0,I) \]

在Encoder的过程中给定x得到z就是计算后验概率\(q_\phi(z|x)\)，学习得到的z为先验分布\(p_\theta(z)\)，Decoder部分根据z计算x的过程就是似然估计\(p_\theta(x|z)\)，训练的目的也是最大化似然估计（给出了z尽可能得还原为x）。

边缘似然度\(p_\theta(x)=\int p_\theta(z)p_\theta(x|z)\,{\rm d}z\)，边缘似然度又是每个数据点的边缘似然之和组成：\(\log p_\theta(x^{{(1)},\cdots,x}{(N)})=\sum_{i=1}^N\log p_\theta(x^{(i)})\)，可以被重写为：

\[\log p_\theta(x^{(i)})={\rm D_{KL}}(q_\phi(z|x^{{(i)})||p_\theta(z|x}{(i)}))+{\cal L}(\theta,\phi;x^{(i)}) \]

\(p_\theta(z|x^{(i)})\)通常被假设为标准正态分布，等式右边第二项称为边缘似然估计的下界，可以写为：

\[\log p_\theta(x^{(i)})\ge{\cal L}(\theta,\phi;x^{(i)})=\mathbb{E}_{z\sim q_\phi(z|x)}[-\log q_\phi(z|x)+\log p_\theta(x|z)] \]

得到损失函数：

\[{\cal L}(\theta,\phi;x^{(i)})=-{\rm D_{KL}}(q_\phi(z|x^{(i)})||p_\theta(z))+\mathbb{E}_{z\sim q_\phi(z|x^{(i)})}[\log p_\theta(x^{(i)}|z)] \]

GAN

生成对抗网络（Generative Adversarial Nets, GAN）需要同时训练两个模型：生成器（Generator, G）和判别器（Discriminator, D）。生成器的目标是生成与训练集同分布的样本，而判别器的目标是区分生成器生成的样本和训练集中的样本，两者相互博弈最后达到平衡（纳什均衡），生成器能够以假乱真，判别器无法区分真假。

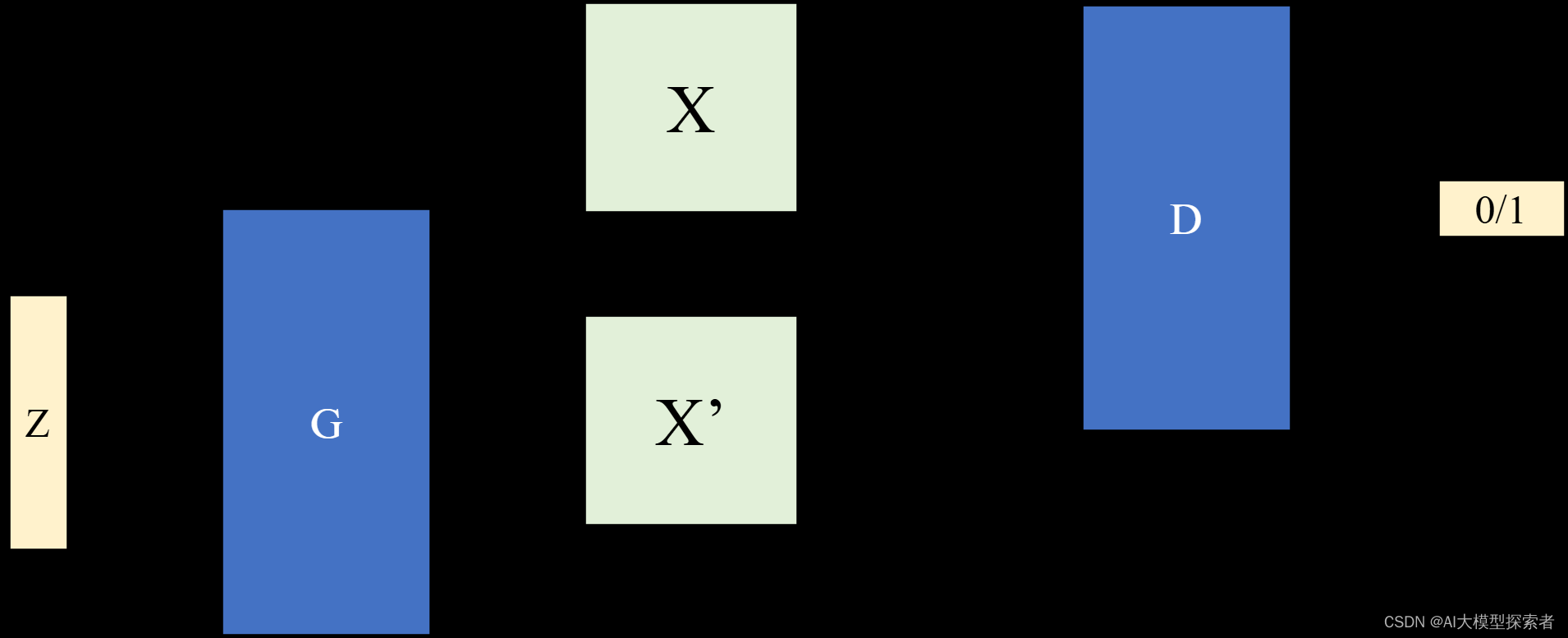
在这里插入图片描述

生成器和判别器最简单的应用就是分别设置为两个MLP。为了让生成器在数据x学习分布\(p_g\)，定义一个噪声分布\(p_z(z)\)，然后使用生成器\(G(z;\theta_g)\)将噪声映射为生成数据x’（\(\theta_g\)是生成器模型参数）。同样定义判别器\(D(x;\theta_d)\)，输出为标量表示概率，代表输入的x来自数据还是\(p_g\)。训练D时，以最大化分类训练样例还是G生成样本的概率准确性为目的；同时训练G以最小化\(\log(1-D(G(z)))\)为目的，两者互为博弈的双方，定义它们的最大最小博弈的价值函数\(V(G,D)\)：

\[\min_G\max_DV(D,G)=\mathbb{E}_{x\sim p_{data}}[\log D(x)]+\mathbb{E}_{z\sim p_{z}}[\log(1-D(G(z)))] \]

可以得到生成器损失函数：\(\mathcal{L}_G =\frac1m\sum_{i=1}^{m\log\left(1-D\left(G\left(z}{(i)}\right)\right)\right)\)

判别器损失函数：\(\mathcal{L}_D=\frac1m\sum_{i=1}^m\left[\log D\left(\boldsymbol{x}^{{(i)}\right)+\log\left(1-D\left(G\left(\boldsymbol{z}}{(i)}\right)\right)\right)\right]\)

极端情况下如果D很完美，\(D(x)=1,D(G(z))=0\)，最后两项结果都为0，但如果存在误分类，由于log两项结果会变为负数。随着G的输出越来越像x导致D误判，价值函数V也会随之变小。

计算它们的期望（\(\mathbb{E}_{x\sim p}f(x)=\int_xp(x)f(x){\rm d}x\)）：

\[V(G,D)=\int_xp_{data}(x)\log D(x)\,{\rm d}x+\int_zp_z(z)\log(1-D(G(z)))\,{\rm d}z \\ =\int_xp_{data}(x)\log D(x)+p_g(x)\log(1-D(x))\,{\rm d}x \]

当D取到最优解时，上面的最大最小博弈价值函数\(V(G,D)\)可以写为：

\[C(G)=\max_DV(G,D)= \\ \mathbb{E}_{x\sim p_{data}}[\log\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+\mathbb{E}_{x\sim p_g}[\log\frac{p_g(x)}{p_{data}(x)+p_g(x)}] \]

当\(p_g=p_{data}\)，取到\(-\log4\)，上式可以写成KL散度的形式：

\[C(G)=-\log4+{\rm KL}(p_{data}||\frac{p_{data}+p_g}{2})+{\rm KL}(p_g||\frac{p_{data}+p_g}{2}) \]

当\(p_g=p_{data}\)时，G取最小值也就是最优解。对于对称的KL散度，可以写成JS散度的形式：

\[C(G)=2\cdot{\rm JS}(p_{data}||p_g)-\log4 \]