本文主要是介绍java 霍夫曼解码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
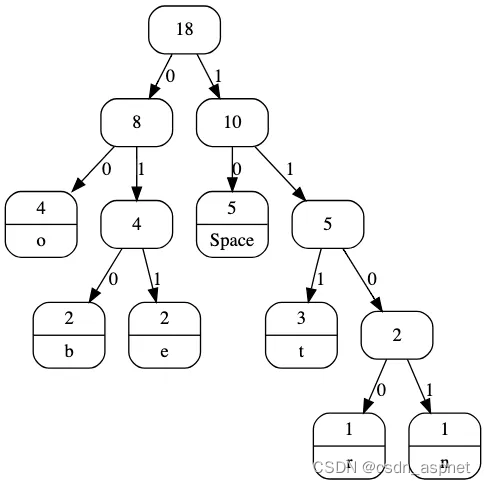
Huffman Tree 进行解码 示例图
c语言:c语言 霍夫曼编码 | 贪婪算法(Huffman Coding | Greedy Algo)_霍夫曼的贪婪c语言-CSDN博客
c++:c++ 霍夫曼编码 | 贪婪算法(Huffman Coding | Greedy Algo)_霍夫曼的贪婪算法设计核心代码-CSDN博客
c#:C# 霍夫曼编码 | 贪婪算法(Huffman Coding | Greedy Algo)-CSDN博客
c++ STL:c++ STL 霍夫曼编码 | 贪婪算法(Huffman Coding | Greedy Algo)-CSDN博客
java:java 霍夫曼编码 | 贪婪算法(Huffman Coding | Greedy Algo)-CSDN博客
python:python 霍夫曼编码 | 贪婪算法(Huffman Coding | Greedy Algo)-CSDN博客
javascript:JavaScript 霍夫曼编码 | 贪婪算法(Huffman Coding | Greedy Algo)-CSDN博客
我们在之前的文章中 讨论了霍夫曼编码。在这篇文章中,我们将讨论解码。
例子:
输入数据: AAAAAABCCCCCCDDEEEEE
频率: A:6,B:1,C:6,D:2,E:5
编码数据: 00000000000011001010101010111111110101010
哈夫曼树: “#”是用于内部节点的特殊字符,因为
内部节点不需要字符字段。
#(20)
/ \
#(12) #(8)
/ \ / \
A(6) C(6) E(5) #(3)
/ \
B(1) D(2)
‘A’ 的代码是 ‘00’,‘C’ 的代码是 ‘01’,..
解码数据: AAAAAAABCCCCCCDDEEEEE
输入数据: GeeksforGeeks
字符 频率为
e 10, f 1100, g 011, k 00, o 010, r 1101, s 111
编码的哈夫曼数据: 01110100011111000101101011101000111
解码的哈夫曼数据: geeksforgeeks
请按照以下步骤解决问题:
注意:要解码编码数据,我们需要霍夫曼树。我们遍历二进制编码数据。要找到与当前位对应的字符,我们使用以下简单步骤:
1、我们从根开始,依次进行,直到找到叶子。
2、如果当前位为 0,我们就移动到树的左节点。
3、如果该位为 1,我们移动到树的右节点。
4、如果在遍历过程中遇到叶节点,我们会打印该特定叶节点的字符,然后再次从步骤 1 开始继续迭代编码数据。
下面的代码将一个字符串作为输入,对其进行编码,并将其保存在变量编码字符串中。然后对其进行解码并打印原始字符串。
下面是上述方法的实现:
// Java program to encode and decode a string using
// Huffman Coding.
import java.util.*;
import java.util.Map.Entry;
public class HuffmanCoding {
private static Map<Character, String> codes = new HashMap<>();
private static Map<Character, Integer> freq = new HashMap<>();
private static PriorityQueue<MinHeapNode> minHeap = new PriorityQueue<>();
public static void main(String[] args) {
String str = "geeksforgeeks";
String encodedString = "";
String decodedString = "";
calcFreq(str);
HuffmanCodes(str.length());
System.out.println("Character With their Frequencies:");
for (Entry<Character, String> entry : codes.entrySet()) {
System.out.println(entry.getKey() + " " + entry.getValue());
}
for (char c : str.toCharArray()) {
encodedString += codes.get(c);
}
System.out.println("\nEncoded Huffman data:");
System.out.println(encodedString);
decodedString = decodeFile(minHeap.peek(), encodedString);
System.out.println("\nDecoded Huffman Data:");
System.out.println(decodedString);
}
private static void HuffmanCodes(int size) {
for (Entry<Character, Integer> entry : freq.entrySet()) {
minHeap.add(new MinHeapNode(entry.getKey(), entry.getValue()));
}
while (minHeap.size() != 1) {
MinHeapNode left = minHeap.poll();
MinHeapNode right = minHeap.poll();
MinHeapNode top = new MinHeapNode('$', left.freq + right.freq);
top.left = left;
top.right = right;
minHeap.add(top);
}
storeCodes(minHeap.peek(), "");
}
private static void calcFreq(String str) {
for (char c : str.toCharArray()) {
freq.put(c, freq.getOrDefault(c, 0) + 1);
}
}
private static void storeCodes(MinHeapNode root, String str) {
if (root == null) {
return;
}
if (root.data != '$') {
codes.put(root.data, str);
}
storeCodes(root.left, str + "0");
storeCodes(root.right, str + "1");
}
private static String decodeFile(MinHeapNode root, String s) {
String ans = "";
MinHeapNode curr = root;
int n = s.length();
for (int i = 0; i < n; i++) {
if (s.charAt(i) == '0') {
curr = curr.left;
} else {
curr = curr.right;
}
if (curr.left == null && curr.right == null) {
ans += curr.data;
curr = root;
}
}
return ans + '\0';
}
}
class MinHeapNode implements Comparable<MinHeapNode> {
char data;
int freq;
MinHeapNode left, right;
MinHeapNode(char data, int freq) {
this.data = data;
this.freq = freq;
}
public int compareTo(MinHeapNode other) {
return this.freq - other.freq;
}
}
//This code is contributed by NarasingaNikhil
输出:
具有以下频率的字符:
e 10
f 1100
g 011
k 00
o 010
r 1101
s 111
编码的哈夫曼数据:
01110100011111000101101011101000111
解码的哈夫曼数据:
geeksforgeeks
时间复杂度:
霍夫曼编码算法的时间复杂度为O(n log n),其中n为输入字符串的字符个数。辅助空间复杂度也是O(n),其中n为输入字符串的字符个数。
在给定的 Java 实现中,时间复杂度主要由使用优先级队列创建 Huffman 树决定,这需要 O(n log n) 时间。空间复杂度主要由用于存储字符频率和代码的映射决定,这需要 O(n) 空间。用于打印代码和存储代码的递归函数也增加了空间复杂度。
比较输入文件大小和输出文件大小:
比较输入文件大小和霍夫曼编码的输出文件。我们可以用一种简单的方法计算输出数据的大小。假设我们的输入是一个字符串“geeksforgeeks”,存储在文件 input.txt 中。
输入文件大小:
输入: “geeksforgeeks”
字符总数即输入长度:13
大小: 13 个字符出现次数 * 8 位 = 104 位或 13 个字节。
输出文件大小:
输入: “geeksforgeeks”
——————————————————
字符 | 频率 | 二进制哈夫曼值 |
——————————————————
e | 4 | 10 |
f | 1 | 1100 |
g | 2 | 011 |
k | 2 | 00 |
o | 1 | 010 |
r | 1 | 1101 |
s | 2 | 111 |
—————————————————
因此要计算输出大小:
e:出现 4 次 * 2 位 = 8 位
f:出现 1 次 * 4 位 = 4 位
g:出现 2 次 * 3 位 = 6 位
k:出现 2 次 * 2 位 = 4 位
o:出现 1 次 * 3 位 = 3 位
r:出现 1 次 * 4 位 = 4 位
s:出现 2 次 * 3 位 = 6 位
总和: 35 位,约 5 字节
由此可见,编码后的数据量是比较大的,上面的方法也可以帮我们确定N的值,也就是编码后数据的长度。
这篇关于java 霍夫曼解码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









