本文主要是介绍如何计算结构体变量的大小(结构体内存对齐),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、对齐规则
二、结构体大小计算三步曲
第一步:确定对齐数
第二步:根据对齐数确定每个成员相对位置
第三步:通过最大对齐数来确定结构体最终大小
三、内存浪费
四、为什么要存在内存对齐
在C语言中,变量由于类型不同在内存中开辟空间的大小不同,而结构体类型是一种特殊的变量类型,其可以是多个类型的集合,甚至结构体嵌结构体类型,那么结构体类型变量占内存空间的大小该如何计算呢?这也是一个特别热门的考点。
一、对齐规则
1.结构体的第一个成员对齐到和结构体变量起始位置偏移量为0的地址处。
2.其他成员变量要对齐到某个数字(对齐数)的整数倍的地址处。
对齐数 = 编译器默认的一个对齐数与该成员变量大小的较小值
VS 中默认的值为 8
Linux中gcc没有默认对齐数,对齐数就是成员自身的大小
3.结构体总大小为最大对齐数(结构体中每个成员变量都有⼀个对齐数,所有对齐数中最大的)的
整数倍。
4.如果嵌套了结构体的情况,嵌套的结构体成员对齐到自己的成员中最大对齐数的整数倍处,结构
体的整体大小就是所有最大对齐数(含嵌套结构体中成员的对齐数)的整数倍。
二、结构体大小计算三步曲
我们由此结构体举例说明(vs环境):
struct S3
{char c;double d;int i;
};
第一步:确定对齐数
找出每个成员变量的大小将其与编译器的默认对齐数相比较,取其较小值为该成员变量的对齐数。

第二步:根据对齐数确定每个成员相对位置
结构体变量地址为零下标,结构体的第一个成员对齐到和结构体变量起始位置偏移量为0的地址处,其他成员变量要对齐到对齐的整数倍的地址处。

第三步:通过最大对齐数来确定结构体最终大小
结构体总大小为最大对齐数(结构体中每个成员变量都有一个对齐数,所有对齐数中最大的)的
整数倍。
看上图:紫色部分(double d成员占用)+红色部分(char c成员占用)+绿色部分(int i成员占用)+红色与紫色之间的白色部分总共占用了20个字节的内存空间。而20并非最大对齐数8的整数倍,那么取8大于20的最小整数倍24为结构体最终大小。

三、内存浪费
由于对齐规则的存在,导致结构体虽然成员变量相同,但很可能会出现结构体大小不同的情况造成内存浪费。
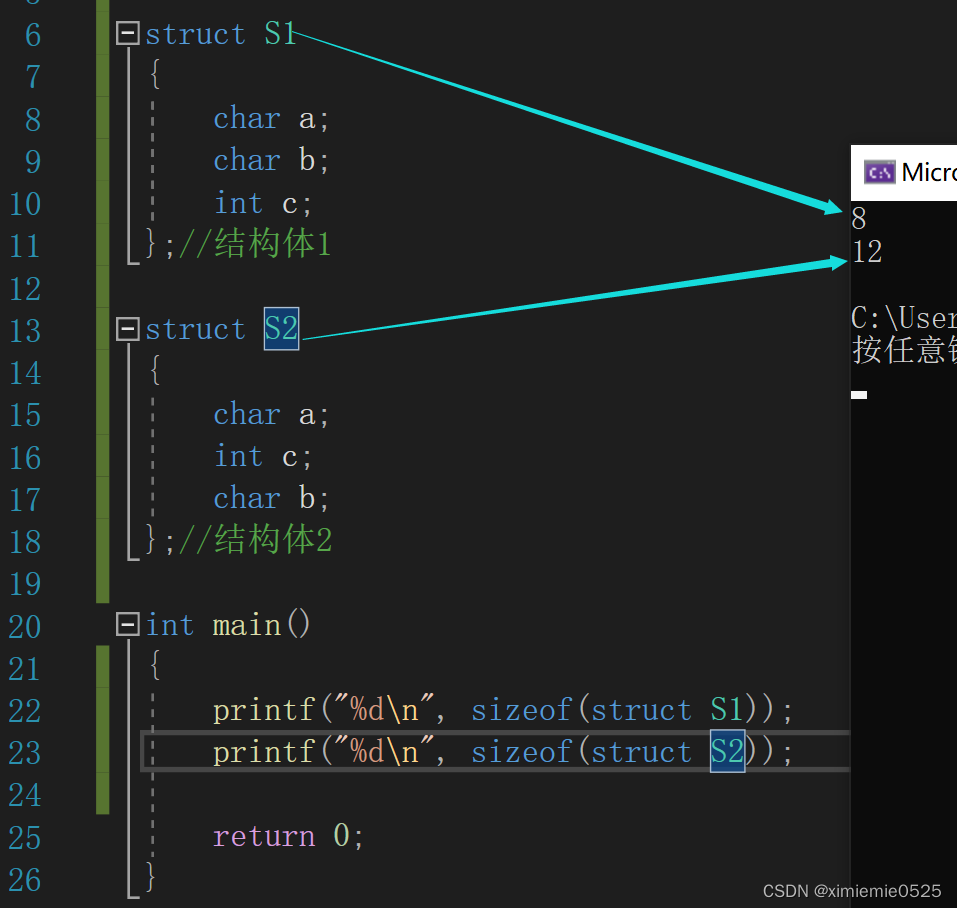
我们可以在构建结构体时,将每个成员变量的间隙在保证符合对齐规则的情况下尽量减小,这是一种合理且推荐使用的方法。
当然也可以使用#pragma pack( )的预处理来修改默认对齐数以达到减小空隙的效果,但是不推荐。详细见:C语言中#pragma pack(1)的用法_#pack(1)-CSDN博客
#include <stdio.h>#pragma pack(4)//设置默认对齐数为4
struct S1
{double a;//8/4->4int b;//4/4->4char c;//1/4->1
};//12
#pragma pack()//取消设置的默认对齐数,还原为默认#pragma pack(1)//设置默认对齐数为1
struct S2
{char a;//1/1->1int b;//4/1->1char c;//1/1->1
};//6
#pragma pack()//取消设置的默认对齐数,还原为默认int main()
{printf("%d\n", sizeof(struct S1));//打印结果为16printf("%d\n", sizeof(struct S2));//打印结果为6return 0;
}四、为什么要存在内存对齐
1. 平台原因(移植原因):
不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。
2. 性能原因:
数据结构(尤其是栈)应该尽可能地在自然然边界上对齐。原因在于,为了访问未对齐的内存,处理器需要作两次内存访问;而对齐的内存访问仅需要一次访问。假设一个处理器总是从内存中取8个字节,则地址必须是8的倍数。如果我们能保证将所有的double类型的数据的地址都对齐成8的倍数,那么就可以用一个内存操作来读或者写值了。否则,我们可能需要执行两次内存访问,因为对象可能被分放在两个8字节内存块中。
总体来说:结构体的内存对齐是拿空间来换取时间的做法。
这篇关于如何计算结构体变量的大小(结构体内存对齐)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





