本文主要是介绍递归与回溯 || 排列问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
前言:
全排列
题解:
全排列 II
题解:
子集
题解:
组合
题解:
组合总和
题解:
电话号码的字母组合
题解:
字母大小写全排列
题解:
优美的排列
题解:
前言:
递归与回溯问题需要弄清楚以下几点:
1、递归前需要做什么?
2、什么时候递归,什么时候回溯?
3、回溯时需要做什么,需要返回值吗,如何接收返回值,需要恢复现场吗,还是什么都不需要处理?
全排列
46. 全排列 - 力扣(LeetCode)

题解:
面对这种排列问题,首先需要画出决策树,根据决策树来实现代码!
我们以示例一为例,决策树如下:
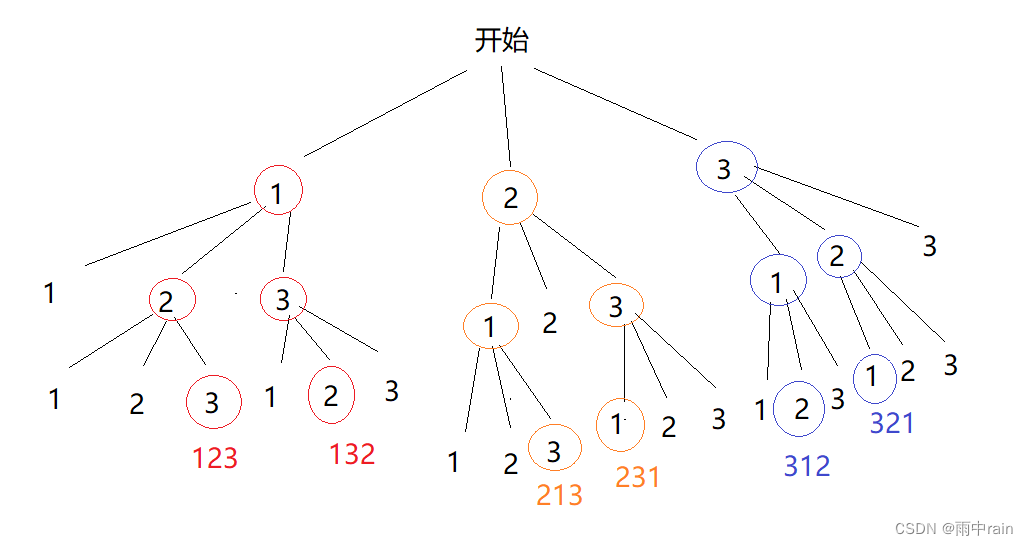
nums = [ 1, 2, 3 ], 假设我们选择排列的第一个数为 1,我们继续在 1 2 3 里面选择排列的第二个数,由于 1 已经被选过了,我们只能选择 2 或 3 作为排列的第二个数:
1、假设选择 2 为排列的第二个数,继续在 1 2 3 里面选择排列的第三个数,由于 1 2 已经被选过了,我们只能选择 3 作为排列的第三个数,最终排列的结果为 1 2 3 ;
2、假设选择 3 为排列的第二个数,继续在 1 2 3 里面选择排列的第三个数,由于 1 3 已经被选过了,我们只能选择 2 作为排列的第三个数,最终排列的结果为 1 3 2 。
选择 2 作为排列的第一个数也是同理。结合文字和图中的决策树可以看出,我们每次都会在 1 2 3 里面做选择,但每次选择时,会排除已经选过的数字(因为不能重复选)。
nums = [ 1, 2, 3, 4 ] 也是同样的道理(只截取一部分作为参考):

接下来我们需要回答开头提出的几个问题:
1、递归前需要做什么?
递归前需要找出排列的下一个数字。我们用 for 循环来模拟决策树做选择的过程,为了避免选择了重复的数字,我们用 bool 数组来标记,true 表示该数字已经选择过了,false 表示该数字还没有被选择过。如果找到了排列的下一个数字,把该数字添加到排列中,并把该数字标记为 true。
为了便于把数字尾插到排列中,我们把排列设计为全局变量。
2、什么时候递归?
找到排列的下一个数字后,就可以递归,寻找排列的下一个数。
3、什么时候回溯?
排列后的数组长度 == nums 的长度时,就可以回溯。
4、回溯时需要做什么?
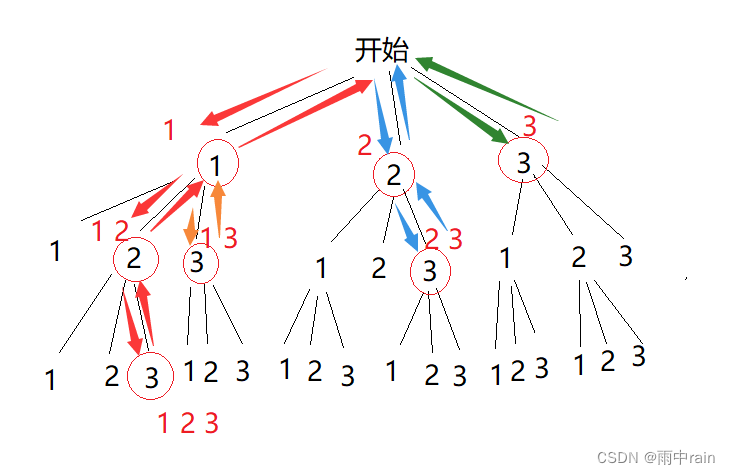
以 1 2 3 4 的排列为例,我们找到一个排列 1 2 3 4 之后(红色路径),需要从递归的最后一层回到 2 这一层,再选择 4 这个数字,继续递归(橙色路径),找出排列 1 2 4 3。这就要求我们:
1、从递归的最后一层 4 回溯到倒数第二层 3 时,把刚刚尾插到排列的数字 4 删掉,且把 4 置为 false(我们称这一操作为恢复现场),这样就可以把排列恢复到 1 2 3,然后继续回溯;
2、从递归的倒数第二层 3 回溯到 2 这一层时,当前排列为 1 2 3,我们把排列的最后一个数字删掉,并把 3 置为 false,这样就可以把排列恢复为 1 2,这样就可以接着递归橙色路径,找到排列 1 2 4 3。

总结:
回溯时需要 1、把当前排列的最后一个数字删掉; 2、把该数字置为 false 。
class Solution {vector<int> path;vector<vector<int>> ret;bool check[7];
public:vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size()==nums.size())//递归出口{ret.push_back(path);return;}for(int i=0;i<nums.size();i++)//模仿决策过程{if(check[i]==false)//该数字未访问过{path.push_back(nums[i]);check[i]=true;//把该数字设为访问过dfs(nums);//继续递归path.pop_back();//回溯时恢复现场check[i]=false;//把该数字恢复为未访问过}}}
};全排列 II
47. 全排列 II - 力扣(LeetCode)

题解:
这道题比较麻烦的是处理重复元素的排列,我们假设 nums = [ 1 ,1 ,1 ,2 ]:
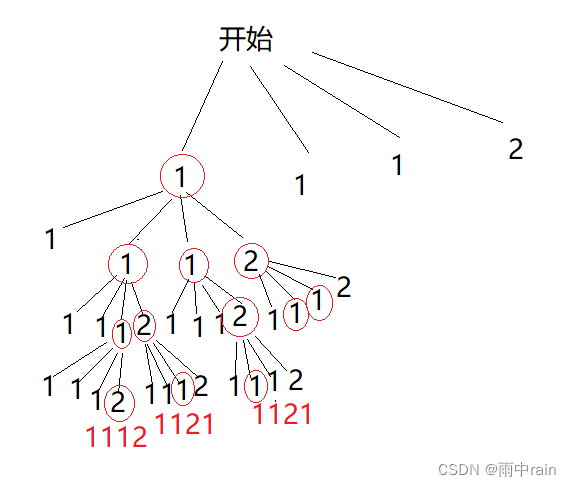
从部分决策树可以看出, 即使我们标记了哪个元素已经访问过了,依旧会出现重复的排列!所以我们需要观察得出排列的规律(先对 nums 进行排序,这样重复的数就会排在一起,便于讨论):
如果 nums[ i ] 还没有被访问过:
1、nums[ i ] 排在数组的第一个位置,那么 nums[ i ] 可以添加到排列;
2、 nums[ i ] 虽然不是数组的第一个元素,但是 nums[ i ] 和 nums[ i -1 ] 不相等,说明 nums[ i ] 可能在数组中只出现了一次,或者出现了很多次,但是 nums[ i ] 是这堆重复元素中第一个出现的,可以添加到排列中;
3、 nums[ i ] 不是数组的第一个元素,和 nums[ i -1 ] 相等了,但是 nums[ i -1 ] 已经被访问过了,那么可以添加到排列中。
因为递归是根据数组下标按从小到大的顺序添加到排列中的,若 nums [ i ] == nums[ i -1 ],对于同一层递归中,在访问 nums[ i ] 之前, nums[ i -1 ] 一定已经递归结束,且已经得出排列的结果了,而 nums[ i ] 和 nums[ i -1 ] 递归得到的排列是相同的,所以 nums[ i ] 没有必要进行递归了,所以剪枝!

class Solution {vector<vector<int>> ret;vector<int> path;bool check[9];
public:vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(),nums.end());dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos==nums.size())//回溯 {ret.push_back(path);return;}for(int i=0;i<nums.size();i++){//当前数字为false,或者这个数字是第一个数字,或者这个数字和前一个不相同,//或者这个数字和前一个相同,但是前一个数字为true,则可以继续递归if(check[i]==false && (i==0 || nums[i]!=nums[i-1] || check[i-1]==true)){path.push_back(nums[i]);check[i]=true;dfs(nums,pos+1);path.pop_back();//恢复现场check[i]=false;}}}
};子集
78. 子集 - 力扣(LeetCode)

题解:
决策树如下:
在挑选子集的时候,由于子集的无序性,子集 [ 1, 2 ] 和 [ 2, 1 ] 是相同的集合,为了避免结果中出现元素相同但顺序不同的集合,我们需要规定,在找子集时,不要回头去访问比子集的第一个元素小的数字。
比如决策树中,我们从 2 开始找子集,那我们就从 2 往后寻找元素,不要回头去访问比 2 小的数了,最终找到的子集就是 [ 2 ] , [ 2 , 3 ],从 3 开始找子集,就从 3 往后寻找元素,不要回头去访问比 3 小的数,最终找到的子集就是 [ 3 ] 。
为了实现这一规定,递归时需要记录上一层访问的数字,记为 pos,在 for 循环里面寻找元素时,从 pos 开始往后找。这其实是一个剪枝的操作!剪去了不必要的访问!
class Solution {vector<int> path;//子集vector<vector<int>> ret;
public:vector<vector<int>> subsets(vector<int>& nums) {ret.push_back(path);//空集dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos==nums.size()) return;for(int i=pos;i<nums.size();i++){path.push_back(nums[i]);ret.push_back(path);dfs(nums,i+1);path.pop_back();}}
};组合
77. 组合 - 力扣(LeetCode)

题解:
和子集类似,为了避免出现重复的组合,需要记录上一层访问的数字 start,用 for 循环寻找组合的元素时,只需要从 start 往后开始寻找,不要回头访问数字!
class Solution {vector<int> path;vector<vector<int>> ret;bool check[21];
public:vector<vector<int>> combine(int n, int k) {dfs(n,k,1);return ret;}void dfs(int n,int k,int start){if(path.size()==k){ret.push_back(path);return;}for(int i=start;i<n+1;i++){path.push_back(i);dfs(n,k,i+1);path.pop_back();}}
};组合总和
39. 组合总和 - 力扣(LeetCode)

题解:
决策树如下:

这道题规定一个数可以被无限重复次使用,所以我们不需要标记元素是否被访问过。
但是会出现重复的组合,比如 [ 2 , 2 , 3 ] 和 [ 3 , 2 , 2 ] 的组合总和都是 target,但是组合的元素相同,只是顺序不同,这样的组合就是重复的。为了避免出现重复的组合,我们要记录上一层访问的元素 pos,用 for 循环选择组合元素时,从 pos 往后开始选择,避免挑选组合的元素时走回头路。
这道题还需要注意递归的出口:
1、当 组合总和 == target 时,这个组合就是我们想要的组合,把该组合添加到结果数组,return;
2、如果 组合总和 > target ,已经没有继续寻找组合元素的必要了,return;
3、如果 组合总和 < target ,但是 组合总和+ candidates[ 0 ] > target (candidates 已排序),即 目前的组合总和 加上 candidates 最小的数 就已经超过 target,那么 目前的组合总和 无论加上 candidates 的哪个数,最终结果一定会大于 target,此时已经没有继续寻找的必要了,return。
class Solution {vector<vector<int>> ret;vector<int> path;int pathsum=0;
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());if(candidates[0]>target) return ret;dfs(candidates,target,0);return ret;}void dfs(vector<int>& candidates,int target,int pos){if(pathsum==target)//进结果{sort(path.begin(),path.end());ret.push_back(path); return;}//递归出口,后面再怎么加也不能凑出targetif(pathsum>target || pathsum+candidates[0]>target) return;for(int i=pos;i<candidates.size();i++){path.push_back(candidates[i]); pathsum+=candidates[i];dfs(candidates,target,i);//i决定了不会走回头路path.pop_back(); pathsum-=candidates[i];//恢复现场}}
};电话号码的字母组合
17. 电话号码的字母组合 - 力扣(LeetCode)

题解:
class Solution {vector<string> tel{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};string path;vector<string> ret;
public:vector<string> letterCombinations(string digits) {if(digits.size()==0) return ret;dfs(digits,0);return ret;}void dfs(const string& digits,int pos){if(pos==digits.size()){ret.push_back(path);return;}for(auto ch:tel[digits[pos]-'0'])//访问数字对应的字母{path.push_back(ch);//pos+1,访问下一个数字dfs(digits,pos+1);path.pop_back();//恢复现场}}
};字母大小写全排列
784. 字母大小写全排列 - 力扣(LeetCode)

题解:
这道题的决策树稍微有点不一样,有点类似二叉树,左子树是不变,右子树是变。

由于只需要改变大小写字母,在走 变 的这条分支时,如果当前访问的字符串为字母时,才需要大小写转换。
class Solution {vector<string> ret;string path;
public:vector<string> letterCasePermutation(string s) {dfs(s,0);return ret;}void dfs(const string& s,int pos){if(pos==s.size()){ret.push_back(path);return;}//不改变path.push_back(s[pos]);dfs(s,pos+1);path.pop_back();//改变if(s[pos]<'0' || s[pos]>'9'){char ch=change(s[pos]);path.push_back(ch);dfs(s,pos+1);path.pop_back();}}char change(char ch){if(ch>='a' && ch<='z') ch-=32;else ch+=32;return ch;}
};优美的排列
526. 优美的排列 - 力扣(LeetCode)

题解:
class Solution {int ret=0;bool check[16];
public:int countArrangement(int n) {dfs(n,1);return ret;}void dfs(int n,int i)//i为下标,pos为perm[i]{if(i==n+1){++ret;return;}for(int pos=1;pos<=n;pos++){if(!check[pos] && (pos%i==0 || i%pos==0)){check[pos]=true;dfs(n,i+1);check[pos]=false;}}}
};未完待续,欢迎读者指出文章的错误!
这篇关于递归与回溯 || 排列问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







