青蛙跳台阶问题的算法以及优化问题

本文主要是介绍青蛙跳台阶问题的算法以及优化问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法？
在遇到这种题目若是没有具体的思路之前，我们可以先列出前面几项的结果sum：
当 n = 1 时，青蛙仅有直接跳上一级台阶这种跳法，故 sum = 1;
当 n = 2 时，青蛙可以先跳上 1 级，然后再跳上 1 级到达2级台阶，共有2种跳法；若青蛙直接跳 2 级台阶，那么有1种跳法，从而 sum =2 + 1 = 3;
同理以上分析知道：
当 n = 3 时， sum = 5;
当 n = 4 时，sum = 8；
当 n = 5 时, sum = 13;
…
通过观察，我们发现其规律：
当 n = 1 时，sum = 1;
当 n = 2 时，sum = 2;
从第3项起，当前项的结果sum总是等于前两项的和，即有：
f(n) = f(n -1) + f( n -2) ,n > 2;
当我们看到这个规律时，便很容易想到这是 斐波那契数列
数学函数表示如下：
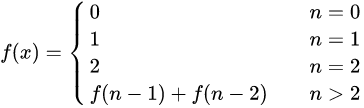
在这里插入图片描述
关于斐波那契数列的求解，我们有递归方法和非递归方法的求解，下面给出具体的递归算法：
在函数 int jumb(int n)中
（1）如果 n = 1 || n =2,直接返回结果 n;
（2）如果 n > 2，则计算返回 jumb(n -1) + jumb(n-2);
其具体代码实现为：

int jumb(int n) {if (n <= 0) {return 0;}//递归结束if (n == 1 || n == 2){return n;}//递归计算 f(n) = f( n -1 )+f( n - 2);return jumb(n -1) + jumb(n-2);
}

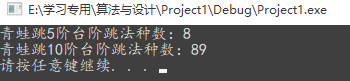
测试结果：

int main() {int n = 5;cout << "青蛙跳"<<n<<"阶台阶跳法种数：" << jumb(n) << endl;n = 10;cout << "青蛙跳" << n << "阶台阶跳法种数：" << jumb(n) << endl;system("pause");return 0;
}

在这里插入图片描述
下面笔者用图解来分析当 n =7 时该递归算法的调用情况：

该递归算法有两个问题，一个是变量能表示的最大数值有限制，另一个是递归深度有限制，递归深度太深，计算速度特别慢，在笔者的计算机上当 n = 50 时，笔者的电脑的散热扇狂转，CUP高速运转，等待了很久都没有得出答案。结合图示我们可以发现，在递归的过程中计算机要做很多重复的计算，比如图中计算 n = 7 时 ,f(4),f(3)，f(2),f(1)的值重复计算了很多次，这样就导致了计算机要花费更多的时间和空间资源进行计算，其算法的时间复杂度为 O（n^2）,空间复杂度为：O（n）。
下面我们可以对该递归算法进行改善：

int jumb(int n,int first ,int second) {if (n <= 0) {return 0;}//递归结束if (n == 1 || n == 2){return n;}if (n == 3){return first + second;}//递归计算 f(n) = f( n -1 )+f( n - 2);return jumb(n-1,second,second + first);
}

测试：

int main() {int n = 5;cout << "青蛙跳"<<n<<"阶台阶跳法种数：" << jumb(n,1,2) << endl;n = 40;cout << "青蛙跳" << n << "阶台阶跳法种数：" << jumb(n,1,2) << endl;system("pause");return 0;
}

在这里插入图片描述
可以看到其结果和之前的递归方法结果一致。当我们调用的时候，参数jumb(int n,int first ,int second) n表示跳的台阶数，first表示第1次的结果，second表示第2次的结果,分别为1和2.为了便于理解，请看图解：

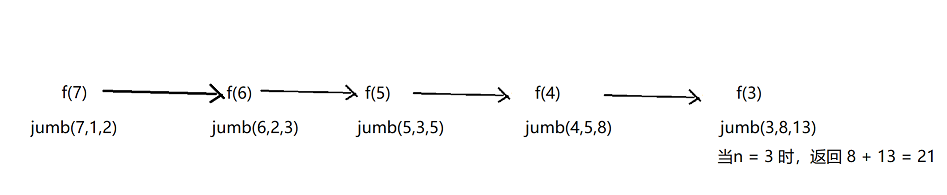
从图解我们可以发现，其实该递归函数实际上就是使用逆向迭代的方式计算结果：
当 n = 7 时， sum = 1 + 2;
当 n = 6 时， sum = 2 + 3;
当 n = 5 时， sum = 3 +5;
当 n = 4 时， sum = 5 + 8;
当 n = 3 时， sum = 8 + 13;退出循环，返回结果 sum = 21 ；
由于该递归算法是从尾部开始递归，所以该递归算法也称为：尾递归算法，根据图示我们可以发现尾递归算法只需要计算f(7)—>f(6)----> f(5) ----> f(4) ----->f(3),每个结果只计算一次，减少了那些没必要的重复计算，从而大大提高了程序的执行效率。其算法时间复杂度为：O（n），空间复杂度为：O（n）。
我们知道理论上说，任何一个递归的算法都可以转换为一个非递归算法，结合尾递归算法的实现，我们可以设计一个非递归的算法：

int Jumb(int n) {if (n <= 0) {return 0;}if (n == 1 || n == 2){return n;}//临时变量，也就是当 n= 1时的结果int a = 1;也就是当 n= 2时的结果//临时变量int b = 2;//记录总结果int sum = 0;for (int i = 3; i <= n;i++) {//计算f(n) = f( n -1 )+f( n - 2)sum = a + b;a = b;b = sum;}return sum;
}