本文主要是介绍智能优化算法:卷尾猴搜索算法-附代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
智能优化算法:卷尾猴搜索算法
文章目录
- 智能优化算法:卷尾猴搜索算法
- 1.算法原理
- 1.1 初始化种群
- 1.2 树上跳跃
- 1.3 卷尾猴的生命周期
- 1.4 地上跳跃
- 1.5 随机迁移
- 1.6 摇摆运动
- 1.7 攀爬运动
- 1.8 跟随者位置更新
- 2.实验结果
- 3.参考文献
- 4.Matlab
摘要:卷尾猴搜索算法( capuchin search algorithm,CapSA)是于2021年提出的一种新型智能优化算法,该算法模拟猴子的动态行为。通过对卷尾猴在森林中游荡觅食时的行为进行建模,设计了算法的基本优化特性。具有寻优能力强,收敛速度快等特点。
1.算法原理
卷尾猴种群包括两种类型:
(1)该群体的领导者,称为 α \alpha α领导者;
(2)追随者。其他卷尾猴也可能伴随领导者觅食,并追求类似的运动行为。
1.1 初始化种群
卷尾猴搜索算法与其他优化算法类似,在搜索范围内随机初始化种群:
x i = u b j + r × ( u b j − l b j ) (1) x^{i}=u b_{j}+r \times\left(u b_{j}-l b_{j}\right)\tag{1} xi=ubj+r×(ubj−lbj)(1)
其中 x i x^i xi为第 i i i个个体的位置, u b j ub_j ubj为个体的j维的上边界, l b j lb_j lbj为个体的 j j j维下边界, r r r为[0,1]之间的随机数。
1.2 树上跳跃
α \alpha α卷尾猴可以从一棵树跳到另一棵树,或者从一个树枝跳到同一棵树的另一个树枝。在这种情况下, α \alpha α卷尾猴的位置可以如式(2)所示:
x j i = F j + P b f ( v j i ) 2 sin ( 2 θ ) g , i < n / 2 ; 0.1 < ϵ ≤ 0.20 (2) x_{j}^{i}=F_{j}+\frac{P_{b f}\left(v_{j}^{i}\right)^{2} \sin (2 \theta)}{g}, i<n / 2 ; 0.1<\epsilon \leq 0.20 \tag{2} xji=Fj+gPbf(vji)2sin(2θ),i<n/2;0.1<ϵ≤0.20(2)
其中, x j i x_{j}^{i} xji 表示 α \alpha α 卷尾猴和其他卷尾猴在第 j j j 维的位置; F j F_{j} Fj 表示食物在第 j j j 维的位置; ϵ \epsilon ϵ 表示 [ 0 , 1 ] [0,1] [0,1] 内均匀生成的随机数; P b f P_{b f} Pbf 是卷尾猴在跳跃运动中提供平衡的概率; g g g 表示重力加速度,其值为 9.81 ; θ 9.81 ; \theta 9.81;θ 为卷尾猴的跳跃角度; τ \tau τ 是一个生命周期 Q \mathrm{Q} Q 参数,在整个迭代过程中系统性地 减少; v j i v_{j}^{i} vji 是第 i i i 只卷尾猴在第 j j j 维的速度。卷尾猴的跳跃角度 θ \theta θ 可如式 (3)所示:
θ = 3 2 r (3) \theta=\frac{3}{2} r \tag{3} θ=23r(3)
其中 r r r是在区间[0,1]内的随机数。
1.3 卷尾猴的生命周期
卷尾猴寿命指数函数 τ \tau τ,以在全局和局部搜索过程中实现探索和开采之间的平衡:
τ = β 0 e − β 1 ( k k ) β 2 (4) \tau=\beta_{0} e^{-\beta_{1}\left(\frac{k}{k}\right)^{\beta 2}}\tag{4} τ=β0e−β1(kk)β2(4)
其中, k k k 和 K K K 分别表示当前和最大迭代次数;参数 β 0 、 β 1 \beta_{0} 、 \beta_{1} β0、β1 和 β 2 \beta_{2} β2 值分别为 2 、 21 和 2 。 τ \tau τ 有利于CapSA有效地更新卷尾猴的位置,通过探索和开发周围区域快速定位食物位置,极大地影响了CapSA的准确性。 第 i i i 只卷尾猴的第 j j j 维的速度可计算如下:
v j i = ρ v j i + τ a 1 ( x b e s t j i − x j i ) + τ a 2 ( F j − x j i ) (5) v_{j}^{i}=\rho v_{j}^{i}+\tau a_{1}\left(x_{b e s t j}^{i}-x_{j}^{i}\right)+\tau a_{2}\left(F_{j}-x_{j}^{i}\right) \tag{5} vji=ρvji+τa1(xbestji−xji)+τa2(Fj−xji)(5)
其中, i = 1 , 2 , ⋯ , n i=1,2, \cdots, n i=1,2,⋯,n 表示 n n n 只卷尾猴个体的索引; j = 1 , 2 , ⋯ , d j=1,2, \cdots, d j=1,2,⋯,d 表示问题的维度; v j i v_{j}^{i} vji 是第 i i i 个卷尾猴在第 j j j 维的速度; x j i x_{j}^{i} xji 是第 i i i 只卷 尾猴的第 j j j 维的当前位置; x best j i x_{\text {best } j}^{i} xbest ji 表示第 i i i 只卷尾猴在第 j j j 维中的最佳位置; F j F_{j} Fj 表示食物在第 j j j 维的位置; a 1 a_{1} a1 和 a 2 a_{2} a2 是两个正常数,控制 x best j i x_{\text {best } j}^{i} xbest ji 和 F j F_{j} Fj 对卷尾猴速度的影响,其值均为 1 ; r 1 1 ; r_{1} 1;r1 和 r 2 r_{2} r2 是在 [ 0 , 1 ] [0,1] [0,1] 内的两个随机数;惯性系数 ρ \rho ρ 控制先前速度对运动的影响,该值取为 0.7 0.7 0.7 。
1.4 地上跳跃
α \alpha α卷尾猴可能会从一个地方跳到另一个地方,从河流的一边跳到另一边,或者用正常的行走来寻找食物。卷尾猴利用这种行为进行远距离行走,尤其是在树上食物匮乏的时候。在这种情况下,领导者和跟随卷尾猴的新位置可以确定如下:
x j i = F j + P e f P b f ( v j i ) 2 sin ( 2 θ ) g , i < n / 2 ; 0.2 < ϵ ≤ 0.30 (6) x_{j}^{i}=F_{j}+\frac{P_{e f} P_{b f}\left(v_{j}^{i}\right)^{2} \sin (2 \theta)}{g}, i<n / 2 ; 0.2<\epsilon \leq 0.30 \tag{6} xji=Fj+gPefPbf(vji)2sin(2θ),i<n/2;0.2<ϵ≤0.30(6)
其中, P e f P_{e f} Pef 表示卷尾猴在地面上运动的弹性概率; θ \theta θ 如式(3)所示。平衡系数 P b f P_{b f} Pbf 和弹性系数 P e f P_{e f} Pef ,都提供了有效的开发和探索,因为这些参数提高了局部和全局搜索方法的效率。经过深入分析后得出: 它 们的值分别为0.7和9。
另一方面, α \alpha α卷尾猴在正常行走时的新位置可以计算如下:
x j i = x j i + v j i , i < n / 2 ; 0.3 < ϵ ≤ 0.50 (7) x_{j}^{i}=x_{j}^{i}+v_{j}^{i}, i<n / 2 ; 0.3<\epsilon \leq 0.50\tag{7} xji=xji+vji,i<n/2;0.3<ϵ≤0.50(7)
1.5 随机迁移
在某些情况下,卷尾猴可能会随机搜索几个新的方向,以找到更好的食物。卷尾猴利用这种行为可以有效地探索森林,获得新的食物来源。这种卷尾猴在觅食过程中的随机迁移可以用数学公式表示如下:
x j i = τ × [ l b j + ϵ × ( u b j − l b j ) ] , i < n / 2 ; ϵ ≤ P r (8) x_{j}^{i}=\tau \times\left[l b_{j}+\epsilon \times\left(u b_{j}-l b_{j}\right)\right], i<n / 2 ; \epsilon \leq Pr \tag{8} xji=τ×[lbj+ϵ×(ubj−lbj)],i<n/2;ϵ≤Pr(8)
其中, P r Pr Pr是固定值为 0.1的正常数,表示卷尾猴的随机搜索概率; u b j u b_{j} ubj 和 l b j l b_{j} lbj 表示第 j j j 维搜索空间的上下界。卷尾猴的随机搜索可以利用随机特性和卷尾猴群集行为增强卷尾猴的全局搜索能力。它还可以增强局部搜索能力,避免局部最优解。
1.6 摇摆运动
一些 α \alpha α卷尾猴和其他伴生卷尾猴可能会通过小距离游荡,在树枝和树枝的所有尖端使用局部搜索来搜索食物。它们用尾巴抓住树枝,用摇摆行为在树枝两侧寻找食物。在这种情况下,卷尾猴的位置计算如下:
x j i = F j + τ P b f × sin ( 2 θ ) , i < n / 2 ; 0.5 < ϵ ≤ 0.75 (9) x_{j}^{i}=F_{j}+\tau P_{b f} \times \sin (2 \theta), i<n / 2 ; 0.5<\epsilon \leq 0.75 \tag{9} xji=Fj+τPbf×sin(2θ),i<n/2;0.5<ϵ≤0.75(9)
1.7 攀爬运动
在觅食过程中,一些 α \alpha α卷尾猴和其他追随卷尾猴可能会爬上树木及其树枝,并多次下树,这一过程类似于局部搜索。在这种情况下,卷尾猴的位置可计算如下:
x j i = F j + τ P b f ( v j i − v j − 1 i ) , i < n / 2 ; 0.75 < ϵ ≤ 1.0 (10) x_{j}^{i}=F_{j}+\tau P_{b f}\left(v_{j}^{i}-v_{j-1}^{i}\right), i<n / 2 ; 0.75<\epsilon \leq 1.0 \tag{10} xji=Fj+τPbf(vji−vj−1i),i<n/2;0.75<ϵ≤1.0(10)
其中, v j i v_{j}^{i} vji 是第 i i i 只卷尾猴第 j j j 维的速度, v j − 1 i v_{j-1}^{i} vj−1i 是第 i i i 只卷尾猴第 j j j 维的先前速度。
1.8 跟随者位置更新
模拟追随者跟随领导者时的行为:
x j i = 1 2 ( x j i + x j i − 1 ) n / 2 ≤ i ≤ n (11) x_{j}^{i}=\frac{1}{2}\left(x_{j}^{i}+x_{j}^{i-1}\right) \quad n / 2 \leq i \leq n \tag{11} xji=21(xji+xji−1)n/2≤i≤n(11)
其中, x j i x_{j}^{i} xji 表示当前跟随者的第 j j j 维位置; x j i − 1 x_{j}^{i-1} xji−1 表示先前跟随者的第 j j j 维位置; x ′ i j x^{\prime i} j x′ij 表示当前 α \alpha α 领导者的第 j j j 维位置。
算法伪代码
1: ϵ ← \epsilon \leftarrow ϵ← A random number generated between 0 and 1
2: P ← P \leftarrow P← A constant number equals to 0.5
3: Initialize the positions of the n capuchins using Equation 1 .
4: Evaluate the fitness of each capuchin’s position
5: Initialize the velocity of the capuchins
6: Randomly select some capuchins (<n / 2) to represent the leader and accompanying capuchins, where the remaining capuchins (followers) follow the leaders.
7: while (termination condition is not satisfied) do
8: Update the parameter τ \tau τ using Equation 4
9: for k = 1 \mathrm{k}=1 k=1 to n ( n= total number of capuchins (leaders and followers) ) do
10: \quad if (k<n / 2)(n / 2= the leader and the accompanying capuchins) then
11: Update the velocity of the leaders using Equation 5
12: \quad if ( ϵ ≥ 0.1 \epsilon \geq 0.1 ϵ≥0.1) then
13: \quad \quad if ( ϵ ≤ P \epsilon \leq P ϵ≤P) then
14: \quad \quad \quad if ( ϵ ≤ 0.2 \epsilon \leq 0.2 ϵ≤0.2) then
15: \quad Update the position of the leaders that leap on the trees using Equation 2
16: else if ( 0.2 < ϵ ≤ 0.30 0.2<\epsilon \leq 0.30 0.2<ϵ≤0.30) then
17: Update the position of the leaders that leap over riverbanks using Equation 6
18: else
Update the position of the leaders that walk on the ground using Equation 7
20 : end if
21: else if( 0.5 < ϵ ≤ 0.75 0.5<\epsilon \leq 0.75 0.5<ϵ≤0.75)
22: update the positon of the leaders that swing on tree branches using Equation 9
23: else if( 0.75 < ϵ ≤ 1 0.75<\epsilon \leq 1 0.75<ϵ≤1)
24: update the position of the leaders that climb on trees using Equation 10
25: end if
26: else
27: update the position of the leaders that relocate randomly using Equation 8
28: end if
29 : else
30: update the position of the followers using Equation 11
31: end if
32: end for
33: Calculate the fitness value of each capuchin
34: end while
35: The location of capuchins is the final optimal solution
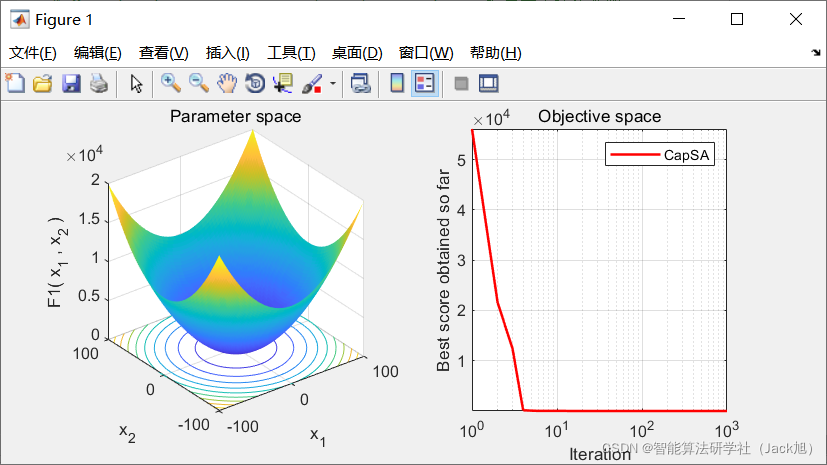
2.实验结果
3.参考文献
[1] Braik M , Sheta A , Al-Hiary H . A novel meta-heuristic search algorithm for solving optimization problems: capuchin search algorithm[J]. Neural Computing and Applications, 2021, 33(5).
4.Matlab
这篇关于智能优化算法:卷尾猴搜索算法-附代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







