智能优化算法：饥饿游戏搜索算法-附代码

本文主要是介绍智能优化算法：饥饿游戏搜索算法-附代码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

智能优化算法：饥饿游戏搜索算法

文章目录

智能优化算法：饥饿游戏搜索算法
- 1.算法原理
- - 1.1 接近食物
  - 1.2 饥饿角色
- 2.实验结果
- 3.参考文献
- 4.Matlab

摘要:饥饿游戏搜索算法(Hunger games search,HGS)是于2021年提出的一种新型智能优化算法，该算法是根据动物饥饿驱动活动和行为而设计的，具有寻优能力强，收敛速度快等特点。

1.算法原理

1.1 接近食物

动物接近食物的行为可以用式（1）表示：
$X(t+1)=\begin{cases} X(t)(1+randn(1)),r_1<l\\ W_1X_b+RW_2|X_b-X(t)|,r_1>l,r_2>E\\ W_1X_b-RW_2|X_b-X(t)|,r_1>l,r2<E \end{cases}\tag{1}$
其中， $R$ 是介于 $[- a, a]$ 的随机数； $r_1,r_2$ 均为[0,1]之间的随机数；randn是满足标准正态分布的随机数； $t$ 为当前迭代次数； $W_1$ 和 $W_2$ 表示饥饿权重； $X_b$ 表示全局最优位置； $X (t)$ 表示当前个体位置； $l$ 是设置的常数。 $E$ 的计算公式如下：
$E=sech(|F(i)-BF|)\tag{2}$
其中 $i\in(1,2,...,N)$ ， $F (i)$ 第 $i$ 个个体的适应度值； $B F$ 是当前最优适应度值。 $s e c h$ 是一个双曲函数。
$sech(x)=\frac{2}{e^x+e^{-x}} \tag{2}$
R的计算公式如下：
$\tag{4}$

$a=2*(1-t/Max_{iter})\tag{5}$

1.2 饥饿角色

对搜索中个体的饥饿特征进行了数学建模

$W_1$ 的计算如式（6）所示：
$W_1^i=\begin{cases} hungry(i)\frac{N}{SHungry}r_4,r3<l\\ 1,r3>l \end{cases}\tag{6}$
$W_2$ 的计算如式（7）所示：
$W_2^i=(1-exp(-|hungry(i)-SHungry|))*r_2*2 \tag{7}$
其中， $h u n g r y$ 表示每个个体的饥饿程度； $N$ 表示所有个体的总数； $S H u n g r y$ 表示所有个体饥饿程度的总和，即 $s u m (h u n g r y)$ ； $r_3,r_4,r_5$ 均为[0,1]之间的随机数。 $h u n g r y (i)$ 计算如下：
$hungry(i)=\begin{cases} 0,AllFitness(i)==BF\\ hungry(i)+H,else \end{cases}\tag{8}$
其中， $A l l F i t n e s s (i)$ 表示每个个体的适应度值。 $H$ 的计算如下：
$TH=\frac{F(i)-BF}{WF-BF}*r_6*2*(UB-LB)\tag{9}$

$H=\begin{cases} LH*(1+r),TH<LH\\ TH,else \end{cases}\tag{10}$

其中， $r_6$ 为[0,1]之间的随机数； $F (i)$ 为每个个体的适应度值； $B F$ 为当前最优适应度值； $W F$ 为当前最差适应度值； $U B$ 和 $L B$ 分别表示搜索空间的上限和下限； $L H$ 为 $H$ 的下界。

算法伪代码

Algorithm 1 Pseudo-code of Hunger Games Search (HGS)
Initialize the parameters N, T,l,D,SHungry
Initialize the positions of Individuals X i (i = 1,2,⋯,N)
While (t ≤ T)
Calculate the fitness of all Individuals
UpdateBF,WF,X b ,BI
Calculate the Hungry by Eq. (8)
Calculate the W 1  by Eq. (6)
Calculate the W 2  by Eq. (7)
For eachIndividuals
Calculate E by Eq. (2)
Update R by Eq. (4)
UpdatepositionsbyEq.(1)
End For
t = t + 1
End While
ReturnBF,X

2.实验结果

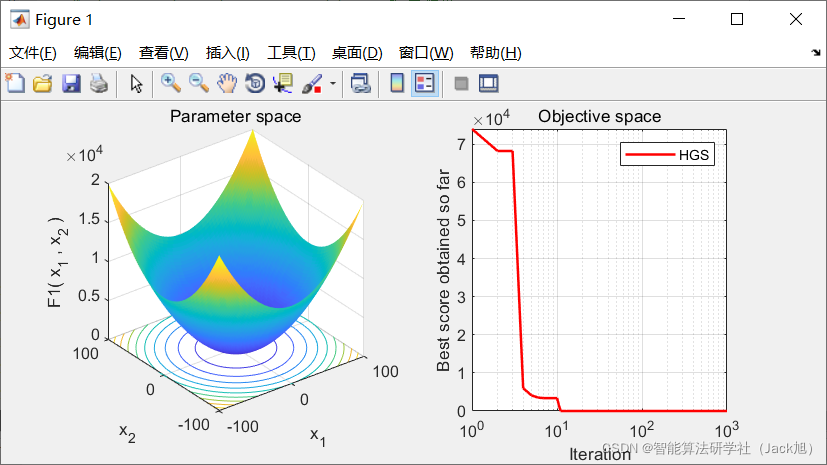
请添加图片描述

3.参考文献

[1] Yutao Yang, Huiling Chen, Ali Asghar Heidari, Amir H Gandomi. Hunger Games Search: Visions, Conception, Implementation, Deep Analysis, Perspectives, and Towards Performance Shifts[J]. Expert Systems with Applications, 2021, 177: 114864.