本文主要是介绍AcWing 1273:天才的记忆 ← ST算法求解RMQ问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【题目来源】
https://www.acwing.com/problem/content/1275/
【题目描述】
从前有个人名叫 WNB,他有着天才般的记忆力,他珍藏了许多许多的宝藏。
在他离世之后留给后人一个难题(专门考验记忆力的啊!),如果谁能轻松回答出这个问题,便可以继承他的宝藏。
题目是这样的:给你一大串数字(编号为 1 到 N,大小可不一定哦!),在你看过一遍之后,它便消失在你面前,随后问题就出现了,给你 M 个询问,每次询问就给你两个数字 A,B,要求你瞬间就说出属于 A 到 B 这段区间内的最大数。
一天,一位美丽的姐姐从天上飞过,看到这个问题,感到很有意思(主要是据说那个宝藏里面藏着一种美容水,喝了可以让这美丽的姐姐更加迷人),于是她就竭尽全力想解决这个问题。
但是,她每次都以失败告终,因为这数字的个数是在太多了!
于是她请天才的你帮他解决。如果你帮她解决了这个问题,可是会得到很多甜头的哦!
【输入格式】
第一行一个整数 N 表示数字的个数。
接下来一行为 N 个数,表示数字序列。
第三行读入一个 M,表示你看完那串数后需要被提问的次数。
接下来 M 行,每行都有两个整数 A,B。
【输出格式】
输出共 M 行,每行输出一个数,表示对一个问题的回答。
【数据范围】
1≤N≤2×10^5,
1≤M≤10^4,
1≤A≤B≤N。
【输入样例】
6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3
【输出样例】
34
123
123
8
【算法分析】
● ST算法(Sparse Table,稀疏表):https://blog.csdn.net/hnjzsyjyj/article/details/103429761
● 信息学竞赛中,经常会出现RMQ问题,即求区间最大(小)值问题。那么,我们该如何求解呢?ST算法横空出世。
ST算法(Sparse Table,稀疏表)主要用于解决区间最值问题(即RMQ问题)。因为ST算法求解RMQ问题时的时间复杂度只有O(nlogn),查询时间复杂度为常数阶O(1),所以我们还常称ST算法为TLE的死敌。虽然还可以使用线段树、树状数组、splay等算法求解区间最值问题,但是ST算法比它们更快,更适用于在线查询。
ST算法分成两部分:离线预处理O(nlogn)和在线查询O(1)。
(1)离线预处理:运用DP思想求解区间最值,并将结果保存到一个二维数组中。
(2)在线查询:对给定区间进行分割,并借助上步中的二维数组求最值
● 本题利用了ST算法求解RMQ问题,ST算法分预处理及询问两部分。要理解ST算法,首先要注意下文表述中的移位运算符 >>及<< 的优先级比四则运算 +-*/ 的优先级高。这样就能理解 1<<(j-1) 及 1<<j-1 代表不同的运算,即 1<<(j-1) 等价于 2^(j-1), 1<<j-1 等价于 2^j-1。
1. 预处理
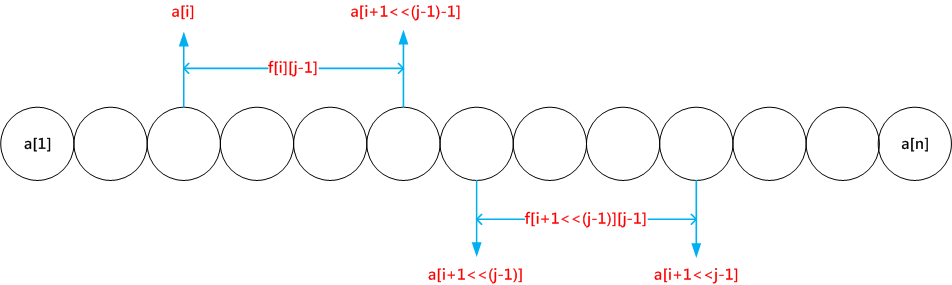
ST算法首先约定用 a[1] ~ a[n] 表示给定的一组数,f[i][j]表示从 a[i] ~ a[i+1<<j-1] 范围内的最大值,也即以 a[i] 为起点的连续 2^j 个数的最大值(∵ a[x] ~ a[y] 包含有 y-x+1 个数)。由于ST算法用到了倍增思想,因此自然有将 2^j 个数从中间平均分成两等分的实践,显然每一部分有 1<<(j-1) 个数,即2^(j-1) 个数。显然,初始范围 a[i] ~ a[i+1<<j-1] 被等分后,第一部分范围为 a[i] ~a[i+1<<(j-1)-1],第二部分范围为 a[i+1<<(j-1)] ~ a[i+1<<j-1],分别对应于f[i][j-1]和f[i+1<<(j-1)][j-1]。
综上,得 f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1])
2. 查询
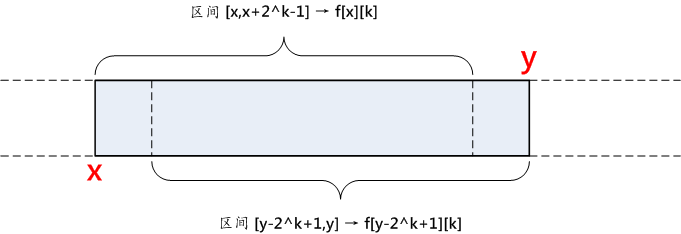
若给定查询区间 [x,y],若利用ST算法求此区间内的最大值。则需先求出最大的 k,使之满足 2^k ≤ y-x+1。
在此基础上,区间 [x,y]=[x,x+2^k-1]∪[y-2^k+1,y],则区间 [x,y] 内的最大值为 max(f[x][k],f[y-(1<<k)+1][k]) 。
据上,利用ST算法查询区间 [x,y] 的最大值,计算式如下:
k=log2(y-x+1)
max(f[x][k],f[y-(1<<k)+1][k])
【算法代码】
#include<bits/stdc++.h>
using namespace std;const int maxn=2e5+5;
const int maxm=18; //∵log(2e5)<18
int a[maxn];
int f[maxn][maxm]; //f[i][j]表示从i位起的2^j个数中的最大数int main() {int n,m,x,y;scanf("%d",&n);for(int i=1; i<=n; i++) {scanf("%d",&a[i]); //数组a的下标从1开始f[i][0]=a[i]; //f[i][0]表示[i,i]中的最大值,只能是a[i],故f[i][0]=a[i]}for(int j=1; j<=log2(n); j++)for(int i=1; i+(1<<j)-1<=n; i++) //注意i的右端点为i+(1<<j)-1,不能越界f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); //预处理scanf("%d",&m);for(int i=1; i<=m; i++) { //查询scanf("%d%d",&x,&y);int k=log2(y-x+1);printf("%d\n",max(f[x][k],f[y-(1<<k)+1][k]));}return 0;
}/*
in:
6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3out:
34
123
123
8
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/103429761
https://www.acwing.com/solution/content/14969/
这篇关于AcWing 1273:天才的记忆 ← ST算法求解RMQ问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






