Deep Forest，非神经网络的深度模型

欢迎转载，转载请注明：本文出自Bin的专栏blog.csdn.net/xbinworld。 

深度学习最大的贡献，个人认为就是表征学习（representation learning），通过端到端的训练，发现更好的features，而后面用于分类（或其他任务）的输出function，往往也只是普通的softmax（或者其他一些经典而又简单的方法）而已，所以，只要特征足够好，分类函数本身并不需要复杂——博主自己在做research的时候也深有同感，以前很多paper其实是误入歧途，采用的feature非常混淆模糊没有区分性，却指望在分类器上获得好的结果，可能么？深度学习可以说是回到了问题的本源上来，representation learning。

目前DL的成功都是建立在多层神经网络的基础上的，那么这种成功能否复刻到其他模型上呢？我相信，是可以的。南京大学的周志华老师尝试提出一种深度的tree模型，叫做gcForest，用文中的术语说，就是“multi-Grained Cascade forest”，多粒度级联森林。此外，还提出了一种全新的决策树集成方法，使用级联结构让 gcForest 做表征学习。

Title：Deep Forest: Towards An Alternative to Deep Neural Networks 
作者：Zhi-Hua Zhou and Ji Feng

摘要

在这篇论文里，我们提出了 gcForest，这是一种决策树集成方法（decision tree ensemble approach），性能较之深度神经网络有很强的竞争力。深度神经网络需要花大力气调参，相比之下 gcForest 要容易训练得多。实际上，在几乎完全一样的超参数设置下，gcForest 在处理不同领域（domain）的不同数据时，也能达到极佳的性能。gcForest 的训练过程效率高且可扩展。在我们的实验中，它在一台 PC 上的训练时间和在 GPU 设施上跑的深度神经网络差不多，有鉴于 gcForest 天然适用于并行的部署，其效率高的优势就更为明显。此外，深度神经网络需要大规模的训练数据，而 gcForest 在仅有小规模训练数据的情况下也照常运转。不仅如此，作为一种基于树的方法，gcForest 在理论分析方面也应当比深度神经网络更加容易。[1]

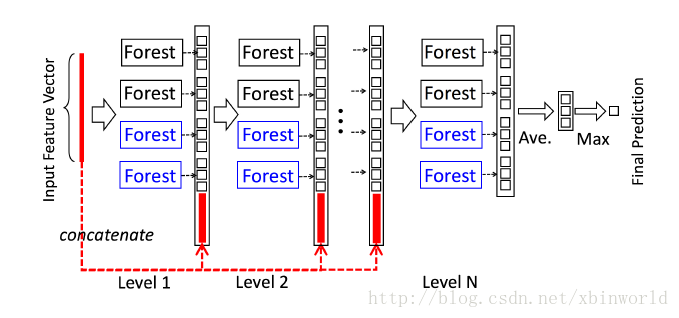
级联森林（Cascade Forest）

级联森林结构的图示。级联的每个级别包括两个随机森林（蓝色字体标出）和两个完全随机树木森林（黑色）。假设有三个类要预测; 因此，每个森林将输出三维类向量，然后将其连接以重新表示原始输入。注意，要将前一级的特征和这一级的特征连接在一起——在最后会有一个例子，到时候再具体看一下如何连接。

论文中为了简单起见，在实现中，使用了两个完全随机的树森林（complete-random tree forests）和两个随机森林[Breiman，2001]。每个完全随机的树森林包含1000个完全随机树[Liu et al。，2008]，每棵树通过随机选择一个特征在树的每个节点进行分割实现生成，树一直生长，直到每个叶节点只包含相同类的实例或不超过10个实例。类似地，每个随机森林也包含1000棵树，通过随机选择sqrt(d) 数量的特征作为候选（d是输入特征的数量），然后选择具有最佳 gini 值的特征作为分割。每个森林中的树的数值是一个超参数。

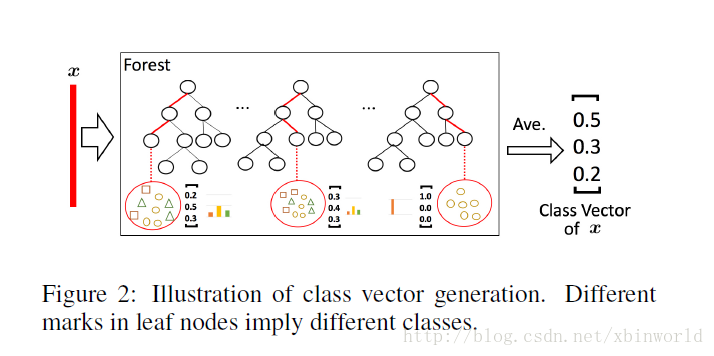
给定一个实例（就是一个样本），每个森林会通过计算在相关实例落入的叶节点处的不同类的训练样本的百分比，然后对森林中的所有树计平均值，以生成对类的分布的估计。如下图所示，其中红色部分突出了每个实例遍历到叶节点的路径。叶节点中的不同标记表示了不同的类。

被估计的类分布形成类向量（class vector），该类向量接着与输入到级联的下一级的原始特征向量相连接。例如，假设有三个类，则四个森林每一个都将产生一个三维的类向量，因此，级联的下一级将接收12 = 3×4个增强特征（augmented feature）。

为了降低过拟合风险，每个森林产生的类向量由k折交叉验证（k-fold cross validation）产生。具体来说，每个实例都将被用作 k -1 次训练数据，产生 k -1 个类向量，然后对其取平均值以产生作为级联中下一级的增强特征的最终类向量。需要注意的是，在扩展一个新的级后，整个级联的性能将在验证集上进行估计，如果没有显着的性能增益，训练过程将终止；因此，级联中级的数量是自动确定的。与模型的复杂性固定的大多数深度神经网络相反，gcForest 能够适当地通过终止训练来决定其模型的复杂度（early stop）。这使得 gcForest 能够适用于不同规模的训练数据，而不局限于大规模训练数据。

（注：级联数量自动确定可以有助于控制模型的复杂性，实际上在每一级的输出结果都用ground truth label来训练的，这里和CNN的理解不同，CNN认为特征是逐层抽象的，而本文在每一层都直接拿label的高层语义来训练——我本人有一些担忧，直接这样的级联会不会使得收益并不能通过级数的加深而放大？比如CNN目前可以做到上百层的net，而这里会自动确定深度，也就是说可能没办法做的很深。希望随着更多人的分析，可以在这一点上给出一些结论）

多粒度扫描（Multi-Grained Scanning）

深度神经网络在处理特征关系方面是强大的，例如，卷积神经网络对图像数据有效，其中原始像素之间的空间关系是关键的。（LeCun et al., 1998; Krizhenvsky et al., 2012），递归神经网络对序列数据有效，其中顺序关系是关键的（Graves et al., 2013; Cho et al.，2014）。受这种认识的启发，我们用多粒度扫描流程来增强级联森林。

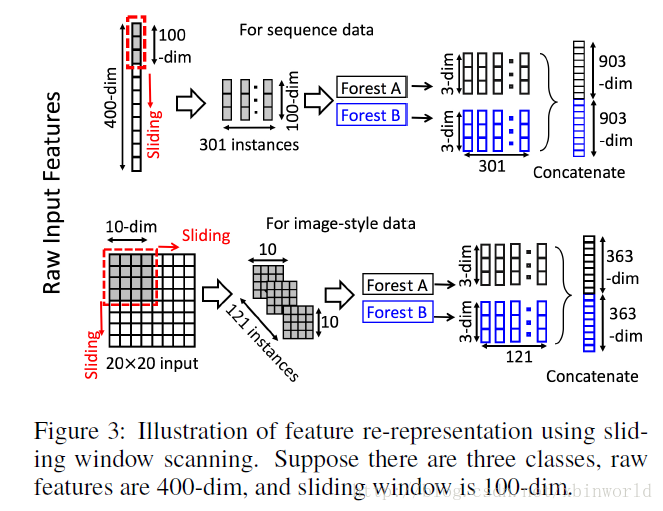
滑动窗口用于扫描原始特征。假设有400个原始特征，并且使用100个特征的窗口大小。对于序列数据，将通过滑动一个特征的窗口来生成100维的特征向量；总共产生301个特征向量。如果原始特征具有空间关系，比如图像像素为400的20×20的面板，则10×10窗口将产生121个特征向量（即121个10×10的面板）。从正/负训练样例中提取的所有特征向量被视为正/负实例；它们将被用于生成类向量：从相同大小的窗口提取的实例将用于训练完全随机树森林和随机森林，然后生成类向量并连接为转换后的像素。如上图的上半部分所示，假设有3个类，并且使用100维的窗口；然后，每个森林产生301个三维类向量，导致对应于原始400维原始特征向量的1,806维变换特征向量。

通过使用多个尺寸的滑动窗口，最终的变换特征矢量将包括更多的特征，如下图所示。

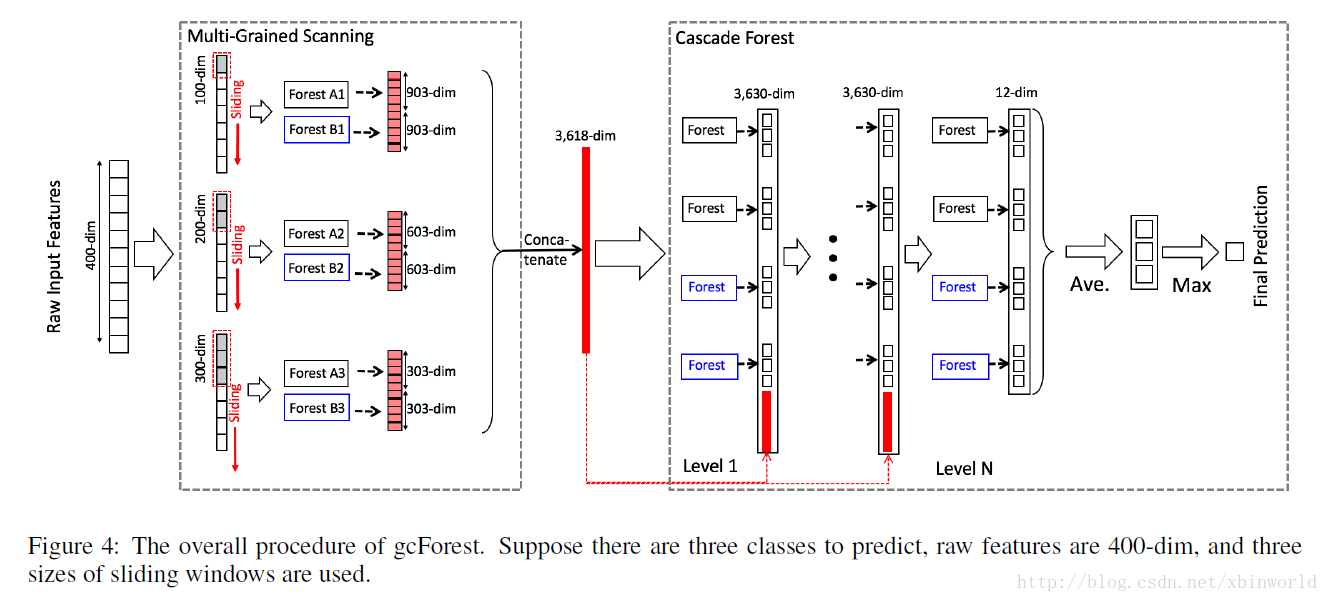
concat成一个3618-dim的原始数据，表示原始的一个数据样本，第一级的输出是12+3618=3630，后面也是一样，直到最后第N级，只有12个输出，然后在每一类别上做avg，然后输出max那一类的label，那就是最终的预测类别。

实验结果

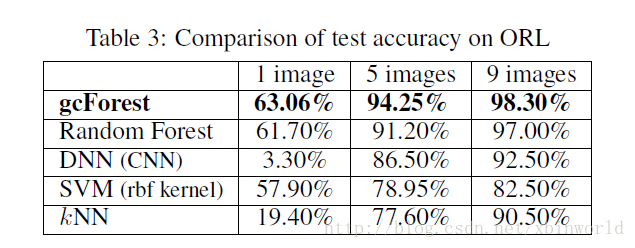
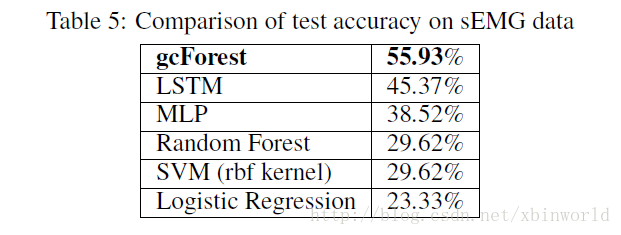
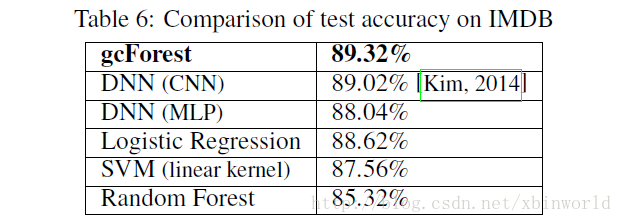
这一部分也是网上大家有疑问的地方，主要是数据集选取都是比较小的实验数据，这个方法能不能火还是要看在real data上能不能做到和DL一样的效果。

下面简单贴几个结果

总结

带着深度学习的关键在于特征学习和巨大模型的能力这一认识，我们在本文中试图赋予树集成这些属性，并提出了 gcForest 方法。与深度神经网络相比，gcForest在我们的实验中表现了极高的竞争力或更好的性能。更重要的是，gcForest 具有少得多的超参数，并且对参数设置不太敏感；实际上在我们的实验中，通过使用相同的参数设置在不同的域中都获得了优异的性能，并且无论是大规模还是小规模的数据，它的工作都很好。此外，作为一种基于树的方法，gcForest 应该比深度神经网络更容易进行理论分析，不过这超出了本文的讨论范围。我们很快会提供 gcForest 的代码。

出自原文[2]：“构建深度森林还存在其他可能性。作为一个会议论文，我们只朝这个方向进行了一点点探索。如果我们有更强大的计算设施，我们想尝试大数据和深度森林，这将留待以后讨论。原则上，深度森林应该能够展示出深度神经网络的其他能力，如充当特征提取器或预训练模型。 值得一提的是，为了解决复杂的任务，学习模型可能需要更深入。然而，当前的深度模型总是神经网络。本文说明了如何构建深度森林，我们相信它是一扇门，可能替代深度神经网络的许多任务。”

这篇文章通俗易懂，要详细了解的话需要对决策树，random forest稍有了解，可以去看一下我前面的博客：机器学习方法(四)：决策树Decision Tree原理与实现技巧 以及 机器学习方法（六）：随机森林Random Forest，bagging；和离散类别特征不同，本文都是基于连续特征为数据特征的，比如像素等等，因此，决策树都是基于连续特征构建的。

仅通过本来说DL算法可取代还为时过早，神经网络有其独特性，而且存在着设计上的美——计算模式统一，端到端，没有过多人文设计；而本文说实话，我还是觉得有很多人为设计的痕迹，希望更多的学者可以在tree based learning method方向上找到更多突破。

参考资料

[1] http://it.sohu.com/20170302/n482153688.shtml 
[2] Deep Forest: Towards An Alternative to Deep Neural Networks, 2017