【刷力扣】23. 合并 K 个升序链表（dummy节点技巧 + 分治思维 + 优先队列）

本文主要是介绍【刷力扣】23. 合并 K 个升序链表（dummy节点技巧 + 分治思维 + 优先队列），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、合并升序链表问题

• 合并升序链表问题是链表专题的经典问题。
  • 我们需要掌握：dummy节点的技巧。
• 23. 合并 K 个升序链表在21. 合并两个有序链表基础上，还需要掌握如下技能：
  • （1）分治思维。我们将合并K个升序链表转化为多次合并2个升序链表。归并排序也用到了分治思维。
  • （2）优先队列（小根堆/大根堆）。维护一个序列的最小/大值。

二、题目：21. 合并两个有序链表

1、掌握dummy节点的技巧

• 在创建新链表时，定义一个dummy节点，在如下代码中，res便是dummy节点，因此，最后答案是：return res.next;

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode mergeTwoLists(ListNode list1, ListNode list2) {if (list1 == null) {return list2;}if (list2 == null) {return list1;}ListNode p1 = list1, p2 = list2, res = new ListNode(), p = res;while (p1 != null && p2 != null) {if (p1.val <= p2.val) {p.next = p1;p1 = p1.next;} else {p.next = p2;p2 = p2.next;}p = p.next;}if (p1 == null) {p.next = p2;}if (p2 == null) {p.next = p1;}return res.next;}
}

三、题目：23. 合并 K 个升序链表

1、分治思维

1.1 插曲

• 看到这道题，首先想到的是合并2个升序链表。p1指向链表list1，p2指向链表list2。关键步骤是：

if (p1.val <= p2.val) {...
} else {...
}

• 很显然，k个升序链表需要想其他办法去求最小值对应的节点。好久没刷算法了。不记得咋求了…（忘记优先队列了，要补上这个技术点）
• 但想到了归并排序。所以，可以将k个升序链表转成2个升序链表的问题。

1.2 代码

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists.length == 0) return null;return merge(lists, 0, lists.length - 1);}private ListNode merge(ListNode[] lists, int i, int j) {if (i == j) {return lists[i];}if (j - i == 1) {// 两条链表的合并return merge2Lists(lists[i], lists[j]);}int mid = ((j - i) >> 1) + i;ListNode leftList = merge(lists, i, mid);ListNode rightList = merge(lists, mid + 1, j);// 两条链表的合并return merge2Lists(leftList, rightList);}private ListNode merge2Lists(ListNode l1, ListNode l2) {ListNode dummy = new ListNode(), p = dummy;while (l1 != null && l2 != null) {if (l1.val <= l2.val) {p.next = l1;l1 = l1.next;} else {p.next = l2;l2 = l2.next;}p = p.next;}if (l1 == null) {p.next = l2;}if (l2 == null) {p.next = l1;}return dummy.next;}
}

1.3 分析这种解法的时空复杂度

1.3.1 时间复杂度

• 图示：4个链表，两两合并的过程。为便于分析，假设每个链表的节点树为a。
  
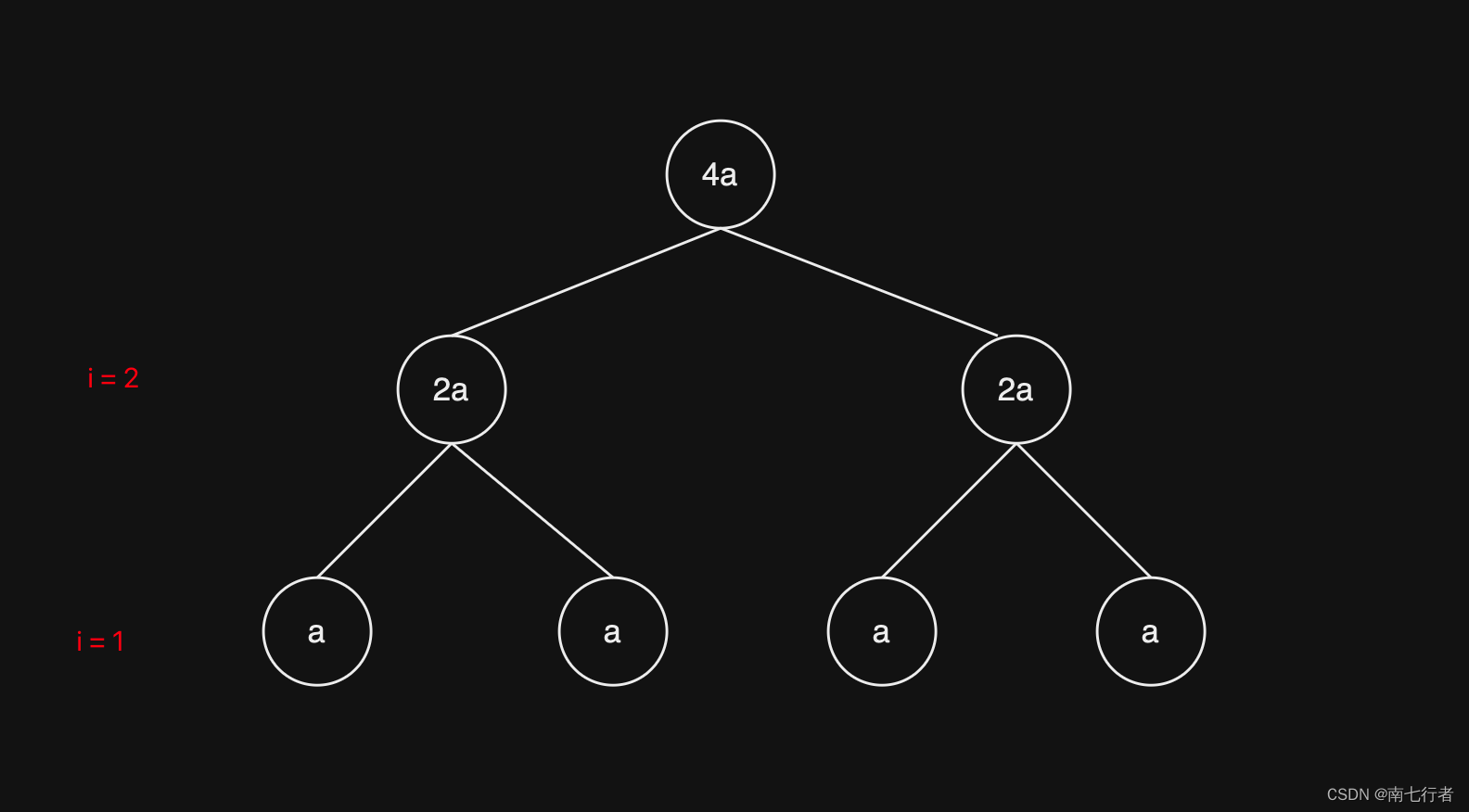
• i = 1：有$\frac{k}{2}$对合并，每对合并涉及2a个节点。
• i = 2：有$\frac{k}{4}$对合并，每对合并涉及4a个节点。
• 每一层的计算：$\frac{k}{2^i}$ * $2^i\ast a$ = $k\ast a$
• 层数为树高：叶子节点为k（k个链表），树高为logk。
• 因此，时间复杂度为：O(aklogk)。k个链表一共有n个节点，所以，a简化为$\frac{n}{k}$，时间复杂度简化为：O(nlogk)

1.3.2 空间复杂度

• 递归调用，栈深度为树高，因此，空间复杂度为O(logk)

2、优先队列

• 给定一组元素，使得队列的头是最小/大元素。

2.1 PriorityQueue的使用

public class Main {public static void main(String[] args) {ListNode listNode1 = new ListNode(2);ListNode listNode2 = new ListNode(1);listNode1.setNext(listNode2);// 小根堆Queue<ListNode> queue = new PriorityQueue<>(Comparator.comparingInt(ListNode::getVal));// 将指定的元素插入到此优先级队列中。（相当于offer()方法）queue.add(listNode1);queue.add(listNode2);while (!queue.isEmpty()) {// 检索并删除此队列的头，如果此队列为空，则返回 null 。System.out.println(queue.poll());}}
}/*
ListNode(val=1, next=null) 
ListNode(val=2, next=ListNode(val=1, next=null))
*/

• 既然要对元素进行排序，要么元素的类实现了Comparable接口（这个要求较高），要么就传入一个自定义的Comparator（这个更灵活）。

2.2 本题代码

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists.length == 0) {return null;}ListNode dummy = new ListNode(), p = dummy;Queue<ListNode> queue = new PriorityQueue<>((node1, node2) -> node1.val - node2.val);for (int i = 0; i < lists.length; i++) {if (lists[i] != null) {ListNode tmp = lists[i];while (tmp != null) {queue.add(tmp);tmp = tmp.next;}}}while (!queue.isEmpty()) {ListNode node = queue.poll();p.next = node;p = p.next;}p.next = null; // 合并升序链表问题，别忘了处理尾节点，否则链表可能成环。return dummy.next;}
}

2.2.1 进一步优化

没必要一次性将所有node都加入优先队列。

class Solution {public ListNode mergeKLists(ListNode[] lists) {if (lists.length == 0) {return null;}ListNode dummy = new ListNode(), p = dummy;Queue<ListNode> queue = new PriorityQueue<>(lists.length, (node1, node2) -> node1.val - node2.val);for (ListNode head : lists) {if (head != null) {queue.offer(head);}}while (!queue.isEmpty()) {ListNode node = queue.poll();p.next = node;p = p.next;if (node.next != null) {queue.offer(node.next);}}p.next = null;return dummy.next;}
}

2.3 分析这种解法的时空复杂度

2.3.1 时间复杂度

• 一个k个链表，总共有n个节点。
• 每个节点都会offer和poll优先队列各一次。
• 每次的时间复杂度为O(logk)：队列中最多k个元素，组成的树高为logk。

我们这里用到的优先队列，本质是小根堆，即一种特殊的完全二叉树。一棵由k个元素组成的完全二叉树，其树高为logk。

• 因此，时间复杂度为O(nlogk)

2.3.2 空间复杂度

• 队列中最多k个元素，因此空间复杂度为O(k)

这篇关于【刷力扣】23. 合并 K 个升序链表（dummy节点技巧 + 分治思维 + 优先队列）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！