本文主要是介绍小而美的算法技巧：前缀和数组，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
小而美的算法技巧：前缀和数组
类似动态规划。
class NumArray {private int[] preSum;public NumArray(int[] nums) {preSum=new int[nums.length+1];//preSum[0]的前缀和为0for(int i=1;i<preSum.length;i++){preSum[i]=nums[i-1]+preSum[i-1];//先计算累加和}}public int sumRange(int left, int right) {return preSum[right+1]-preSum[left];}
}
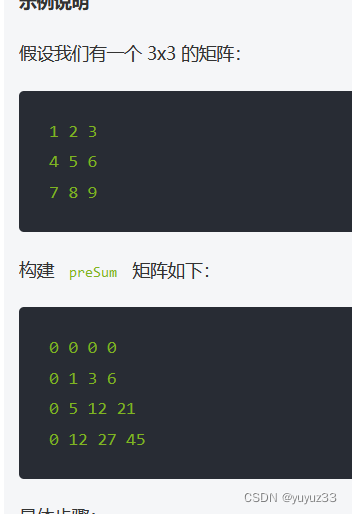
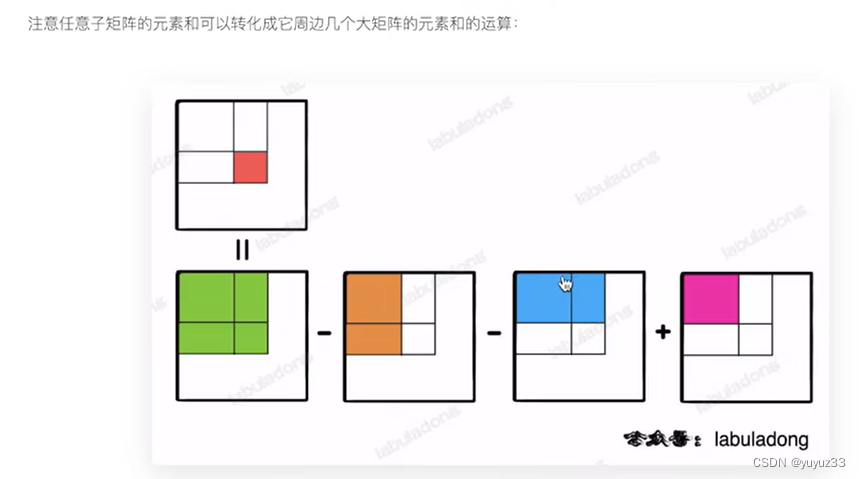前缀和矩阵的构建
我们用 preSum[i][j] 表示从矩阵的左上角 (0,0) 到位置 (i-1,j-1) 这个子矩阵的元素和。为了计算这个值，我们需要考虑以下几个部分的贡献：
- 上方的区域：
- 这是从矩阵的左上角 (0,0) 到位置 (i-2,j-1) 这个子矩阵的元素和，表示为
preSum[i-1][j]。
- 左侧的区域：
- 这是从矩阵的左上角 (0,0) 到位置 (i-1,j-2) 这个子矩阵的元素和，表示为
preSum[i][j-1]。
- 当前位置的元素：
- 这是当前矩阵位置的元素值，表示为
matrix[i-1][j-1]。
- 重复计算的区域：
- 上述两个部分（上方和左侧）的交集部分，即从矩阵的左上角 (0,0) 到位置 (i-2,j-2) 这个子矩阵的元素和，被重复计算了一次，所以需要减去，表示为
preSum[i-1][j-1]。
因此，结合上述四个部分的计算，我们得到：
preSum[i][j] = preSum[i -1][j] + preSum[i][j -1] + matrix[i -1][j -1] - preSum[i -1][j -1];
class NumMatrix {private int[][] preSum;public NumMatrix(int[][] matrix) {int m=matrix.length,n=matrix[0].length;//行列preSum=new int[m+1][n+1];//记录到i-1 j-1的值for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){preSum[i][j]=preSum[i-1][j]+preSum[i][j-1]+matrix[i-1][j-1]-preSum[i-1][j-1];}}}public int sumRegion(int row1, int col1, int row2, int col2) {return preSum[row2+1][col2+1]-preSum[row1][col2+1]-preSum[row2+1][col1]+preSum[row1][col1];}
}/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix obj = new NumMatrix(matrix);* int param_1 = obj.sumRegion(row1,col1,row2,col2);*/差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
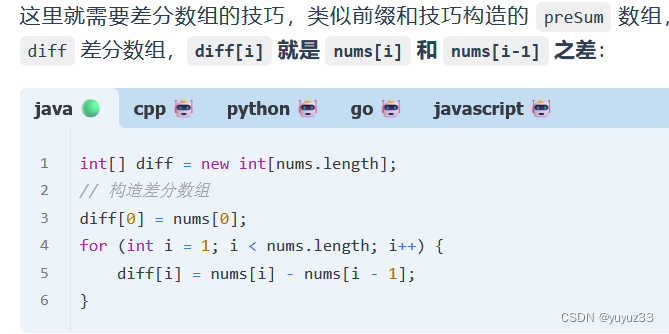
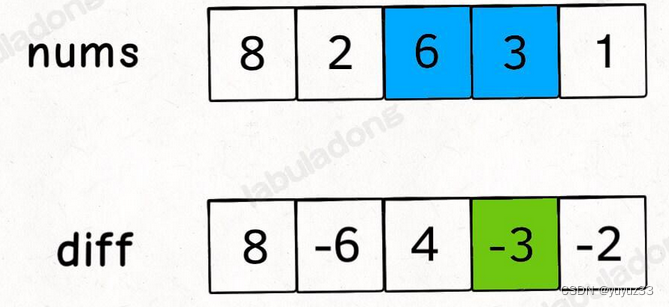
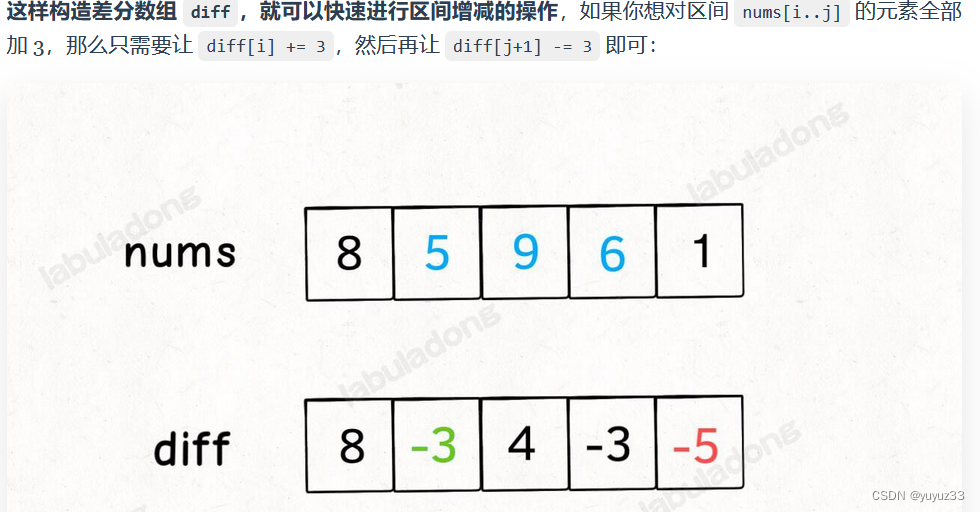
小而美的算法技巧：差分数组
，差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减。
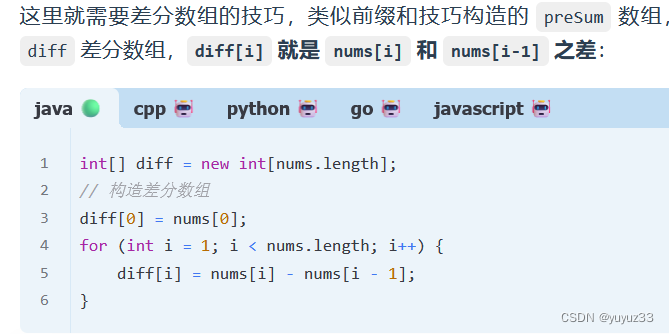
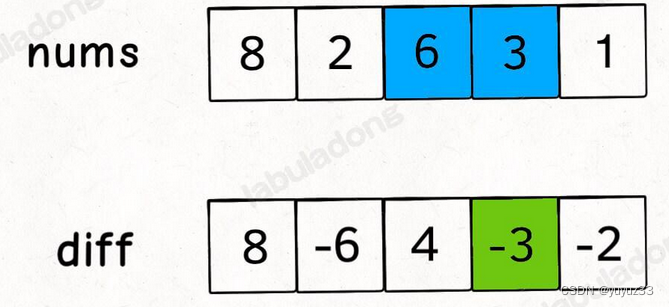
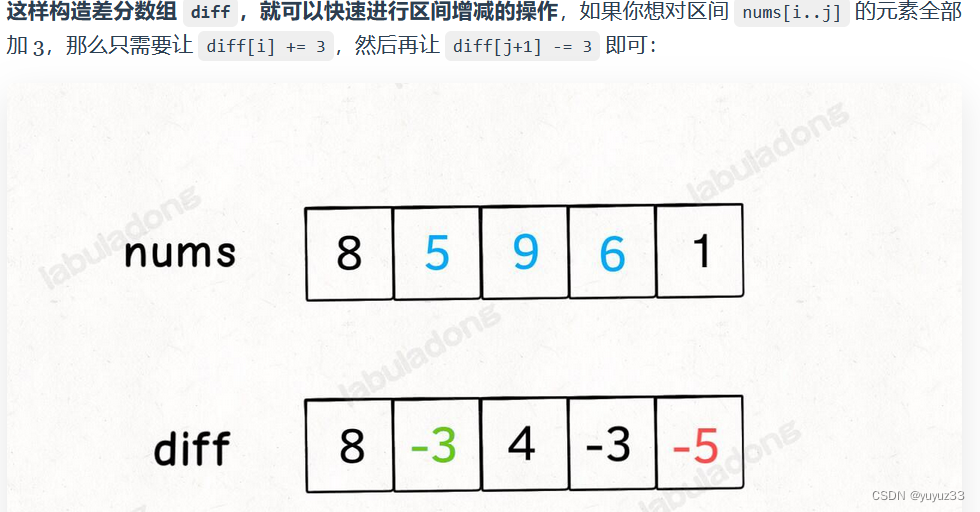
class Solution {public int[] corpFlightBookings(int[][] bookings, int n) {int[] nums=new int[n];//差分方法,只用操作两次for(int[] booking:bookings){nums[booking[0]-1]+=booking[2];//索引从0开始所以-1if(booking[1]<n){nums[booking[1]]-=booking[2];}}for(int i=1;i<n;i++){nums[i]+=nums[i-1];}return nums;}
}
From和to是区间，
class Solution {public boolean carPooling(int[][] trips, int capacity) {int[] dif=new int[1001];for(int[] trip:trips){dif[trip[1]]+=trip[0];dif[trip[2]]-=trip[0];}int cur=0;for(int i=0;i<dif.length;i++){cur+=dif[i];if(cur>capacity) return false;}return true;}
}这篇关于小而美的算法技巧：前缀和数组的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
