本文主要是介绍(3.12)递归与分支之分治,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1.算法的总体思想
- 2.分治法的适用条件
- 3.递归复杂度计算
1.算法的总体思想
- 分治和递归是互不分离的
- (1)将要求解的较大规模的问题分割成k个更小规模的子问题
- (2)对这k个子问题分别求解。如果子问题的规模仍然不够小,则再划分为k个子问题,如此递归的进行下去,直到问题规模足够小,很容易求出其解为止。

- (3)将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来问题的解

- 总结,算法的总体思想是:将求出的小规模的问题的解合并为一个更大规模的问题的解,自底向上逐步求出原来问题的解。
2.分治法的适用条件
-
分治法所能解决的问题一般具有以下几个特征:
-
(1)该问题的规模缩小到一定的程度就可以容易地解决;
因为问题的计算复杂性一般是随着问题规模的增加而增加,因此大部分问题满足这个特征。 -
(2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质
这条特征是应用分治法的前提,它也是大多数问题可以满足的,此特征反映了递归思想的应用 -
(3)利用该问题分解出的子问题的解可以合并为该问题的解;
能否利用分治法完全取决于问题是否具有这条特征,如果具备了前两条特征,而不具备第三条特征,则可以考虑贪心算法或动态规划。 -
(4)该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
这条特征涉及到分治法的效率,如果各子问题是不独立的,则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然也可用分治法,但一般用动态规划较好。 -
分治法的基本步骤
divide-and-conquer(P)
{if ( | P | <= n0) adhoc(P); //解决小规模的问题,问题规模P很小,就直接求解divide P into smaller subinstances P1,P2,...,Pk; //分解问题,分解成k个子问题for (i=1,i<=k,i++)yi=divide-and-conquer(Pi); //递归的解各子问题,第i个问题的解在yi中return merge(y1,...,yk); //将各子问题的解合并为原问题的解
}
- 平衡子问题
使用分治递归,最好使子问题的规模大致相同 - 分治法的复杂性分析
设问题规模足够小的adhoc耗费1个单位时间。
设分解子问题及子问题的解合并需用f(n)个单位时间。
用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间,则有:

3.递归复杂度计算
-
目前的组要方法:代换法,递归树法,主方法
-
求解复杂度需要忽略技术细节:在进行分析时先忽略这些细节,而后再确定其重要与否
(1)假设n 可能是非整数.
(2)忽略掉上取整和下取整,即n/2 可能是非整数.
(3)忽略掉边界条件:
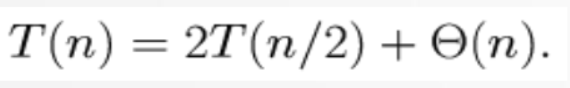

-
(1)代换法
主要思想:1、猜测解的形式;2、 通过数学归纳法找出使解真正有效的常数.
eg:
归并排序计算复杂度的递推关系式为:T(n)=2T(n/2)+n
步骤1:猜测 T(n)=O(n lgn)。原因:问题的规模分成n/2,合并的规模是n,每次分成一半的规模,分的是2个,这样分下去最多分logn趟,每趟最多处理n个数据,所以是O(nlong)的复杂度
步骤2:证明对某一常数c>0,有 T(n)≤cnlgn

结论: 代换法名称来源于当归纳假设用较小的值时,用所猜测的值代替函数的解。这种方法很有效,但只能用于解的形式很容易猜测的情形 -
(3)主方法
T(n) = aT(n/b) + f(n)

eg1:T(n)=9T(n/3)+n求出其四件复杂度
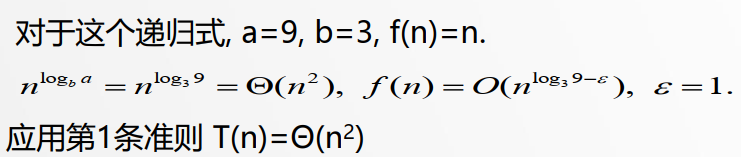
eg2:求解: T(n)=T(2n/3)+1的时间复杂度

这篇关于(3.12)递归与分支之分治的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







