LLama2源码分析——Rotary Position Embedding分析

本文主要是介绍LLama2源码分析——Rotary Position Embedding分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考：一文看懂 LLaMA 中的旋转式位置编码（Rotary Position Embedding）

原理推导参考自上文，以下结合huggingface代码分析公式计算过程

1 旋转角度计算

计算公式如下，其中d为词嵌入维度，这部分和论文原文一样
$\theta_j=10000^{-2(j-1)/d},j\in [1,2,\ldots,d/2]$

# 计算词向量元素两两分组之后，每组元素对应的旋转角度
# 维度：[dim / 2]
inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2).float().to(device) / self.dim))

2 计算整个seq的cos_sin矩阵

def _set_cos_sin_cache(self, seq_len, device, dtype):self.max_seq_len_cached = seq_len# 生成token长度序列t = torch.arange(self.max_seq_len_cached, device=device, dtype=self.inv_freq.dtype)# 计算两个矩阵的外积，结果维度[seq_len, dim // 2]freqs = torch.einsum("i,j->ij", t, self.inv_freq)# 类似[[0, 2, 4, ..., 0, 2, 4, ...], ...]形式，旋转角度两两一组相同emb = torch.cat((freqs, freqs), dim=-1)self.register_buffer("cos_cached", emb.cos().to(dtype), persistent=False)self.register_buffer("sin_cached", emb.sin().to(dtype), persistent=False)

3 计算旋转式位置编码

$\begin{aligned}f_q(x_m,m)&=(W_qx_m)e^{im\theta} \\f_k(x_n,n)&=(W_kx_n)e^{in\theta}\end{aligned}$
公式根据欧拉公式转化后为
$(q_{m}^{(1)}+iq_{m}^{(2)})*(\cos(m\theta)+i\sin(m\theta))$

展开后将结果重新表示为实数向量即为
$q_me^{im\theta}=[q_m^{(1)}\cos(m\theta)-q_m^{(2)}\sin(m\theta),q_m^{(2)}\cos(m\theta)+q_m^{(1)}\sin(m\theta)]$
key的计算同理，以上公式是2维embedding的旋转编码计算，实际代码中是将高纬度的embedding两两分组按照上述公式计算，同一组内的旋转角度相同，此处Llama代码中的分组计算方式与论文原文有所区别，论文原文中是将embedding_dim维度（最后一维）的向量按照相邻两个位置数字为一组，可以按照如下代码理解

>>> a
tensor([[1, 2, 3, 4, 5, 6, 7, 8],[1, 2, 3, 4, 5, 6, 7, 8]])
>>> a.view(2, -1, 2)
tensor([[[1, 2],[3, 4],[5, 6],[7, 8]],[[1, 2],[3, 4],[5, 6],[7, 8]]])

因此，单个token的位置编码是如下图方式计算

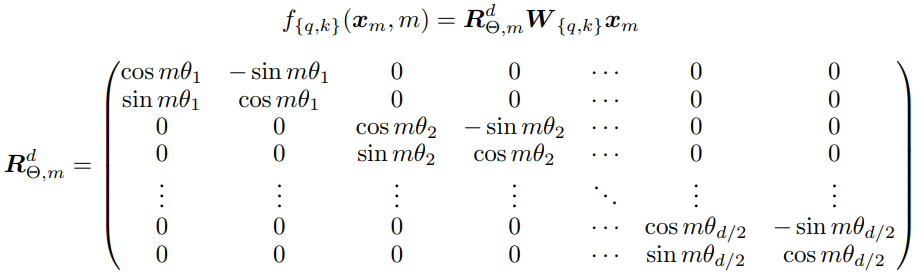
但以上的R矩阵比较稀疏，计算时浪费大量算力，因此Llama中采用不同的方式计算

Llama源码中计算方法

$\begin{pmatrix} {q_0}\\{q_1}\\{\vdots}\\{q_{d/2-1}}\\{q_{d/2}}\\{q_{d/2+1}}\\{\vdots}\\{q_{d-1}} \end{pmatrix} \otimes \begin{pmatrix} \cos m\theta_0\\\cos m\theta_2\\\cos m\theta_4\\\vdots\\\cos m\theta_{d-2}\\\cos m\theta_0\\\cos m\theta_2\\\vdots\\\cos m\theta_{d-2} \end{pmatrix} + \begin{pmatrix} {-q_{d/2}}\\{-q_{d/2+1}}\\\vdots\\{-q_{d-1}}\\{q_{1}}\\{q_{2}}\\\vdots\\{q_{d/2-1}} \end{pmatrix} \otimes \begin{pmatrix} \sin m\theta_0\\\sin m\theta_2\\\sin m\theta_4\\\vdots\\\sin m\theta_{d-2}\\\sin m\theta_0\\\sin m\theta_2\\\vdots\\\sin m\theta_{d-2} \end{pmatrix}$

def rotate_half(x):"""Rotates half the hidden dims of the input."""x1 = x[..., : x.shape[-1] // 2]x2 = x[..., x.shape[-1] // 2 :]return torch.cat((-x2, x1), dim=-1)def apply_rotary_pos_emb(q, k, cos, sin, position_ids, unsqueeze_dim=1):cos = cos[position_ids].unsqueeze(unsqueeze_dim)sin = sin[position_ids].unsqueeze(unsqueeze_dim)q_embed = (q * cos) + (rotate_half(q) * sin)k_embed = (k * cos) + (rotate_half(k) * sin)return q_embed, k_embed