fourier transfrom 傅立叶变换代码实现(matlab语言)

本文主要是介绍fourier transfrom 傅立叶变换代码实现(matlab语言)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

DFT的事情拖了很久了，上个学期就一直纠缠着，始终没有理解，去逸夫楼上课每次下课空教室的时候就喜欢一个人“过瘾”，在黑板上写DFT

的表达式，总想着程序实现。大概那样过了一个月，还是没有理解(智商是硬伤)，这几天看了stanford的视频，老师挺逗的，感觉好像懂了，

于是重新写DFT。在matlab下实现了。。。。

个人觉得<The Scientist and Engineer's Guide to Digital Signal Processing>这本书还是很好的。很值得一看，如果对DSP有兴趣的话。

好吧，开源，上代码：

%% ***************************************************************************************
% code writer ?EOF
% code date : 2014.03.11              2014.03.12 update
% e-mail : jasonleaster@gmail.com
% code purpose : 
%       This code is demo for DFT. I would like to share my code with
%       someone who is interesting in DSP. If there is something wrong with
%       my code, please touche me by e-mail. Thank you!
%
%% ***************************************************************************************TotalSample = 400;
%The number of all the signal that our sensor got
circle = TotalSample/2;
% circle = TotalSample;
%We assume that the preiod of the signal we generated is 'circle';
SignalInS = zeros(circle,1);
%This varible is used for recording the signal in frequency domain
SignalInT = zeros(TotalSample,1);
%This varible is used for recording the signal which were processed by inverse-DFT in time domain
OriginalSignal = zeros(TotalSample,1);
%This varible is used for recording the original signal that we got.%% initialize a square wave
for SampleNumber = -(TotalSample/2):(TotalSample/2)-1if (mod(abs(SampleNumber),circle) < (circle/2))&&(SampleNumber>0)OriginalSignal((TotalSample/2)+1+SampleNumber) = 5;elseif (mod(abs(SampleNumber),circle) >= (circle/2))&&(SampleNumber>0)OriginalSignal((TotalSample/2)+1+SampleNumber) = 0;elseif (mod(abs(SampleNumber),circle) < (circle/2))&&(SampleNumber<0)OriginalSignal((TotalSample/2)+1+SampleNumber) = 0;   elseif (mod(abs(SampleNumber),circle) >= (circle/2))&&(SampleNumber<0)OriginalSignal((TotalSample/2)+1+SampleNumber) = 5;end
end% %% initialize a delta wave
% for SampleNumber = -(TotalSample/2):(TotalSample/2)-1
%     if (SampleNumber == 0)
%         OriginalSignal((TotalSample/2)+1+SampleNumber) = 5;
%     end
% end%We show the original signal in time domain.
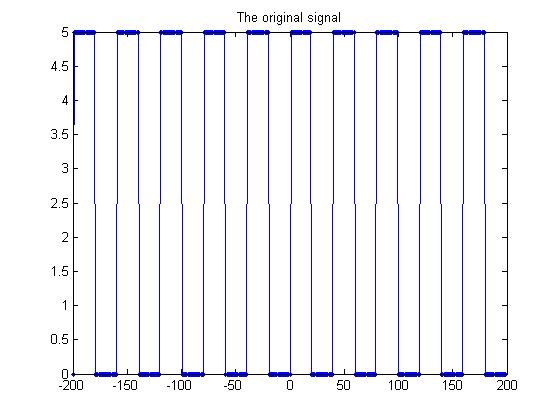
figure(1);
plot( -(TotalSample/2):(TotalSample/2)-1,OriginalSignal,'.-');
title('The original signal');%% forward-DFT
for frequency = -(circle/2):(circle/2)-1 % You must knew what is "Shannon sampling theorem" and you will knew that why frequency is from -(circle/2) to (circle/2)-1for SampleNumber = -(TotalSample/2):(TotalSample/2)-1%Nothingelse, just from 1 to TotalSampleSignalInS((circle/2)+1+frequency) = ...SignalInS((circle/2)+1+frequency) + ...OriginalSignal((TotalSample/2)+1+SampleNumber)*exp(-2*pi*(frequency/circle)*(SampleNumber)*i);end
end%We show the real part of processed signal in frequency domain.
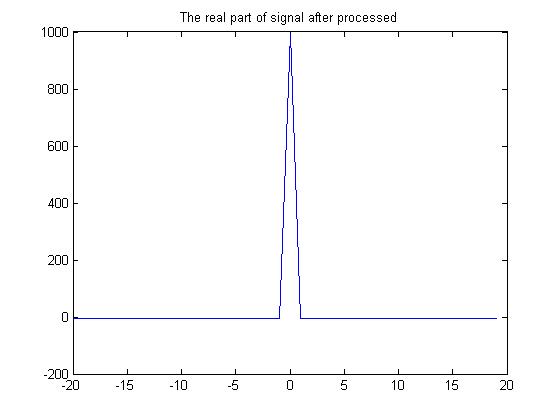
figure(2);
plot(-(circle/2):(circle/2)-1,real(SignalInS),'-');
title('The real part of signal after processed');%We show the imagine part of processed signal in frequency domain.
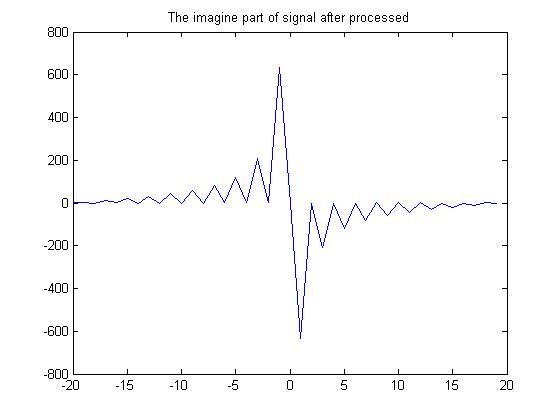
figure(3);
plot(-(circle/2):(circle/2)-1,imag(SignalInS),'-');
title('The imagine part of signal after processed');%% inverse-DFT
for frequency = -(circle/2):(circle/2)-1for SampleNumber = -(TotalSample/2):(TotalSample/2)-1SignalInT((TotalSample/2)+1+SampleNumber) = ...SignalInT((TotalSample/2)+1+SampleNumber) + ...(1/TotalSample)*SignalInS((circle/2)+1+frequency)*exp(2*pi*(frequency/circle)*(SampleNumber)*i);end
end%Just show the signal that we rebuilt by inverse-DFT
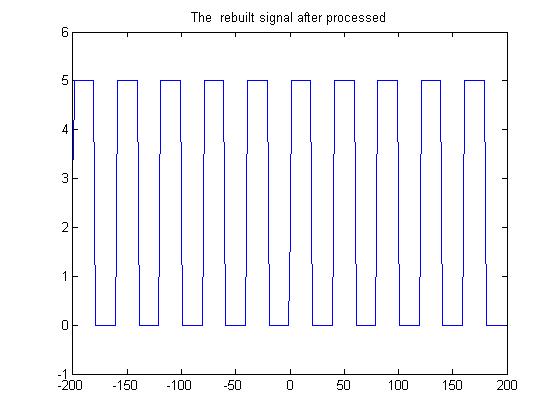
figure(4);
plot(-(TotalSample/2):(TotalSample/2)-1,SignalInT,'-');
title('The  rebuilt signal after processed');

我们假设初始信号是方波信号

处理后的实数部分

处理后的虚数部分

逆变换合成的信号

可以看出逆变换的效果是很好的。

这里应该注意

circle = TotalSample/2;

信号周期不能太短，太短了就会出现aliasing引起的逆向变换误差很大。设置值的时候，根据shannon sampling定理来模拟相应的信号周期就可以了

It is hard and wonderful time when you are thinking about fourier transform.

2014.03.12更新：

原来的代码有点问题，对于delta函数的傅立叶变换显然不正确。现在对代码作出更正

The . L

于XTU

update: 2014.10.29

方波的初始化部分可以用以下算法，使得方波关于ｙ轴对称

%% initialize a square wave
for SampleNumber = -(TotalSample/2):(TotalSample/2)-1if (mod(abs(SampleNumber),circle) <= (circle/4)) || (mod(abs(SampleNumber),circle) > (circle*3/4))OriginalSignal((TotalSample/2)+1+SampleNumber) = 5;elseOriginalSignal((TotalSample/2)+1+SampleNumber) = 0;end
end