基于python下sko.GA的遗产算法解决CVRP（含容量约束的车辆最短路径）问题

本文主要是介绍基于python下sko.GA的遗产算法解决CVRP（含容量约束的车辆最短路径）问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

多vehicle的CVRP看作是one vehicle的CVRP，只是在vehicle自身负载的货物不够时，需要返回depot点
题目如下：
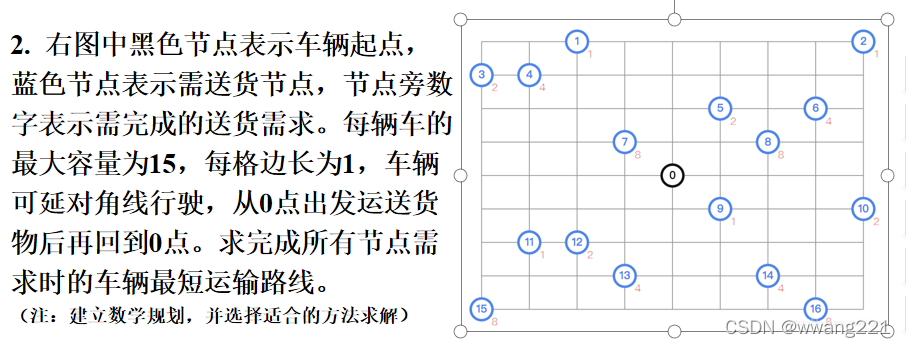
在这里插入图片描述
python代码

from sko.GA import GA_TSP
import matplotlib.pyplot as plt
import numpy as np# 坐标分布情况，（4，4）为补货地点吗
points_coordinate = np.array([[4,4],[2,8],[8,8],[0,7],[1,7],[5,6],[7,6],[3,5],[6,5],[5,3],[8,3],[1,2],[2,2],[3,1],[6,1],[0,0],[7,0]] )
# 除初始点（4，4）以外，每个地点货物需求量
requirements = [1,1,2,4,2,4,8,8,1,2,1,2,4,4,8,8]plt.scatter(*list(zip(*points_coordinate)))
plt.show()

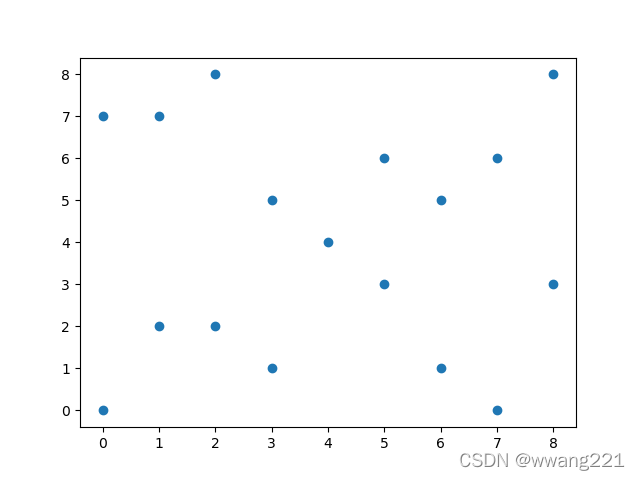
在这里插入图片描述

# 可以将补货行为理解为多车辆单次VRP，总需求/最大载量，最小需要4次
num_vehicle = 4
max_capacity = 15
num_points = len(points_coordinate)
num_customers = num_points - 1
distance_matrix = np.linalg.norm(points_coordinate[:, None, :] - points_coordinate[None, :, :], axis=-1)# 计算总行驶距离：初始点（4，4）到第1路径点+第1路径的到第n路径点再回到初始点
# routine中包含初始点，用于计算车辆回到初始点的距离
def obj_func(routine):num_points, = routine.shapereturn distance_matrix[0, routine[0]] \+ sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)]) \+ distance_matrix[routine[-1], 0]# 增加约束，计算所有超出最大载量的累积数值，当作在计算个体fitness的时候的惩罚
def constraint_capacity(routine):capacity = 0c = 0for i in routine:if i != 0:c += requirements[i-1]else:capacity += max(0, c-max_capacity)c = 0capacity = max(c-max_capacity, capacity)return capacityga_tsp = GA_TSP(func=obj_func, n_dim=num_customers, size_pop=200, max_iter=200, prob_mut=1)# 生产Chrom个体，每个个体代表一个routine
# np.zeros(shape=(ga_tsp.size_pop, num_vehicle-1)：为3次回到初始点（首次出发不算在内）
# ga_tsp.Chrom + 1：为剔除初始点的points_coordinate中的index
ga_tsp.Chrom = np.concatenate([np.zeros(shape=(ga_tsp.size_pop, num_vehicle-1), dtype=int), ga_tsp.Chrom + 1],axis=1)
#添加约束
ga_tsp.has_constraint = True
ga_tsp.constraint_ueq = [constraint_capacity]
best_points, best_distance = ga_tsp.run()
print(best_distance)

画图

fig, ax = plt.subplots(1, 2)
best_points_ = np.concatenate([[0], best_points, [0]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1], 'o-r')
ax[1].plot(ga_tsp.generation_best_Y)
plt.show()