本文主要是介绍罗德里格斯旋转公式证明-简洁,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
罗德里格斯旋转公式证明。
设旋转向量为 ( n , θ ) (n, \theta) (n,θ),设其对应的旋转矩阵为 R R R,
如何证明?
R = c o s θ I + n ∧ s i n θ + ( 1 − c o s θ ) n n T R=cos\theta I + n^{\wedge}sin\theta+(1-cos\theta)nn^{T} R=cosθI+n∧sinθ+(1−cosθ)nnT
证明过程如下:
如图所示,设旋转向量为 A ^ \hat{A} A^,记为 n n n,设三维中的点 r r r绕 n n n旋转 θ \theta θ后得到 r ′ r^{'} r′,其中 n n n为单位方向向量,向量 n n n的起点为坐标原点。
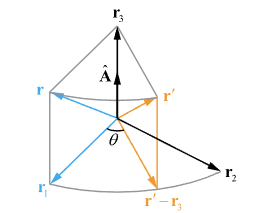
r 3 r_3 r3为r在 n n n上的投影,则
r 3 = ( r ⋅ n ) n (1) r_3=(r\cdot n)n \tag{1} r3=(r⋅n)n(1)
r 1 r_1 r1为r减去r在 n n n上面的分量 r 3 r_3 r3,则
r 1 = r − r 3 (2) r_1=r-r_3 \tag{2} r1=r−r3(2)
r 2 r_2 r2为 n n n与 r 1 r_1 r1的叉乘结果向量,则
r 2 = n × r 1 (3) r_2 = n\times r_1 \tag{3} r2=n×r1(3)
因此, r 1 , r 2 , r 3 r_1,r_2,r_3 r1,r2,r3构成了两两垂直的坐标系,但是模长不等于1, r 1 r_1 r1与 r 2 r_2 r2模长相等。
由上图所示, r ′ r^{'} r′在 r 1 和 r 2 r_1和r_2 r1和r2所在的平面上的投影为 r ′ − r 3 r^{'}-r_3 r′−r3,则将其用 r 1 和 r 2 r_1和r_2 r1和r2表示有
r ′ − r 3 = r 1 c o s θ + r 2 s i n θ r^{'}-r_3=r_1cos\theta+r_2sin\theta r′−r3=r1cosθ+r2sinθ
则,
r ′ = r 1 c o s θ + r 2 s i n θ + r 3 (4) r^{'}=r_1cos\theta+r_2sin\theta+r_3 \tag{4} r′=r1cosθ+r2sinθ+r3(4)
综上所述,将(1)(2)(3)代入(4)式,则
r ′ = ( r − r 3 ) c o s θ + ( n × r 1 ) s i n θ + r 3 = r c o s θ + ( n × r 1 ) s i n θ + ( 1 − c o s θ ) r 3 = r c o s θ + ( n × ( r − r 3 ) ) s i n θ + ( 1 − c o s θ ) r 3 = r c o s θ + ( n × r − n × r 3 ) s i n θ + ( 1 − c o s θ ) r 3 ( 由于 n × r 3 = 0 ) = r c o s θ + n × r s i n θ + ( 1 − c o s θ ) r 3 = r c o s θ + n ∧ s i n θ ⋅ r + ( 1 − c o s θ ) ( r ⋅ n ) n = I c o s θ ⋅ r + n ∧ s i n θ ⋅ r + ( 1 − c o s θ ) n n T ⋅ r (5) \begin{aligned} r^{'} &=(r-r_3)cos\theta+(n\times r_1) sin\theta+r_3 \\ &=rcos\theta+(n\times r_1)sin\theta+(1-cos\theta)r_3 \\ &=rcos\theta+(n\times(r-r_3))sin\theta+(1-cos\theta)r_3 \\ &=rcos\theta+(n\times r-n\times r_3)sin\theta+(1-cos\theta)r_3 \space \space(由于n\times r_3 =0)\\ &=rcos\theta+n\times r sin\theta+(1-cos\theta)r_3 \\ &=rcos\theta+n^{\wedge}sin\theta \cdot r+(1-cos\theta)(r\cdot n)n \\ &=Icos\theta\cdot r+n^{\wedge}sin\theta\cdot r+(1-cos\theta) nn^{T}\cdot r \end{aligned} \tag{5} r′=(r−r3)cosθ+(n×r1)sinθ+r3=rcosθ+(n×r1)sinθ+(1−cosθ)r3=rcosθ+(n×(r−r3))sinθ+(1−cosθ)r3=rcosθ+(n×r−n×r3)sinθ+(1−cosθ)r3 (由于n×r3=0)=rcosθ+n×rsinθ+(1−cosθ)r3=rcosθ+n∧sinθ⋅r+(1−cosθ)(r⋅n)n=Icosθ⋅r+n∧sinθ⋅r+(1−cosθ)nnT⋅r(5)
设旋转矩阵为R,则 r ′ = R ⋅ r r^{'}=R\cdot r r′=R⋅r,由公式(5)可知
R = I c o s θ + n ∧ s i n θ + ( 1 − c o s θ ) n n T R=Icos\theta+n^{\wedge}sin\theta+(1-cos\theta)nn^{T} R=Icosθ+n∧sinθ+(1−cosθ)nnT
证明完毕。
参考链接:
1、https://wuli.wiki/online/RotA.html
2、https://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
3、https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_04_supp.pdf
这篇关于罗德里格斯旋转公式证明-简洁的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







