本文主要是介绍数据结构 | 二叉树（基本概念、性质、遍历、C代码实现），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1.树的基本概念
树是一种 非线性 的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。
把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
有一个特殊的结点，称为根结点，根结点没有前驱结点 除根结点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，
其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继
因此， 树是递归定义 的。
结点的度：一个结点含有的子树的个数称为该结点的度；
叶结点：度为0的结点称为叶结点；
分支结点：度不为0的结点；
父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；
子结点：一个结点含有的子树的根结点称为该结点的子结点；
兄弟结点：具有相同父结点的结点互称为兄弟结点；
树的度：一棵树中，最大的结点的度称为树的度；
结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；
树的高度或深度：树中结点的最大层次；
2.二叉树的基本概念
一棵二叉树是结点的一个有限集合，该集合:
1. 或者为空
2. 由一个根结点加上两棵别称为左子树和右子树的二叉树组成
注意：二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树
2.1特殊的二叉树
满二叉树
一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
完全二叉树
特征：前n-1层都是满的，最后一层可以不满，但最后一层从左到右必须是连续的。
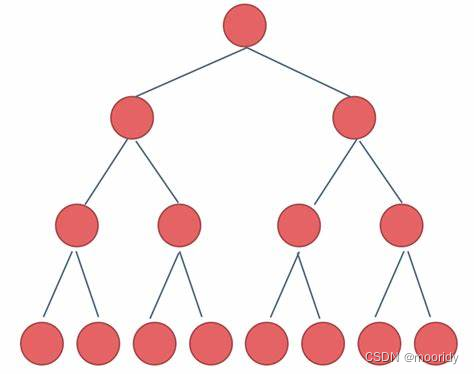
ps: 满二叉树是一种特殊的完全二叉树。
3.二叉树的性质
1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个结点.
2. 若规定根结点的层数为1，则深度为h的二叉树的最大结点数是2^h-1
3. 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有 n0＝n2 ＋1
4. 若规定根结点的层数为1，具有n个结点的满二叉树的深度，h=log2(n+1)
5. 对于完全二叉树:
双亲序号：(i-1)/2 (i为子节点序号）
左孩子序号：2i+1 （i为双亲结点序号）
右孩子序号：2i+2 （i为双亲结点序号）
练习：一个具有767个结点的完全二叉树，其叶子结点个数为（）
A 383
B 384
C 385
D 386
答案：B
详解：设有度为2节点n2个， 度为1节点n1个，度为0节点n0个,
767=n2+n1+n0
n2=n0-1
由上面两式可得：
767=n1+2n0-1
768=n1+2n0
由于2n0必为偶数，768为偶数，可得：n1为偶数
且完全二叉树中n1只能是1或0
因此n1=0
768=2n0
n0=384
4 .二叉树的存储结构
二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。
1. 顺序存储
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空 间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。
2.链式存储
二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。链式结构又分为二叉链和三叉链。本文主要针对二叉链。
5.二叉树的遍历
5.1 前序、中序以及后序遍历
1. 前序遍历——根节点 左子树 右子树
2. 中序遍历——左子树 根节点 右子树
3. 后序遍历——左子树 右子树 根节点
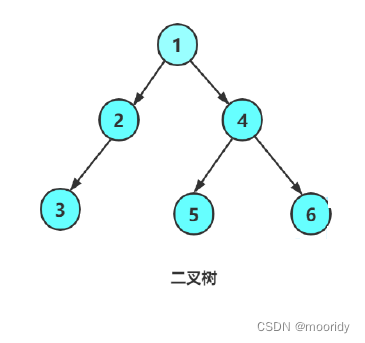
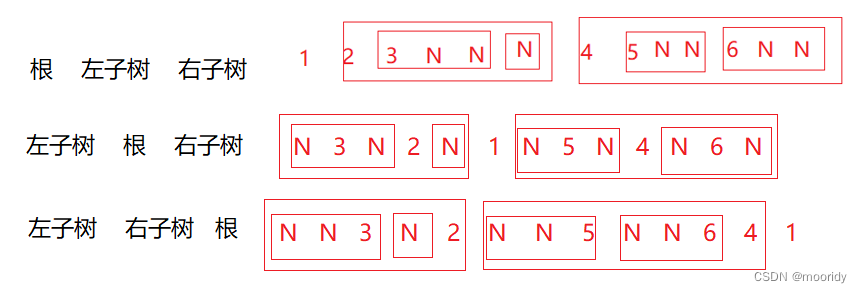
5.2 层序遍历
层序遍历：一层一层地往下遍历
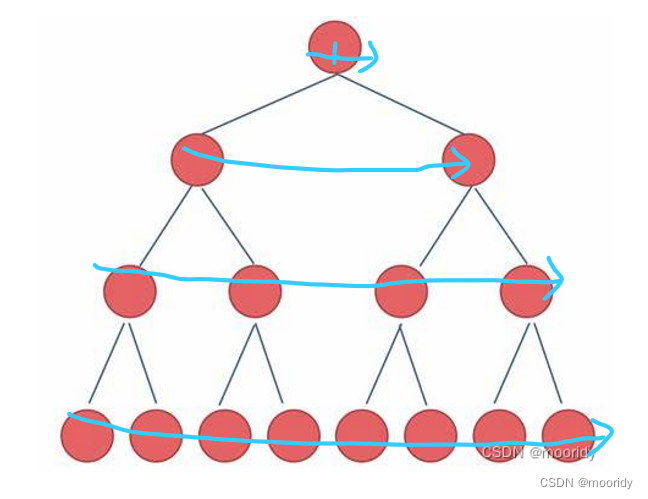
6.二叉树代码实现
思路
前序/中序/后序遍历
递归思想：将当前的大问题拆解成小问题
以前序遍历为例：
当前问题——打印根，打印左子树，打印右子树
子问题——如图
递归返回条件——root==NULL
前序遍历代码
//前序遍历 根节点 左节点 右节点
void BinaryTreePrevOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}中序遍历代码
void BinaryTreeInOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}后序遍历代码
void BinaryTreePostOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}节点个数/叶子节点个数/树高/第k层叶子数
1.节点个数
递归思想：
情况1：空，0个
情况2：不为空，左子树+右子树+1
2.叶子节点个数
情况1：空，返回0
情况2：只有一个结点，返回1
情况3：左子树+右子树
3.树的高度
情况1：空，返回0
情况2：左子树和右子树高度中大的值+1
4.第k层叶子数
情况1：空，返回0
情况2：非空，k==1，返回1
情况3：非空,k>1,左子树第k-1层+右子树第k-1层
int BinaryTreeSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;}int BinaryTreeLeafSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}int BinaryTreeLevelKSize(BTNode* root, int k) {if (root == NULL) {return 0;}if (k==1) {return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}查找值为x的节点
递归思想
情况1：空，返回NULL
情况2：不为空，根值为x，返回根节点
情况3：不为空，根值不为x，查找左子树，有则返回
左子树中无，查找右子树，有则返回
右子树中也无，返回空
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {BTNode* ret = NULL;if (root == NULL) {return NULL;}if (root->data == x) {ret = root;return ret;}if (BinaryTreeFind(root->left, x) != NULL) {ret = BinaryTreeFind(root->left, x);}if (BinaryTreeFind(root->right, x) != NULL) {ret = BinaryTreeFind(root->right, x);}
}
层序遍历/完全二叉树
层序遍历
1.根进队列
2.节点出队列时，该节点的子节点（非空）进队列
3.当队列为空时，循环结束
完全二叉树
1.进行层序遍历，空也进队列
2.遇到第一个空节点，开始判断，后面全空就是完全二叉树，后面有非空就不是完全二叉树
void BinaryTreeLevelOrder(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head->left) {QueuePush(&q, head->left);}if (head->right) {QueuePush(&q, head->right);}printf("%d", head->data);QueuePop(&q);}QueueDestroy(&q);
}bool BinaryTreeComplete(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head == NULL) {break;}QueuePush(&q, head->left);QueuePush(&q, head->right);QueuePop(&q);}while(!QueueEmpty(&q)){BTNode* head = QueueFront(&q);if (head) {QueueDestroy(&q);return false;}QueuePop(&q);}QueueDestroy(&q);return true;
}代码汇总
binarytree.h
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate();
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);
binarytree.c
#define _CRT_SECURE_NO_WARNINGS
#include "binarytree.h"
#include "queue.h"BTNode* BuyNode(BTDataType x) {BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL) {perror("malloc fail!");}newnode->left = NULL;newnode->right = NULL;newnode->data = x;return newnode;
}BTNode* BinaryTreeCreate() {BTNode* Node1 = BuyNode(1);BTNode* Node2 = BuyNode(2);BTNode* Node3 = BuyNode(3);BTNode* Node4 = BuyNode(4);BTNode* Node5 = BuyNode(5);BTNode* Node6 = BuyNode(6);BTNode* Node7 = BuyNode(7);Node1->left = Node2;Node1->right = Node3;Node2->left = Node4;Node2->right = Node5;Node3->left = Node6;//Node6->left = Node7;return Node1;//返回根节点
}
//前序遍历 根节点 左节点 右节点
void BinaryTreePrevOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}void BinaryTreeInOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}void BinaryTreePostOrder(BTNode* root) {if (root == NULL) {printf("N ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}int BinaryTreeSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right)+1;}int BinaryTreeLeafSize(BTNode* root) {if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL) {return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}int BinaryTreeLevelKSize(BTNode* root, int k) {if (root == NULL) {return 0;}if (k==1) {return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ?leftHeight + 1 : rightHeight + 1;
}BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {BTNode* ret = NULL;if (root == NULL) {return NULL;}if (root->data == x) {ret = root;return ret;}if (BinaryTreeFind(root->left, x) != NULL) {ret = BinaryTreeFind(root->left, x);}if (BinaryTreeFind(root->right, x) != NULL) {ret = BinaryTreeFind(root->right, x);}
}void BinaryTreeLevelOrder(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head->left) {QueuePush(&q, head->left);}if (head->right) {QueuePush(&q, head->right);}printf("%d", head->data);QueuePop(&q);}QueueDestroy(&q);
}bool BinaryTreeComplete(BTNode* root) {if (!root) {return;}Queue q;QueueInit(&q);QueuePush(&q, root);while (QueueSize(&q) > 0) {BTNode* head = QueueFront(&q);if (head == NULL) {break;}QueuePush(&q, head->left);QueuePush(&q, head->right);QueuePop(&q);}while(!QueueEmpty(&q)){BTNode* head = QueueFront(&q);if (head) {QueueDestroy(&q);return false;}QueuePop(&q);}QueueDestroy(&q);return true;
}void BinaryTreeDestory(BTNode* root) {if (root==NULL) {return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}在实现层序遍历时，会使用到队列。但由于C语言中没有现成的数据结构队列可以直接使用，需要自己实现。
queue.h
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
typedef struct BinaryTreeNode* QDataType;typedef struct QListNode{struct QListNode* next;QDataType data;
}QNode;// 队列的结构
typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);queue.c
#define _CRT_SECURE_NO_WARNINGS
#include "queue.h"
// 初始化队列
void QueueInit(Queue* q) {assert(q);q->phead = q->ptail = NULL;q->size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data) {assert(q);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL) {perror("malloc fail!");exit(1);}else {newnode->data = data;newnode->next = NULL;if (q->ptail == NULL) {q->phead = q->ptail = newnode;q->size++;}else {q->ptail->next =newnode;q->ptail = newnode;q->size++;}}
}
// 队头出队列
void QueuePop(Queue* q) {assert(q);assert(q->size != 0);if (q->phead->next == NULL) {free(q->ptail);q->ptail = q->phead = NULL;q->size--;}else {QNode* next = q->phead->next;free(q->phead);q->phead = next;q->size--;}
}
// 获取队列头部元素
QDataType QueueFront(Queue* q) {assert(q);assert(q->size > 0);return q->phead->data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q) {assert(q);assert(q->size > 0);return q->ptail->data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q) {assert(q);return q->size;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
int QueueEmpty(Queue* q) {assert(q);return !QueueSize(q);
}
// 销毁队列
void QueueDestroy(Queue* q) {assert(q);while (q->size) {QueuePop(q);}q->phead = NULL;q->ptail = NULL;
}7.堆及堆排序及TopK问题
详见我的另一篇文章~（TopK问题待更）
数据结构 | 详解二叉树——堆与堆排序
这篇关于数据结构 | 二叉树（基本概念、性质、遍历、C代码实现）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
