032.最长有效括号

本文主要是介绍032.最长有效括号，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题意

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

难度

困难

示例

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"

分析

我们利用了栈这个数据结构，当遇到一个右括号，就看一看栈内有没有与之匹配的左括号，如果栈为空或者说栈顶的左括号与之不匹配（除了小括号()还有中括号[]和大括号{}），那么它就不是一个有效的括号序列。

先来回顾一下栈的基本操作：

stack.push(-1); // 入栈
stack.pop(); // 出栈
stack.peek(); // 查看栈顶元素

接下来，我们需要搞清楚最长有效括号子串的特点：

每一个左括号 '(' 都有一个对应的右括号 ')'。
括号之间的嵌套关系是正确的，比如说 (()())、((()))、()()()。

然后，我们需要解决如何得出最长有效括号子串的长度。

新建一个栈，用来存放括号的下标。由于下标是从 0 开始的，我们可以在栈中放入一个 -1，表示栈底，这样更方便计算边界条件。

比如说对于 ()，初始状态是 [-1]，遇到左括号 (，我们将它的下标压入栈中，此时栈内是 [-1,0]。

遇到右括号 )，我们将栈顶的元素弹出，此时栈内是 [-1]，说明是一个有效的括号子串，长度为右括号的下标减去栈顶元素的下标 1 - (-1)，即为 2。

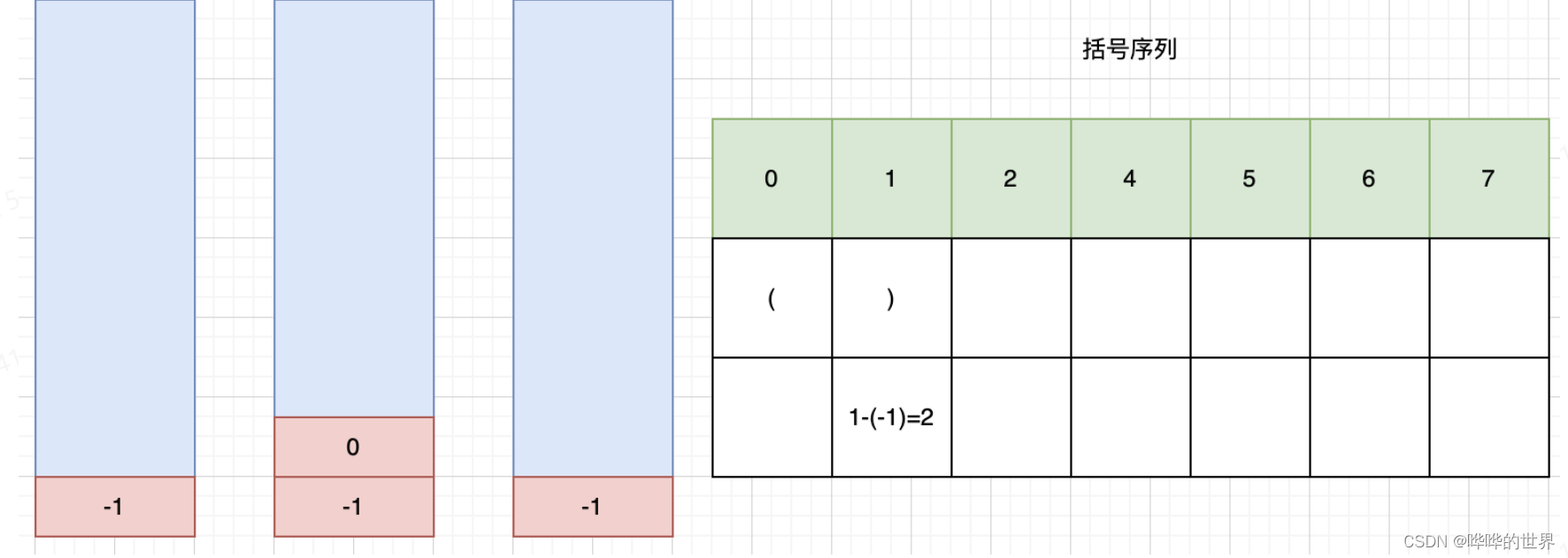
遍历字符串，遇到左括号 (，将它的下标压入栈中；当遇到右括号时，将栈顶的元素弹出，此时有两种情况：

如果栈为空，说明当前的右括号没有与之匹配的左括号，我们将当前的右括号的下标压入栈中
如果栈不为空，说明当前的右括号与栈顶的左括号匹配，我们计算当前的右括号与栈顶的左括号的下标之差，即为当前的有效括号子串的长度

具体代码实现：

public class LongestValidParentheses {public static void main(String[] args) {String s = "(()))())(";LongestValidParentheses longestValidParentheses = new LongestValidParentheses();int res = longestValidParentheses.longestValidParentheses(s);System.out.println("括号有效长度为"+res);}/*** 计算有效括号的字符串* @param s* @return*/public  int longestValidParentheses(String s){int res = 0;  //用于记录有效括号的长度//deque<Integer> deque = new deque<>();  //栈用于括号索引ArrayDeque<Integer> deque = new ArrayDeque<>();deque.push(-1);  //初始化栈 ，放入一个初始值-1//遍历字符串，遇到左括号，将其下标索引加入栈中，遇到右括号，将其栈顶元素弹出// 如果栈为空，说明当前的右括号没有与之匹配的左括号，我们将当前的右括号的下标压入栈中// 如果栈不为空，说明当前的右括号与栈顶的左括号匹配，// 我们计算当前的右括号与栈顶的左括号的下标之差，即为当前的有效括号子串的长度for (int i = 0; i < s.length(); i++) {if (s.charAt(i) == '('){  //如果遇到左括号 ，将其下标加入栈中deque.push(i);}else {deque.pop();  //否则遇到右括号 ，将其栈顶元素弹出if (deque.isEmpty()){//如果栈为空，没有与之匹配的左括号。将当前的下标压入栈中deque.push(i);}else {//如果栈不为空，说明当前的右括号与栈顶的左括号匹配，//计算当前的右括号与栈顶的左括号的下标之差，即为当前的有效括号子串的长度res = Math.max(res, i - deque.peek()); // 计算有效括号长度，并更新最大值}}}return res; // 返回最长有效括号长度}}

假设字符串为 s = "(()))())("，我们来模拟一下整个题解过程：

①、初始化栈 sta = [-1]

②、遍历字符串：

i = 0, s.charAt(i) = '('，将索引 0 压入栈，sta = [-1, 0]

i = 1, s.charAt(i) = '('，将索引 1 压入栈，sta = [-1, 0, 1]

i = 2, s.charAt(i) = ')'，弹出栈顶元素 1，栈不为空，计算长度 2 - 0 = 2，更新 ans = 2

i = 3, s.charAt(i) = ')'，弹出栈顶元素 0，栈不为空，计算长度 3 - (-1) = 4，更新 ans = 4

i = 4, s.charAt(i) = ')'，弹出栈顶元素 -1，栈为空，将索引 4 压入栈，sta = [4]

i = 5, s.charAt(i) = '('，将索引 5 压入栈，sta = [4, 5]

i = 6, s.charAt(i) = ')'，弹出栈顶元素 5，栈不为空，计算长度 6 - 4 = 2，ans = 4（不变）

i = 7, s.charAt(i) = ')'，弹出栈顶元素 4，栈为空，将索引 7 压入栈，sta = [7]

i = 8, s.charAt(i) = '('，将索引 8 压入栈，sta = [7, 8]