本文主要是介绍扎气球最高分-第13届蓝桥杯选拔赛Python真题精选,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第74讲。
扎气球最高分,本题是2021年11月27日举办的第13届蓝桥杯青少组Python编程选拔赛真题编程部分第5题。题目要求对于给定的n个排成一排的气球,将所有气球扎破能够得到的最高分数。
先来看看题目的要求吧。
一.题目说明
编程实现:
小明去游乐场玩飞镖扎气球的游戏,一共有n个气球,依次排成一行,每个气球上有一个数字,表示这个气球的分值。
游戏计分规则:
1、戳破1个气球,将获得其本身及左右相邻气球,共三个分值相乘的分数;
2、如果戳破的气球左边或右边没有气球,则获得其本身及相邻气球,共两个分值相乘的分数;如果被戳破的气球左边和右边都没有气球(是最后一个被戳破的气球),则这个气球本身的分值作为分数;
3、已经被戳破的气球不再计算。
飞镖数量不限,可以任意选择顺序戳破气球,根据计分规则,争取使得游戏最后得分最高。
例如:一共有3个气球,分值分别为2,4,6。
若想获得最高得分:
1). 先戳破4,得分为2 x 4 x 6 = 48;
2). 再戳破2,得分为2 x 6 = 12,累计得分60;
3). 再戳破6,得分为6,累计得分66;
最后总得分为66,为最高得分。
输入描述:
输入n个正整数,表示气球的分值,且正整数之间以一个英文逗号隔开
输出描述:
输出正整数,表示戳破所有气球后获得的最高得分
样例输入:
2,4,6
样例输出:
66
二.思路分析
这是一道动态规划算法题,涉及的知识点包括循环、列表和动态规划等。
这是一个求最值问题,对于最值问题,常见的实现方案有枚举算法、贪心算法、递归算法、回溯算法和动态规划等。
那么你知道本题属于哪种类型呢?
实际上,这是典型的区间DP问题,区间DP问题通常涉及一个列表或数组,需要对其某些子区间进行操作,并通过这些操作的结果来求解整个列表或数组的某些性质或最优值。
区间DP的基本思想是通过定义二维的DP状态数组dp[i][j],表示从序列的第i个元素到第j个元素(即区间[i, j]的最优解,例如最小/最大的某个值)。然后,通过考虑如何将大区间分解成较小的区间,并利用这些较小区间的最优解来构造大区间的最优解,来进行状态转移。
对于动态规划问题,核心点有如下4个:
-
定义dp数组
-
初始状态
-
状态转移方程
-
遍历顺序
接下来,我们逐一分析这4个核心要素。
1. 定义dp数组
由于这是一个区间DP问题,因此dp数组是一个二维列表,即dp[i][j],表示扎破从i到j之间所有的气球的最高得分。
此时,有一个问题需要明确,这里的i和j是否也包含呢?
我们看一组实际的数据,假设有4个气球,分值为3, 2, 4, 6,如图:

在计算最高分的时候,还需要考虑气球是否处于最左边和最右边,代码比较繁琐。
可以考虑在左右两边增加两个虚拟气球,其分值为1,如图:

如此一来,所有的黄色气球都处于中间位置,再也不需要考虑边界问题了。
当然,这也让我们进一步明确了dp[i][j]的含义,它表示的是扎破i到j之间所有气球的最高得分。
对于上面的4个气球来说,最后的结果是dp[0][5],表示从0~5之间所有的气球,不包括0和5本身,因为这两个气球是虚拟的,根本不存在。
可以绘制表格如下:
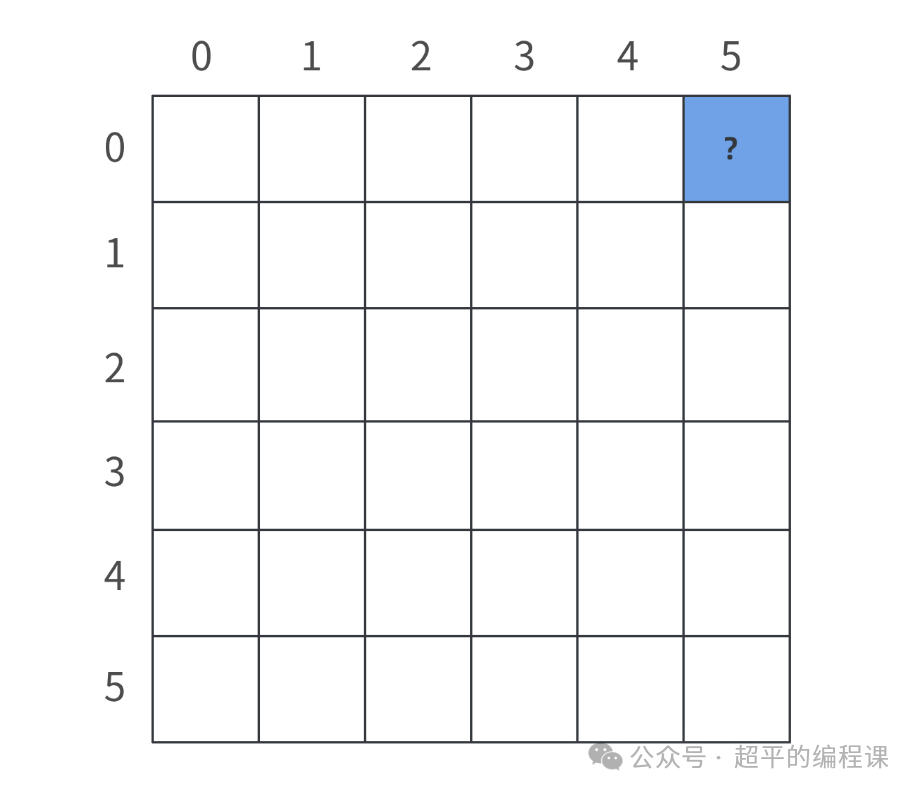
最右上角的单元格dp[0][5]就是最终要计算的结果,实际上,所谓的动态规划,其实就是一个填表的过程。
2. 初始状态
所谓初始状态就是最简单的情况,对于戳气球问题而言,最简单的情况就是没有气球,此时得分为0。
对应到dp[i][j]数组,就是当j - i <= 1,即i和j两者之间没有气球可扎了,当然也就没有分数了。
对应的dp表格如下:
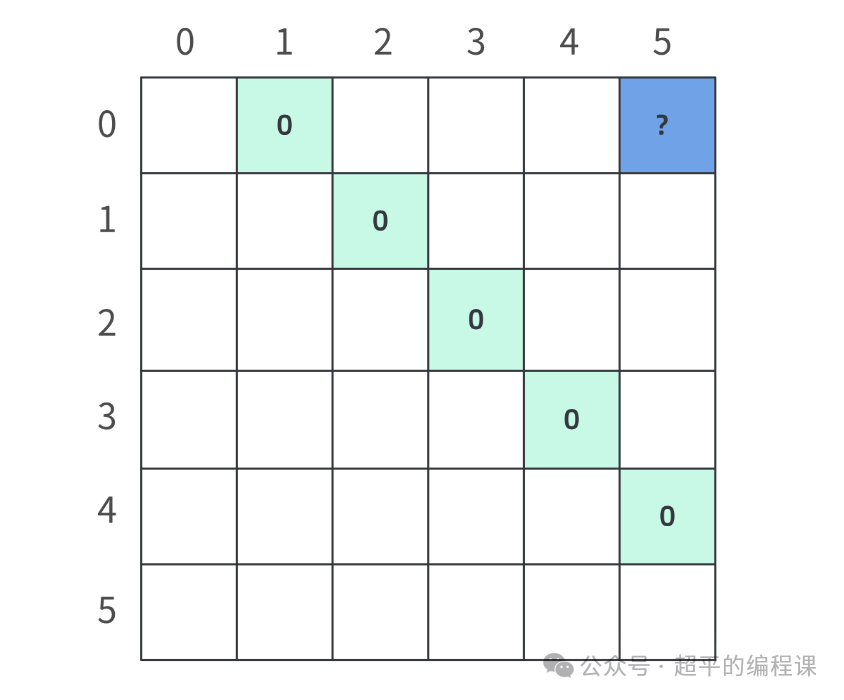
这里将处在对角线偏右上的单元格设置为0,即:
dp[0][1] = dp[1][2] = dp[2][3] = dp[3][4] = dp[4][5]= 0对于dp表格,我们要计算的是右上方的单元格,左下方的单元格可以忽略不计。
3. 状态转移方程
对于动态规划问题,状态转移方程是重点,也是难点,这里的状态转移方程又该如何确定呢?
还是以上面的数据为例,我们只需要分析最后戳破哪个气球的过程,4只气球可以分四种情况来考虑。
1). 最后戳第一只气球
最后戳破的气球分值为3,如图所示:

这相当于把dp[0][5]拆分成两个子区间,分别是dp[0][1]和dp[1][5],戳破当前气球的得分为1 * 3 * 1,所以:
dp[0][5]= dp[0][1] + dp[1][5] + 32). 最后戳第二只气球
最后戳破的气球分值为2,如图所示:

这相当于把dp[0][5]拆分成两个子区间,分别是dp[0][2]和dp[2][5],戳破当前气球的得分为1 * 2 * 1,所以:
dp[0][5]= dp[0][2] + dp[2][5] + 23). 最后戳第三只气球
最后戳破的气球分值为4,如图所示:
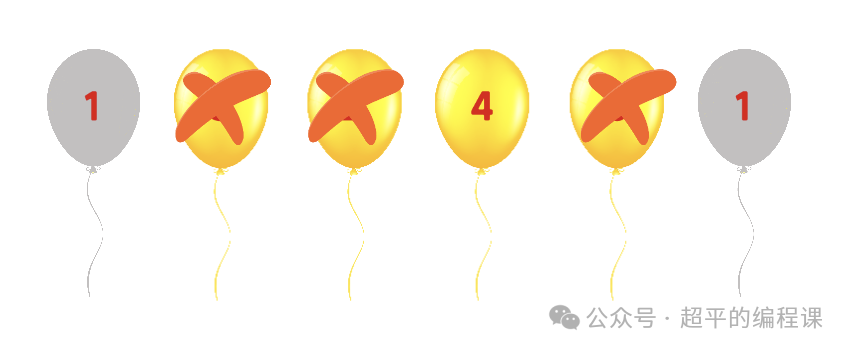
这相当于把dp[0][5]拆分成两个子区间,分别是dp[0][3]和dp[3][5],戳破当前气球的得分为1 * 4 * 1,所以:
dp[0][5]= dp[0][3] + dp[3][5] + 44). 最后戳第四只气球
最后戳破的气球分值为6,如图所示:

这相当于把dp[0][5]拆分成两个子区间,分别是dp[0][4]和dp[4][5],戳破当前气球的得分为1 * 6 * 1,所以:
dp[0][5]= dp[0][4] + dp[4][5] + 6到底哪一种情况得分最高呢,其实就是取最大值的问题了。
你看到这其中的规律了吗?
实际上就是在i和j之间找分割点k,将dp[i][j]拆分成两个子区间dp[i][k]和dp[k][j],如图所示:
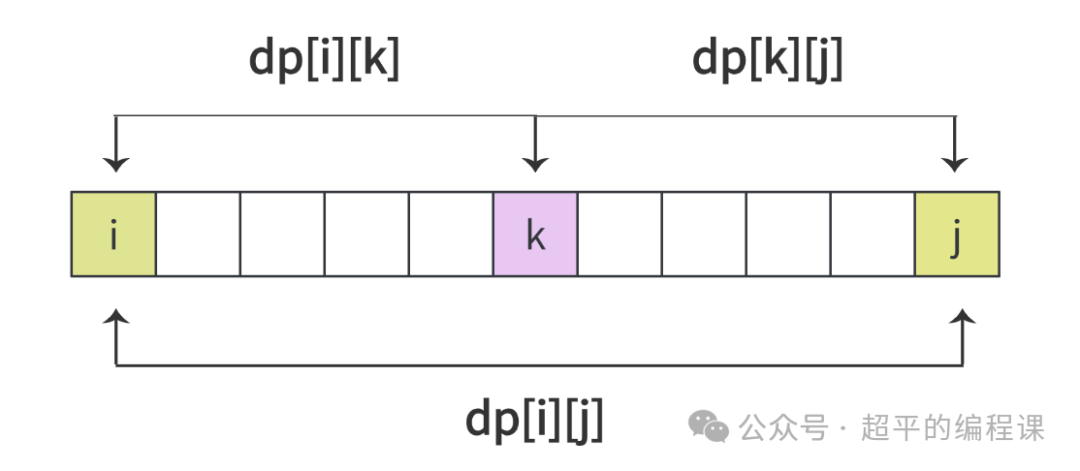
对于每个分割点来说,左边区间的最大分值是dp[i][k],右边区间的最大分值是dp[k][j],加上本次戳破气球的分数p[i] * p[k] * p[j],这里的列表p保存的是每个气球的分值,包括左右两端的虚拟气球。
因此,状态转移方程如下:
dp[i][j] = max(dp[i][j],dp[i][k] + dp[k][j] + p[i] * p[j] * p[k])
这意味着,我们需要使用循环枚举i到j之间的每个分割点k,计算其最大分值,然后将最大值作为dp[i][j]的结果。
4. 遍历顺序
对于二维列表dp[i][j]来说,常见的遍历顺序是从上到下,从左到右。但是对于区间DP来说,不能采取这种遍历顺序。
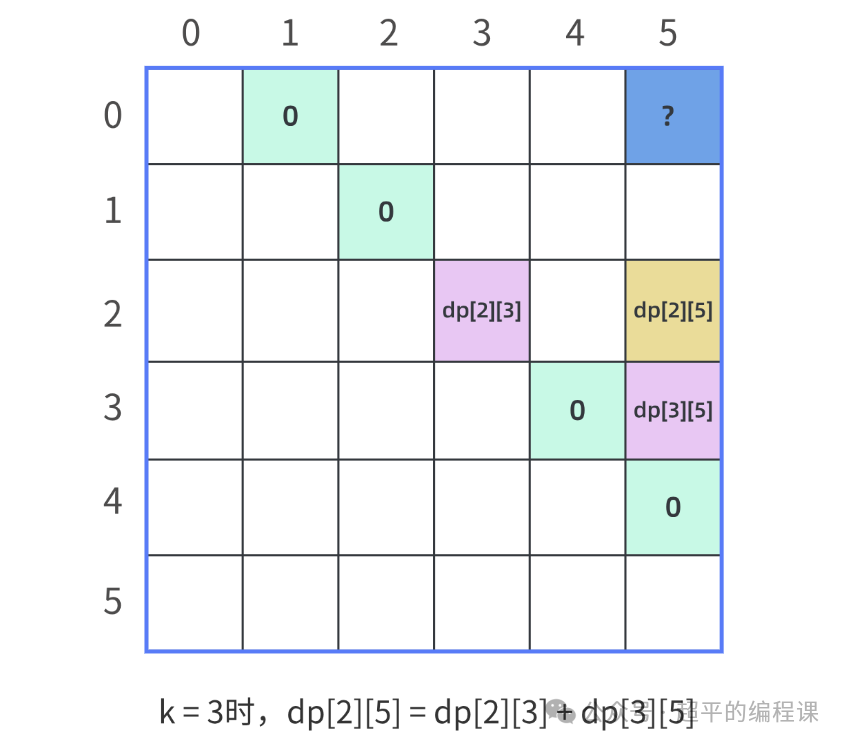
我们还是看图说话吧,以计算dp[2][5]为例,它的分割点k有两个。
当k = 3时,计算如下:
dp[2][5] = dp[2][3] + dp[3][5] + p[2]* p[3] * p[5]对应的DP表格如图:
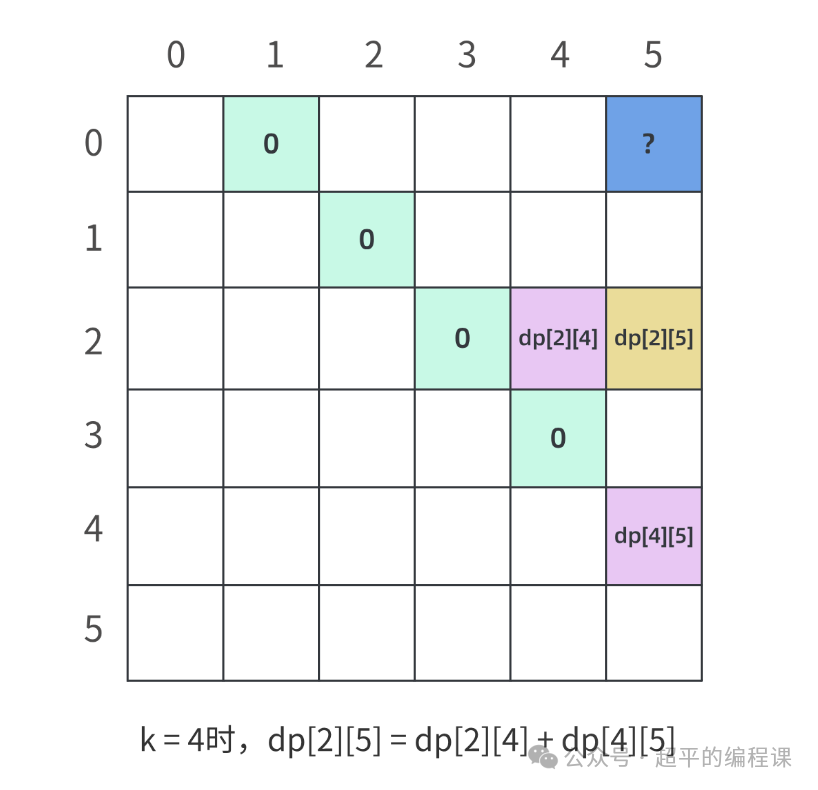
当k= 4时,计算如下:
dp[2][5] = dp[2][4] + dp[4][5] + p[2]* p[4] * p[5]对应的DP表格如图:
相信你已经发现了,在计算dp[2][5]的时候,它可以通过dp[2][3] + dp[3][5]计算出来,也可以通过dp[2][4] + dp[4][5]计算出来。
很显然,dp[2][3]、dp[3][5]、dp[2][4]、dp[4][5]这些单元格都在dp[2][5]的左方和下方,这就意味着不能使用传统的从上到下、从左到右。
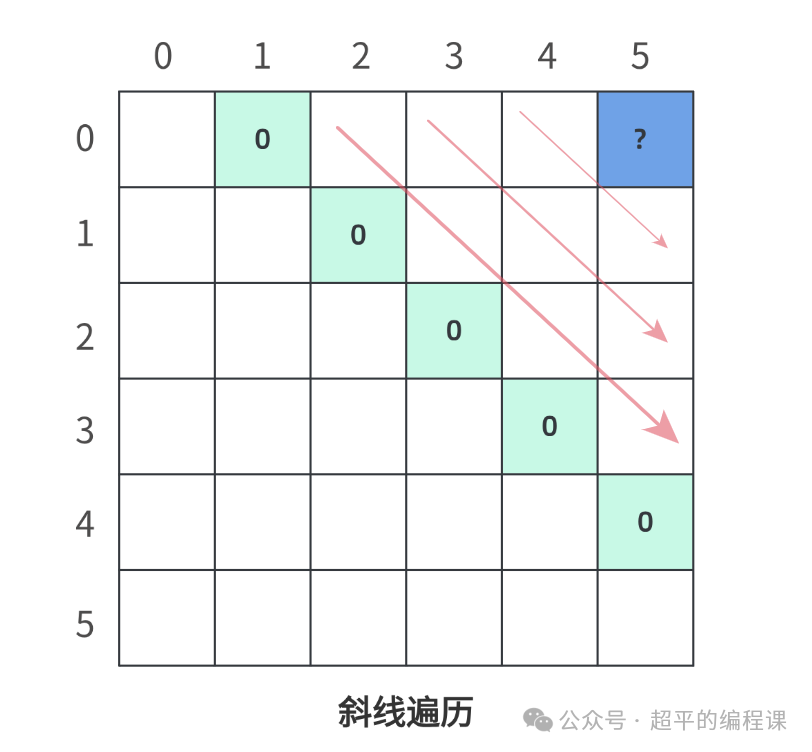
针对这种情况,我们可以有两种遍历方式,一是斜线遍历,如图:
二是从下到上,从左到右,如图:
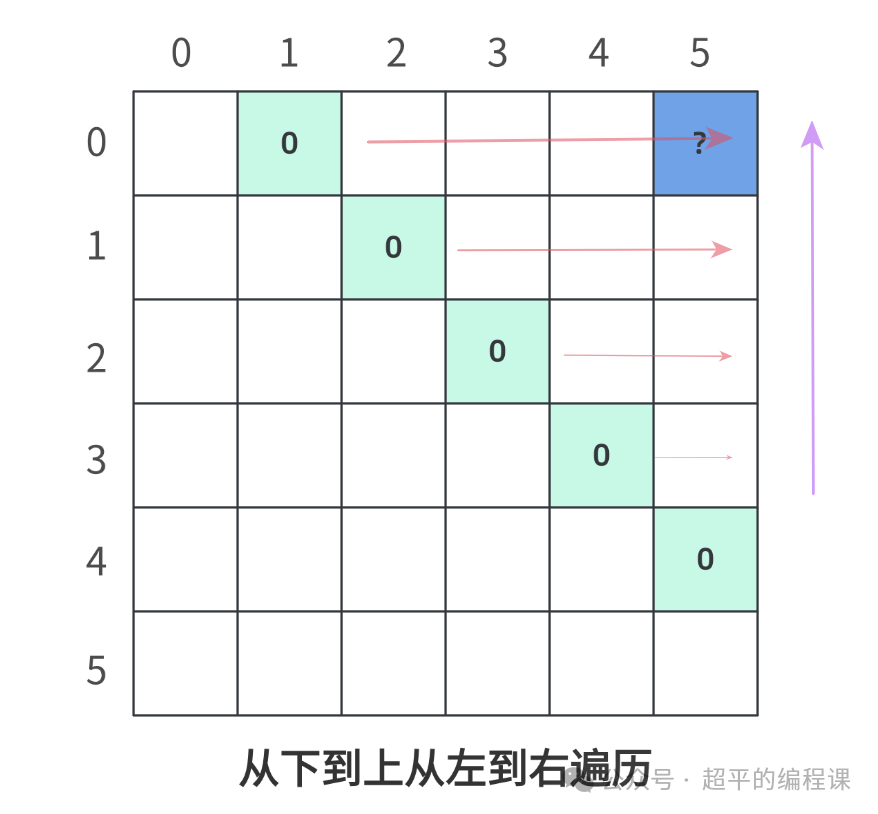
相对来说,使用第二种遍历方式更为简单一些。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们编写程序如下:
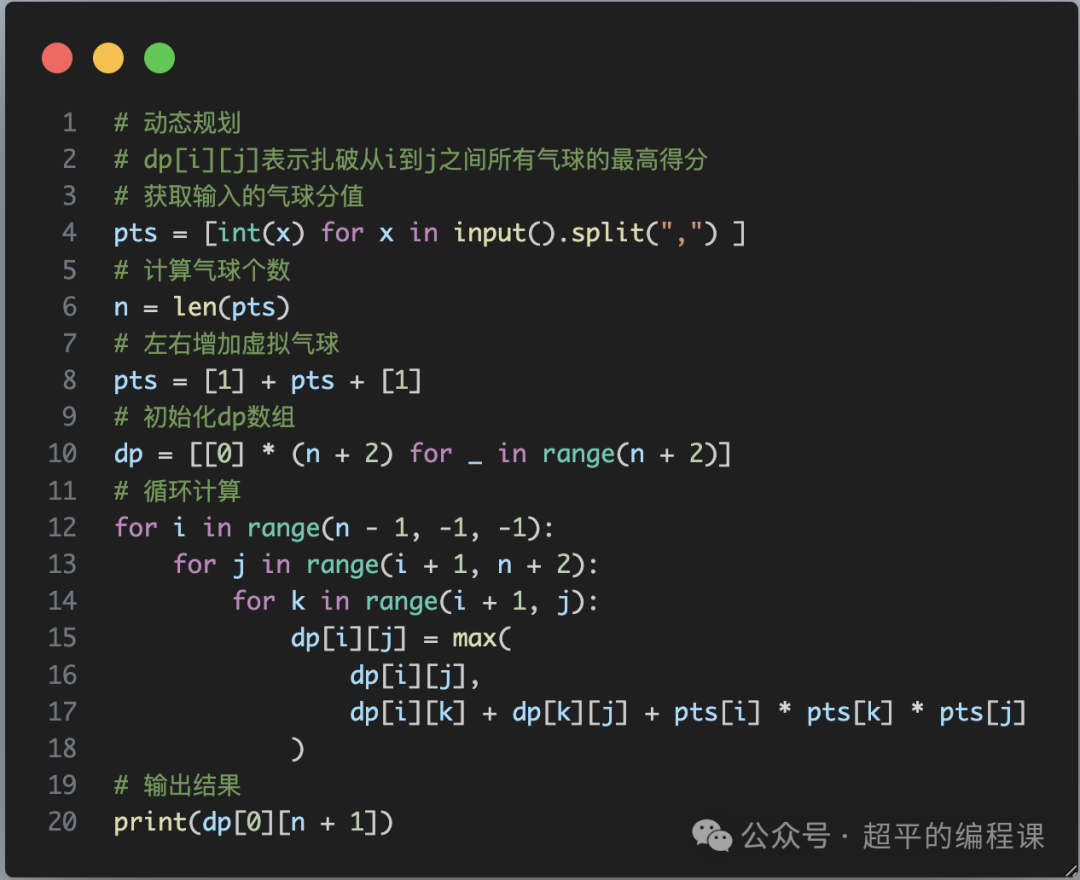
代码不多,说明4点:
1). pts表示输入的气球分值,左右各增加了一个分值为1的气球,这里直接使用列表相加的运算,非常方便;
2). 二维dp列表行和列都是n + 2,初始值为0,这里使用了列表推导式;
3). i表示行,从下到上,初始值是n -1,终点是0,j表示列,自左至右,初始值是i + 1,终点是n + 1;
4). k表示分割点,起始值是k+1,终点是j - 1。
至此,整个程序就全部完成了,你可以输入不同的数据来测试效果啦。
四.总结与思考
本题代码在10行左右,涉及到的知识点包括:
-
循环语句,尤其是嵌套循环;
-
列表的操作;
-
动态规划算法;
作为本次测评的最后一题,代码虽然不多,但是难度较大。关键点有两个,一是理解区间DP的算法思想,二是彻底弄清填充DP表格的方法和过程。
估计你已经发现了,最终的代码并不多,难的是过程分析,动态规划说难也难,说简单也简单。
动态规划说白了,就是根据题目意思定义一个表格,可能是一维的,也可能是二维的,然后找到规律,也就是状态转移方程,不断地计算并填充每一个单元格。
因此,在学习动态规划算法的时候,一定要亲自动手绘制并填充表格,这个过程会有些繁琐,但是效果非常好,写代码反倒是最简单的事情了。
超平老师给你留两道思考题:
1). 如何使用递归算法,计算最大分值?
2). 如果使用斜线遍历的顺序,代码又该怎么写呢?
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
这篇关于扎气球最高分-第13届蓝桥杯选拔赛Python真题精选的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





