本文主要是介绍完全背包+背包装满 总结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.背包恰好装满
(1)问题是什么
(2)问题的有效状态和无效状态
(3)问题的常考形式,以及如何去处理
1.值的大小
2.组合个数
3.排列个数
2.例题
A. Cut Ribbon
HDU1114 Piggy-Bank
1.背包恰好装满
(1)问题是什么
背包恰好装满的最大价值可以拆分成两个子问题
1.背包能否背恰好装满
2.如果可以恰好装满,那么恰好装满的时候的最大价值为多少
(2)问题的有效状态和无效状态
对于这种问题,背包的有效状态指的是背包为空,或者是背包恰好装满
无效状态指的是背包装了东西,但是没有装满
!!!!!!!!结论:任何有效状态都是由有效状态推出来的,无效状态无法推出有效状态
(3)问题的常考形式,以及如何去处理
1.值的大小
2.组合个数
3.排列个数
首先我们在这篇博客主要讨论的是值的大小,一般会有两种考向:
一个是容量为j的背包,最多能装多少物品
一个是容量为j的背包,最少能装多少物品
(1)对于第一个来说
既然其有效状态是为了求最大值,我们就要将无效状态的值变为一个最小值,这样完全背包的代码,无效值就无法去影响有效值的计算了
(2)对于第二个来说
和第一个相反,将无效状态变为一个最大值,别的没有任何区别
2.例题
A. Cut Ribbon
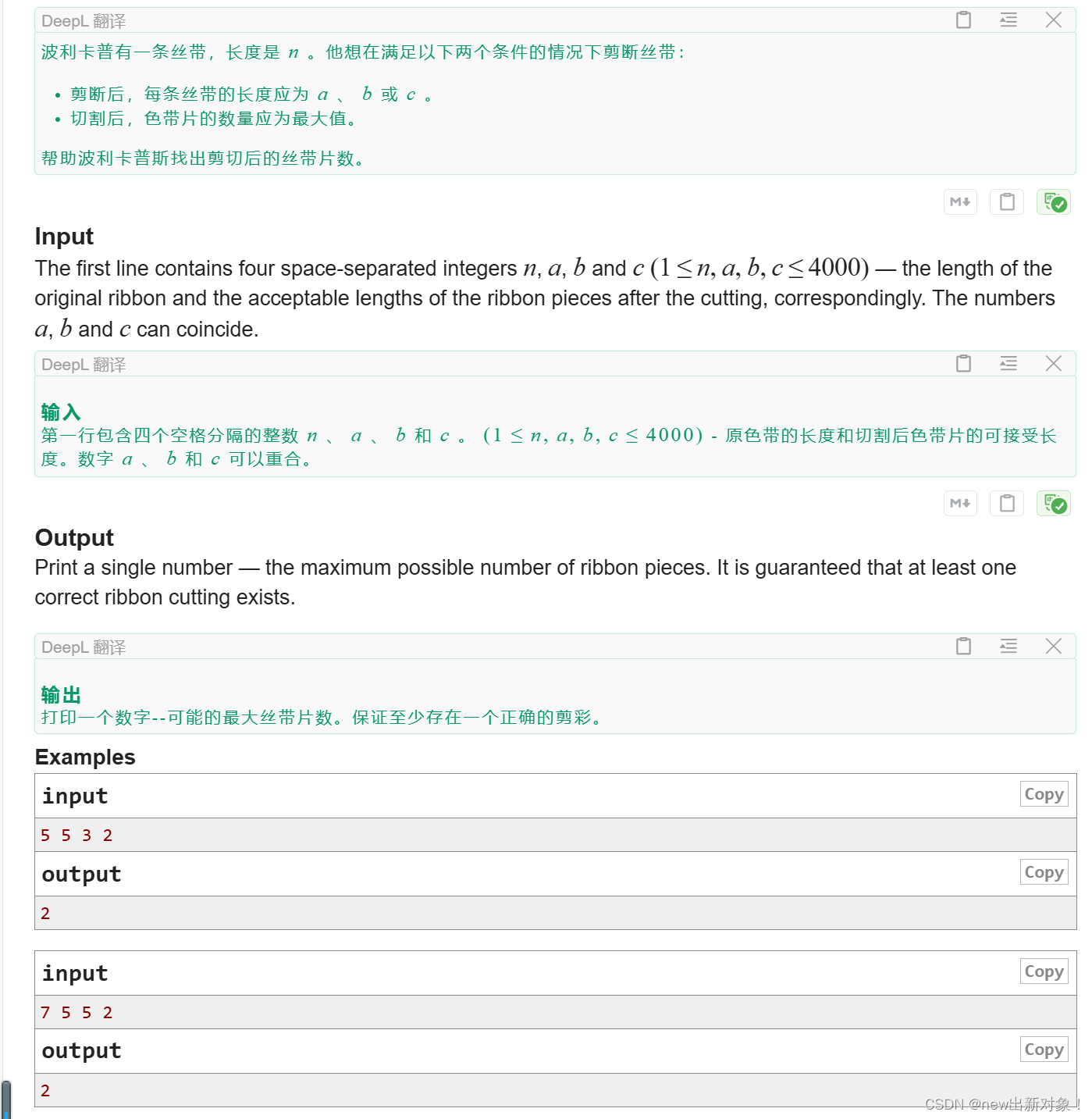
CF上一个div2的A题,那么必然就是一个简单的模版题了, 就是完全背包+判断背包装满是的最大的丝带数,然后就要用到我们的第一种情况了,让无效状态的值是一个int类型的最小值,然后正常去进行完全背包就可以直接拿下了
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n;
int a[5];
int dp[4005];signed main()
{cin>>n;for(int i=1;i<=3;i++){cin>>a[i];}memset(dp,-0x3f3f3f3f,sizeof(dp));//既然他想求最大值,那么我们就将非法状态设置为int类型的负无穷dp[0]=0;//长度为0,那肯定最大缎带数量为0;for(int i=1;i<=3;i++){for(int j=a[i];j<=n;j++){dp[j]=max(dp[j],dp[j-a[i]]+1);}}printf("%lld",dp[n]);return 0;
}HDU1114 Piggy-Bank

这个就相当于一个给我一个容量为f-e的背包,去判断这么个背包装满的时候,最少能装多少价值的物品,第二种情况,将无效状态设为int类型的最大值即可(我这边设置的是long long 类型的最大值,反正都是一个效果)
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
#define int long long
int t;
int e,f;
int n;
int w[505];
int p[505];
int dp[10005];//表示的是j公斤,所得到的最小价值为dp[j]
//因为要求最小金额,那么我们一上来给dp初始化为int最大值
signed main()
{cin>>t;while(t--){cin>>e>>f;cin>>n;for(int i=1;i<=n;i++){cin>>p[i]>>w[i];}memset(dp,0x3f3f3f3f3f3f3f3f,sizeof(dp));dp[0]=0;for(int i=1;i<=n;i++){for(int j=w[i];j<=f-e;j++){dp[j]=min(dp[j],dp[j-w[i]]+p[i]);}}if(dp[f-e]!=0x3f3f3f3f3f3f3f3f){printf("The minimum amount of money in the piggy-bank is %lld.\n",dp[f-e]);}if(dp[f-e]==0x3f3f3f3f3f3f3f3f)printf("This is impossible.");}return 0;
}这篇关于完全背包+背包装满 总结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








