白鹭群优化算法，原理详解，MATLAB代码免费获取

白鹭群优化算法（Egret Swarm Optimization Algorithm，ESOA）是一种受自然启发的群智能优化算法。该算法从白鹭和白鹭的捕食行为出发，由三个主要部分组成:坐等策略、主动策略和判别条件。将ESOA算法与粒子群算法(PSO)、遗传算法(GA)、差分进化算法(DE)、等算法在36个基准函数和3个工程问题上的性能进行了比较。结果证明了该方法的有效性和鲁棒性。

该成果于2022年发表在计算机领域三区期刊Biomimetics上，目前在谷歌学术上被引率39次。

大多数白鹭栖息在沿海岛屿、海岸、河口和河流，以及靠近海岸的湖泊、池塘、溪流、稻田和沼泽。白鹭通常是成对的，或者是成群的。由于飞行时能量消耗很大，决定捕食通常需要彻底检查飞行轨迹，以确保通过食物的位置获得的能量比飞行中消耗的能量要多。总体而言，采用积极搜索策略的大白鹭会平衡高能量消耗以获得更大的潜在回报，而采用坐等策略的雪白鹭则会平衡低能量消耗以获得更小但更可靠的利润。

1、算法原理

（1）数学模型与算法

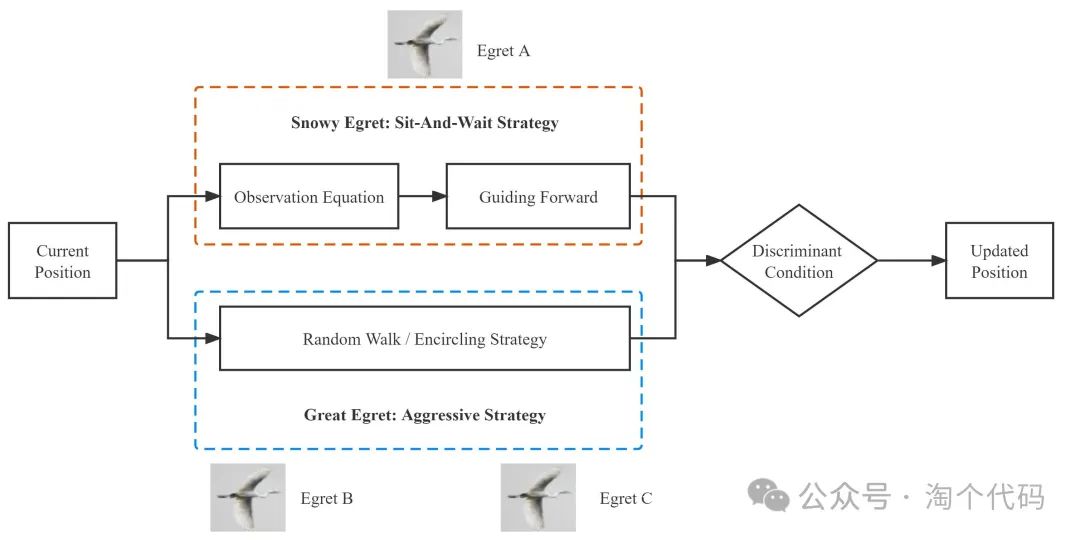
ESOA受白鹭的守株待兔策略和大白鹭的攻击策略的启发，结合了这两种策略的优点，构建了相应的数学模型来量化行为。如图所示，ESOA是一个并行算法，有三个基本组成部分：坐等策略，积极策略和判别条件。一个白鹭小队中有三只白鹭，白鹭A采用引导前进机制，白鹭B和白鹭C分别采用随机行走和包围机制。每一部分的细节如下。

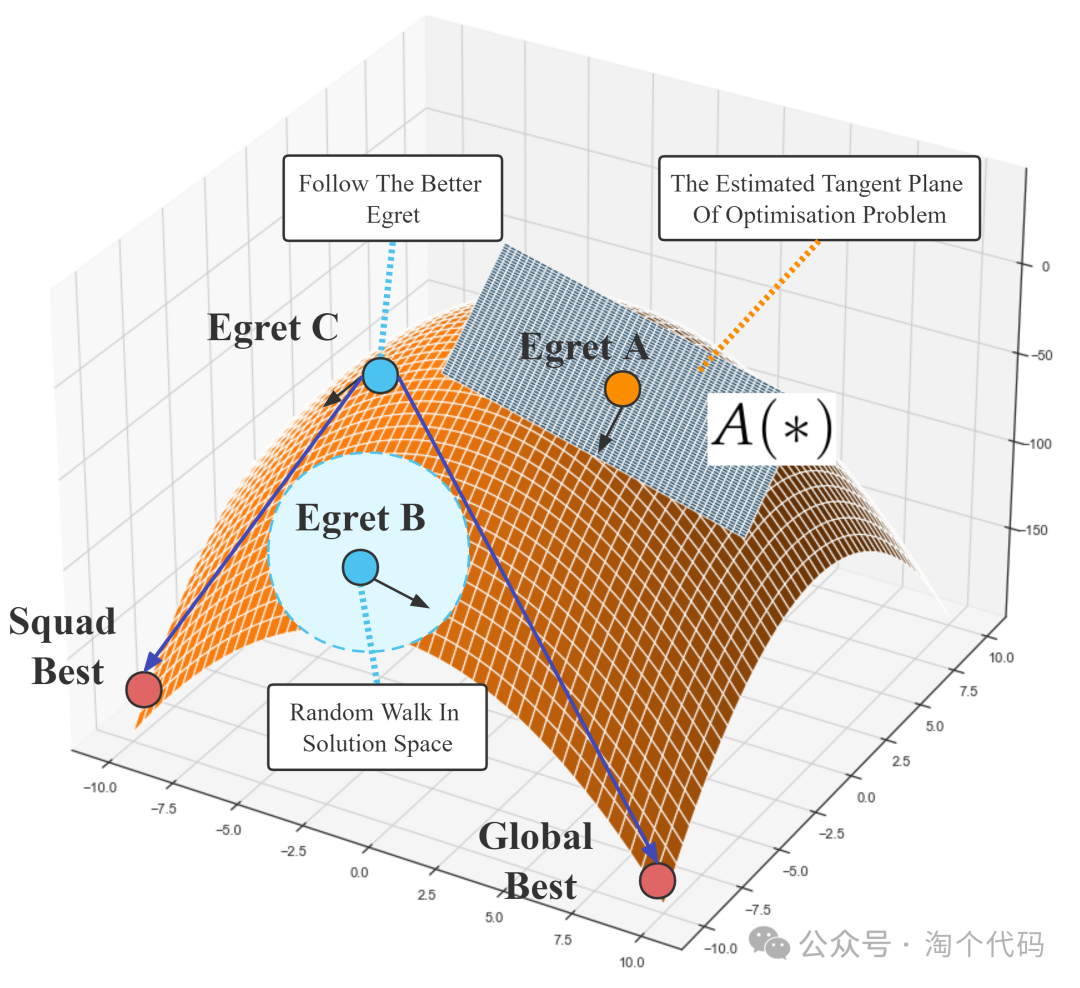
Egret Squad的各个角色和搜索首选项如图所示。白鹭A将估计下降平面并基于平面参数的梯度进行搜索，白鹭B执行全局随机漫游，白鹭C基于更好的白鹭的位置选择性地进行探索。通过这种方式，ESOA在开发和勘探方面将更加平衡，并能够快速搜索可行的解决方案。与梯度下降不同，ESOA在梯度估计中引用了历史信息和随机性，这意味着它不太可能落入优化问题的鞍点。ESOA也不同于其他的元启发式算法，通过估计优化问题的切平面，使快速下降到当前的最优点。

（2）坐等策略

观测方程：假设第i个白鹭小队的位置为Xi ∈ Rn，n为问题的维数，A（n）为白鹭对当前位置可能存在的猎物的估计方法。是对当前位置猎物的估计，

则估计方法可以被参数化为，

其中wi ∈ Rn是估计方法的权重。误差ei可以描述为，

同时，ω i的实际梯度ω gi ∈ Rn可以通过对误差方程（3）的wi进行偏导数来恢复，其方向为d ω i。

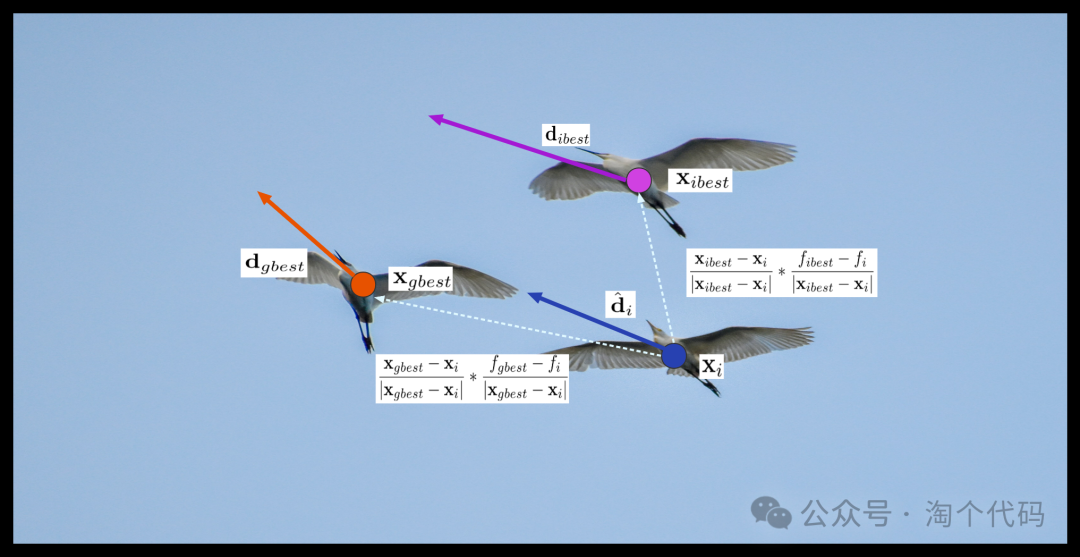
下图展示了白鹭的跟随行为，其中白鹭在捕食过程中参考了更好的白鹭，借鉴了它们估计猎物行为的经验并融入了自己的想法。dh，i ∈ Rn是小队最佳位置的方向修正，而dg，i ∈ Rn是所有小队最佳位置的方向修正。

积分梯度gi ∈ Rn可以表示如下，并且rh ∈ [0，0.5），rg ∈ [0，0.5）：

这里应用自适应权重更新方法[76]，β1为0.9，β2为0.99：

根据白鹭A对当前情况的判断，下一个采样位置xa，i可以描述为，

其中t和tmax是当前迭代时间和最大迭代时间，而hop是解空间的下界和上界之间的差距。stepa ∈（0，1]是白鹭A的步长因子。ya，i是xa，i的适合度。

（3）积极的战略

白鹭B倾向于随机搜索猎物，其行为可描述如下，

其中rb，i是（− π/2，π/2）中的随机数，xb，i是白鹭B的预期下一个位置，yb，i是适应度。

白鹭C喜欢攻击性地追逐猎物，因此使用包围机制作为其位置的更新方法：

（4）判别条件

在白鹭小队的每个成员都决定了自己的计划后，小队会选择最佳方案并一起采取行动。xs，i是第i个白鹭小队的解矩阵：

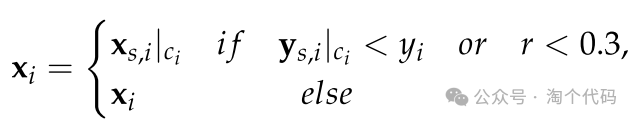
如果最小值ys,i优于当前适应度yi，则白鹭队接受该选择。或者随机数r∈(0,1)小于0.3，这意味着有30%的可能性接受更差的方案。

ESOA对应的算法的伪代码如下所示。

2、结果展示

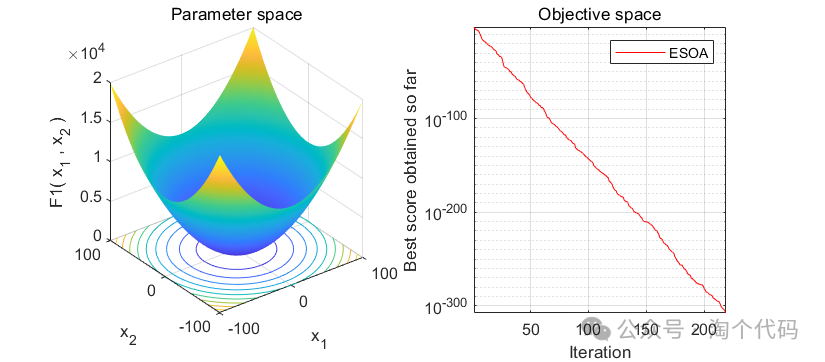
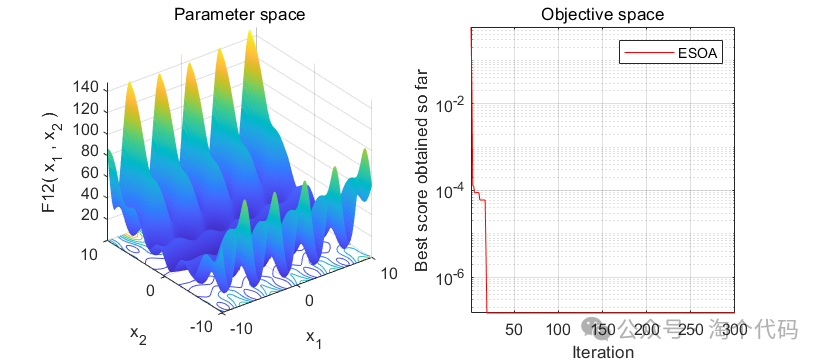
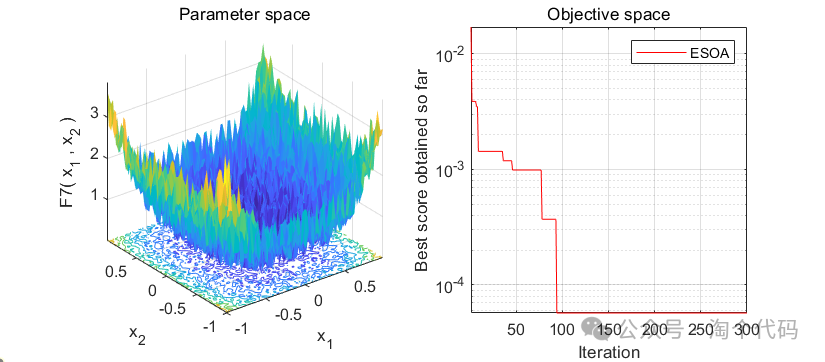
3、MATLAB核心代码

%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [y_global_best, x_global_best, Convergence_curve]=ESOA(SearchAgents_no, Max_iter, lb, ub, dim, fobj)
func = fobj;
beta1 = 0.9;
beta2 = 0.99;
x=initialization(SearchAgents_no, dim, ub, lb);
Convergence_curve=zeros(1,Max_iter);
w = random('Uniform', -1, 1, SearchAgents_no, dim);
%g = random('Uniform', -1, 1, SearchAgents_no, dim);
m = zeros(SearchAgents_no, dim);
v = zeros(SearchAgents_no, dim);
y = zeros(SearchAgents_no,1);
for i=1:SearchAgents_noy(i) = func(x(i,:));
end
p_y = y;
x_hist_best = x;
g_hist_best = x;
y_hist_best = ones(SearchAgents_no)*inf;
x_global_best = x(1, :);
g_global_best = zeros(1, dim);
y_global_best = func(x_global_best);
hop = ub - lb;
l=0;% Loop counter
% Main loop
while l<Max_iterfor i=1:SearchAgents_nop_y(i) = sum(w(i, :) .* x(i, :));p = p_y(i) - y(i);g_temp = p.*x(i, :);% Indivual Directionp_d = x_hist_best(i, :) - x(i, :);f_p_bias = y_hist_best(i) - y(i);p_d = p_d .* f_p_bias;p_d = p_d ./ ((sum(p_d)+eps).*(sum(p_d)+eps));d_p = p_d + g_hist_best(i, :);% Group Directionc_d = x_global_best - x(i, :);f_c_bias = y_global_best - y(i);c_d = c_d .* f_c_bias;c_d = c_d ./ ((sum(c_d)+eps).*(sum(c_d)+eps));d_g = c_d + g_global_best;% Gradient Estimationr1 = rand(1, dim);r2 = rand(1, dim);g = (1 - r1 - r2).*g_temp + r1 .* d_p + r2 .* d_g;g = g ./ (sum(g) + eps);m(i,:) = beta1.*m(i,:)+(1-beta1).*g;v(i,:) = beta2*v(i,:)+(1-beta2)*g.^2;w(i,:) = w(i,:) - m(i,:)/(sqrt(v(i,:))+eps);% Advice Forwardx_o = x(i, :) + exp(-l/(0.1*Max_iter)) * 0.1 .* hop .* g;Flag4ub=x_o>ub;Flag4lb=x_o<lb;x_o = (x_o.*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;y_o = func(x_o);% Random Searchr = random('Uniform', -pi/2, pi/2, 1, dim);x_n = x(i, :) + tan(r) .* hop/(1 + l) * 0.5;Flag4ub=x_n>ub;Flag4lb=x_n<lb;x_n = (x_n.*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;y_n = func(x_n);% Encircling Mechanismd = x_hist_best(i, :) - x(i, :);d_g = x_global_best - x(i, :);r1 = rand(1, dim);r2 = rand(1, dim);x_m = (1-r1-r2).*x(i, :) + r1.*d + r2.*d_g;Flag4ub=x_m>ub;Flag4lb=x_m<lb;x_m = (x_m.*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;y_m = func(x_m);% Discriminant Conditionx_summary = [x_m; x_n; x_o];y_summary = [y_m, y_n, y_o];y_summary(isnan(y_summary)) = inf;ind = y_summary==min(y_summary);y_i = min(y_summary);x_i = x_summary(ind, :);x_i = x_i(1, :);if y_i < y(i)y(i) = y_i;x(i, :) = x_i;if y_i < y_hist_best(i)y_hist_best(i) = y_i;x_hist_best(i, :) = x_i;g_hist_best(i, :) = g_temp;if y_i < y_global_besty_global_best = y_i;x_global_best = x_i;g_global_best = g_temp;endendelseif rand()<0.3y(i) = y_i;x(i, :) = x_i;endendend    
l=l+1;    
fprintf("%d, %f\n", l, y_global_best)
Convergence_curve(l) = y_global_best;
end
end

参考文献

[1]Chen Z, Francis A, Li S, et al. Egret swarm optimization algorithm: an evolutionary computation approach for model free optimization[J]. Biomimetics, 2022, 7(4): 144.

完整代码获取

后台回复关键词：

TGDM833