本文主要是介绍动规解决01背包/完全背包精讲,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

还不会用动态规划解决01背包/完全背包?看这一篇文章就够了!
首先我们要明白什么是01背包和完全背包。
背包问题总体问法就是:
你有一个背包,最多能容纳的体积是V。
现在有n个物品,第i个物品的体积为vi ,价值为wi。
现在有n种物品,每种物品有任意多个,第i种物品的体积为vi ,价值为wi。
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
根据物品个数是唯一还是无限多个,如果只能装一个,就是01背包问题;如果同一个物品能装无限多个,就是完全背包问题。
问法的区别:
同样也是分为两类,第一种就是必须将背包恰好装满,第二种问法是背包不必装满。
在弄清楚什么是01背包和完全背包后,我们来正式学习如何解决这类问题吧!
我们首先来详细讲解01背包和完全背包的母题(模板),然后会有相应的例题,同样也有详解给到大家!
一、01背包
【模板】01背包_牛客题霸_牛客网 (nowcoder.com)

我们先解决第一问,背包没有必须装满的情况下。
用动态规划解决问题有下面的标准步骤:
1、状态表示:
dp[i][j] 表示从前i个物品中挑选,总体积不超过j,所有选法中能挑选出的最大价值。
有同学会问,状态表示为什么是这样的呢?因为这样我们会包含物品个数和体积,也没必要多想,可以直接记住!
2、状态转移方程
根据最后一步的状况,分情况讨论。
这里的dp[i][j]分为两种情况:
- 不选i物品:dp[i-1][j]:此时状态表示就是第i-1个物品状态,直接照抄即可
- 选i物品:dp[i-1][j-v[i]]+w[i]:因为我们已经挑选了第i个物品,因此第i个物品的价值一定是先加上的。在我们选了第i个物品的情况下,我们就需要找在前i-1个物品中体积等于j-v[i]的状态。当然这里的前提是必须 j-v[i] 要大于等于0,从坐标要大于等于0 也可以看出!
综上,状态转移方程就是求这两者的最大值。
3、初始化
根据经验,我们必须多一层空间,防止下标越界。
根据转移方程,我们我们发现对于列是不会产生越界的,因为我们对于列下标都会有j-v[i] >= 0判断!
所以我们只需要考虑行初始化,下面的背包问题也是如此,列的下标越界问题不用考虑!只需要考虑行的初始化。
在第0行,表示在前0个物品中,总体积为j所表示的总价值,不存在,所以可以直接初始化为0。
4、填表顺序
根据状态转移方程可知,由上到下,由左到右。
5、返回值
由题意中的求这个背包至多能装多大价值的物品,所以我们返回dp[n][V].
n表示一共有n个物品,V表示背包所能容纳的最大体积。
我们继续解决第二问,背包必须装满的情况下。
1、状态表示
dp[i][j] 此时状态表示要与第一问进行区分:
dp[i][j] 表示从前i个物品中挑选,总体积正好等于j,所有选法中能挑选出的最大价值。
2、状态转移方程
大部分内容与第一问相同,但是我们要考虑在前i个物品中挑选,可能体积要求不满足,也就是条件不存在的情况!
因此我们需要将不成立的部分要特殊处理!!!目的都是为了不要使用这些不存在的值
第一种,将不存在的情况赋值成-1.
第二种,将这些值赋值成0x3f3f3f3f,表示最大值,或者负的,表示最小值。

3、初始化
还是跟之前一样,第一列不需要初始化。
第一行的第一个数存在,赋值为0。但是后面的值就不存在,在前0个物品中,挑选出体积正好为1、2、3……这些情况都不存在,所以赋值为-1
4、填表顺序
从上往下
5、返回值
dp[n][V]
空间优化:
1、利用滚动数组在空间上的优化
我们可以直接用一维dp数组去代替二维数组

2、直接在原始的代码上稍加修改即可

直接将横坐标删除,然后遍历顺序修改成从右往左。
为何遍历顺序改成从右往左?因为我们在初始化dp表时,用到了左上角的值,而一维滚动初始化时从左往右会导致新一轮的值会被覆盖、修改掉。因此需要从右往左进行初始化dp表!
空间优化后的代码
#include <iostream>
#include<bits/stdc++.h>
using namespace std;int dp[1010];
int v[1010];
int w[1010];int main()
{int n = 0, V = 0;cin >> n >> V;for(int i = 1; i <= n; i++){cin >> v[i] >> w[i];}//解决第一问for(int i = 1; i <= n; i++){for(int j = V; j >= v[i]; j--){dp[j] = max(dp[j], w[i]+dp[j-v[i]]);}}cout << dp[V] << endl;//解决第二问memset(dp,0,sizeof(dp));for(int i = 1; i <= V; i++) dp[i] = -1;for(int i = 1; i <= n; i++){for(int j = V; j >= 1; j--){if(j >= v[i] && dp[j-v[i]] != -1){dp[j] = max(dp[j], w[i]+dp[j-v[i]]);}}}if(dp[V] == -1) cout << 0;else cout << dp[V];return 0;
}
二、完全背包
【模板】完全背包_牛客题霸_牛客网 (nowcoder.com)

我们先解决第一问,背包没有装满的情况下。
1、状态表示:
跟01背包状态表示一致。
dp[i][j] 表示从前i个物品中挑选,总体积不超过j,所有选法中能挑选出的最大价值。
2、状态转移方程
01背包和完全背包的本质区别就是能选择数量不一样,01背包数量只有1个,而完全背包可选择物品数量有无限多个。
因此状态转移方程根据可选择物品数量分为很多种。

那有无限多种,如何将其转化为只有一种状态或者两种状态呢?
根据数学知识将纵坐标j 进行代换变成 j-v[i],进行如下证明即可得:

最终的方程就是:
dp[j] = max(dp[j], dp[j-v[i]] + w[i]);
这里可以直接记忆最后的答案,证明过程了解。
简记就是将第一个状态转移表达式中的横坐标加1即可!
3、初始化
只需要初始化第一行初始化为0即可
4、填表顺序
根据状态转移方程,从上往下填写每一行,每一行从左往右
5、返回值
dp[n][V]
我们继续解决第二问,背包必须装满的情况下。
1、状态表示
dp[i][j] 此时状态表示要与第一问进行区分:
dp[i][j] 表示从前i个物品中挑选,总体积正好等于j,所有选法中能挑选出的最大价值。
2、状态转移方程
与第一问的区别就是:需要用-1额外表示不存在的状态。

3、初始化
将不存在的情况赋值为-1。
第一行除了第一个位置其余都不存在。

4、填表顺序
同第一问
5、返回值
同第一问
空间优化:
同样也是利用滚动数组进行空间优化。
注意这里与01背包的区别就是从左往右遍历。
区分:
01背包从右往左遍历的原因是他运用到了上一行的值,因为是横坐标是 i-1
而完全背包的状态转移方程的横坐标是i
这两者状态转移方程的区别也决定了他们在初始化方向的问题!!!
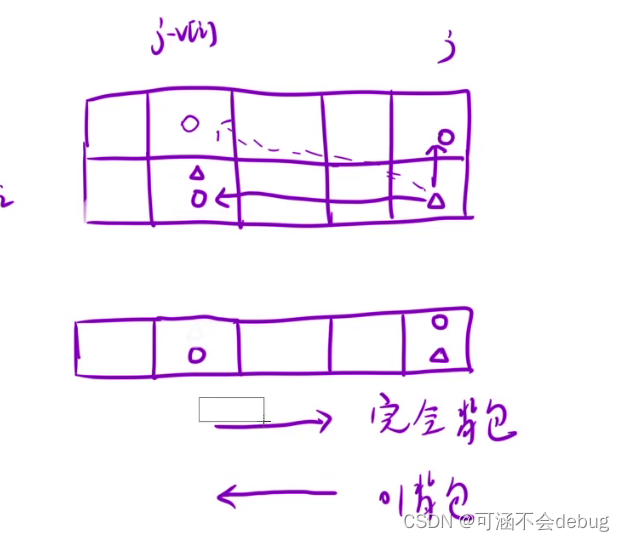
虚线表示01背包的方向,实现表示完全背包的方向。
最终优化后的代码:
#include <iostream>
#include<bits/stdc++.h>
using namespace std;int v[1010];
int w[1010];int dp[1010];int main()
{ int n = 0, V = 0;cin >> n >> V;for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];//vector<vector<int>> dp(n+1, vector<int>(V+1));//解决第一问for(int i = 1; i <= n ; i++){//从左往右遍历for(int j = 1; j <= V ; j++){if(j-v[i] >= 0){dp[j] = max(dp[j], dp[j-v[i]] + w[i]);}}}cout << dp[V] << endl;//解决第二问memset(dp,0,sizeof(dp));//先初始化为-1for(int i = 1; i <= V; i++) dp[i] = -1;for(int i = 1; i <= n ; i++){for(int j = 1; j <= V ; j++){if(j-v[i] >= 0 && dp[j-v[i]] != -1){dp[j] = max(dp[j], dp[j-v[i]] + w[i]);}}}if(dp[V] == -1) cout << 0;else cout << dp[V];return 0;
}这篇关于动规解决01背包/完全背包精讲的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







