本文主要是介绍栈与队列OJ题【括号适配问题】【用队列实现栈】【用栈实现队列】【设计循环队列】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一.有效的括号
OJ链接

这一道题我们就可以用栈来解决:
不了解栈的可以看我的上一篇博客。
typedef char STDataType;
//用数组来实现栈
typedef struct stack
{STDataType* a;int capacity;int top;
}ST;
void STInit(ST* pst)
{assert(pst);pst->a = NULL;pst->capacity = 0;//在后面往栈里面放元素的时候,最后的top是在栈顶的下一个位置pst->top = 0;//如果是-1,那么代表的就是下标//pst->top = -1;
}
void STDestory(ST* pst)
{free(pst->a);pst->a = NULL;pst->capacity = pst->top = 0;
}
//入栈
void STPush(ST* pst, STDataType x)
{assert(pst);if (pst->top == pst->capacity)//如果top的数值刚好等于栈的总容量,那么栈就是满了,包含为0的情况。{int newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;STDataType* tmp = (STDataType*)realloc(pst->a, sizeof(STDataType) * newcapacity);//用realloc改变我们申请动态存储空间的大小if (tmp == NULL){perror("STPush::relloc");return;}pst->a = tmp;//成功改变了空间,就赋值给栈里的a。pst->capacity = newcapacity;//总体的容量也随之变化。}pst->a[pst->top] = x;pst->top++;//因为我们的top的栈顶的位置,所以在每一次赋值完毕后就递增。
}//出栈
void STPop(ST* pst)
{assert(pst);assert(pst->top > 0);pst->top--;
}//读取栈顶元素
STDataType STTop(ST* pst)
{assert(pst);assert(pst->top > 0);return pst->a[pst->top-1];
}//判空
bool STEmpty(ST* pst)
{assert(pst);return pst->top == 0;
}
//获取数据个数
int STSize(ST* pst)
{assert(pst);return pst->top;
}
bool isValid(char* s)
{ST p;STInit(&p);//初始化栈int sz=strlen(s);//求出栈里的总元素for(int i=0;i<sz;i++){if(s[i]=='('||s[i]=='['||s[i]=='{'){STPush(&p,s[i]);//如果与三种左括号匹配上了,就入栈}else//否则就是右括号的情况{if(STEmpty(&p))//这里有一个判空,目的就是我们的栈里必须要有左括号,不然我们已经进入else了,这里就只有可能是右括号,而这个右括号就不可能与左括号匹配上了{STDestory(&p);//如果进入了这个if语句,就说明不可能匹配上了return false;}char top=STTop(&p);//取出都是左括号栈里的头栈元素STPop(&p);if((top=='('&&s[i]!=')')||(top=='['&&s[i]!=']')||(top=='{'&&s[i]!='}')){STDestory(&p);//这个if语句就是,虽然栈里有左括号,同时也匹配到了右括号,但是括号直接不匹配的问题return false;}}}bool ret=STEmpty(&p);//如果栈为空了,就是说所以的括号都匹配上了STDestory(&p);return ret;
}这个题主要需要注意的地方就是我们入栈入的都是左括号,右括号就单独的一个一个的与栈里的左括号相匹配。总的来说不算难,就是让我们了解一下栈的应用。
二.用队列实现栈
OJ链接

简单的说呢,就是我们使用队列的先进先出的特点来完成栈的先进后出的特点。对于队列不熟悉的朋友,也可以看我们上一篇博客。
//先来完成队列的实现
typedef int QDataType;
typedef struct QNode//我们用链表来实现队列
{QDataType val;struct QNode* next;
}QNode;
typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;
//队列初始化
void QInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}
//队列的销毁
void QDestroy(Queue* pq)
{assert(pq);QNode* pcur = pq->phead;while (pcur)//遍历整个链表{QNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
//入队
void QPush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("newnode");return;}newnode->next = NULL;newnode->val = x;if (pq->size == 0)//链表没有节点{pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = pq->ptail->next;}pq->size++;//用size记录链表节点的个数,也就是队列里元素的个数
}
//出队列
void QPop(Queue* pq)
{assert(pq);assert(pq->phead);//出队列之前队列里一定要有元素if (pq->phead == pq->ptail)//一个节点{free(pq->phead);pq->phead = pq->ptail = NULL;}else//多个节点{QNode* pcur = pq->phead->next;free(pq->phead);pq->phead = pcur;}pq->size--;//出一个,减一个
}
//取队头元素
QDataType QTop(Queue* pq)
{assert(pq);assert(pq->phead);return pq->phead->val;
}
//取队尾元素
QDataType QBack(Queue* pq)
{assert(pq);assert(pq->ptail);return pq->ptail->val;
}
//求队列里元素个数
int QSize(Queue* pq)
{assert(pq);return pq->size;
}
//判空
bool QEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}//开始写题
typedef struct {Queue q1;Queue q2;
} MyStack;//创建两个队列//初始化栈
MyStack* myStackCreate()
{MyStack* pst = (MyStack*)malloc(sizeof(MyStack));QInit(&(pst->q1));QInit(&(pst->q2));//因为pst->q是队列,所以调用上面写的初始化队列的函数return pst;
}
//入栈
void myStackPush(MyStack* obj, int x) {if (!QEmpty(&(obj->q1)))//这里的入队列,我们入的队列是为空的那一个{QPush(&(obj->q1), x);}else{QPush(&(obj->q2), x);}
}
//出栈
int myStackPop(MyStack* obj)
{//假设法,创建两个新的队列,一个为空队列,一个不为空Queue* empty = &(obj->q1);Queue* noempty = &(obj->q2);if (!QEmpty(&(obj->q1))){empty = &(obj->q2);noempty = &(obj->q1);}//假设法完成后我们就只需要对empty和noempty进行改变while (QSize(noempty) > 1)//这里的循环和大于1的意思是,我们要把非空的队列入到为空的队列里,但是要剩余一个元素。{QPush(empty, QTop(noempty));QPop(noempty);}int top = QTop(noempty);//上面我们剩余的那个元素就是作为栈先进后出的那个元素(后面再单独解释一下)QPop(noempty);return top;
}
//提取栈顶元素
int myStackTop(MyStack* obj) {if (!QEmpty(&(obj->q1))){return QBack(&(obj->q1));//队尾实际上就是栈顶}else{return QBack(&(obj->q2));}
}
//判空
bool myStackEmpty(MyStack* obj) {return QEmpty(&(obj->q1)) && QEmpty(&(obj->q2));
}void myStackFree(MyStack* obj) {QDestroy(&(obj->q1));QDestroy(&(obj->q2));free(obj);
}
不能理解的可以看一下图:
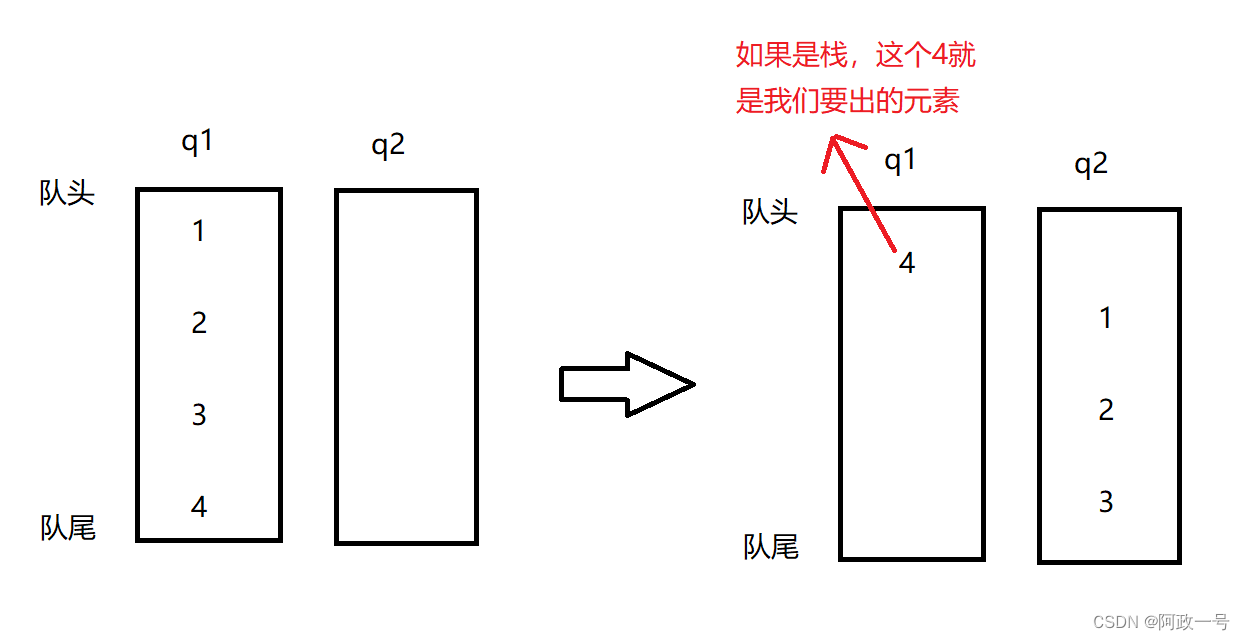
相对于队列来说,如果要实现先进后出的特点,就要不断的往空队列移动元素,且移动的时候一定要保留一个,这个保留的元素相对于栈来说,就是我们要出栈的第一个元素。
三.用栈实现队列
OJ链接
同样的,解决这道题,依然要先实现一下栈。
typedef int SLTDataType;
typedef struct Stack
{SLTDataType* a;int top;int capacity;
}ST;
void STInit(ST* pst)
{assert(pst);pst->a = NULL;pst->capacity = 0;//top的位置在栈顶的后面的一个位置pst->top = 0;
}
void STDestory(ST* pst)
{assert(pst);free(pst->a);pst->a = NULL;pst->capacity = pst->top = 0;
}
void STPush(ST* pst, SLTDataType x)
{assert(pst);if (pst->top == pst->capacity){int newcapacity = pst->capacity == 0 ? 4 : 2 * pst->capacity;SLTDataType* tmp = (SLTDataType*)realloc(pst->a, newcapacity * sizeof(SLTDataType));if (tmp == NULL){perror("STPush::realloc");return;}pst->a = tmp;pst->capacity = newcapacity;}pst->a[pst->top] = x;pst->top++;
}
void STPop(ST* pst)
{assert(pst);assert(pst->top > 0);pst->top--;
}
SLTDataType STTop(ST* pst)
{assert(pst);assert(pst->top > 0);return pst->a[pst->top - 1];
}
bool STEmpty(ST* pst)
{assert(pst);return pst->top == 0;
}//正式开始实现队列
typedef struct {ST pushst;ST popst;
} MyQueue;//初始化队列
MyQueue* myQueueCreate() {MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));STInit(&obj->pushst);STInit(&obj->popst);return obj;
}
//入队
void myQueuePush(MyQueue* obj, int x) {STPush(&obj->pushst,x);//把需要入队的元素全部放在pushst里
}
//出队+删除
int myQueuePop(MyQueue* obj) {int front=myQueuePeek(obj);//调用下面的Peek函数,取出要出队的元素STPop(&obj->popst);然后删除return front;
}
//出队
int myQueuePeek(MyQueue* obj) {if(STEmpty(&obj->popst))//判断要popst是否为空{while(!STEmpty(&obj->pushst))//popst为空了并且pushst里面有元素{int top=STTop(&obj->pushst);//提取pushst里的元素STPush(&obj->popst,top);//放到popst里面STPop(&obj->pushst);//删除刚刚出去的pushst里的栈顶元素}}//这里的if语句和while语句的作用就是把pushst里的元素反过来放入到popst里面return STTop(&obj->popst);//最后在返回出栈的值,这个值就是我们要的先进先出的值
}
//判空
bool myQueueEmpty(MyQueue* obj) {return STEmpty(&obj->pushst)&&STEmpty(&obj->popst);
}
//释放
void myQueueFree(MyQueue* obj) {STDestory(&obj->pushst);STDestory(&obj->popst);free(obj);
}这道题的思路就是先创建两个栈,一个专门用来入,一个专门用来出。要出栈的话就用popst。
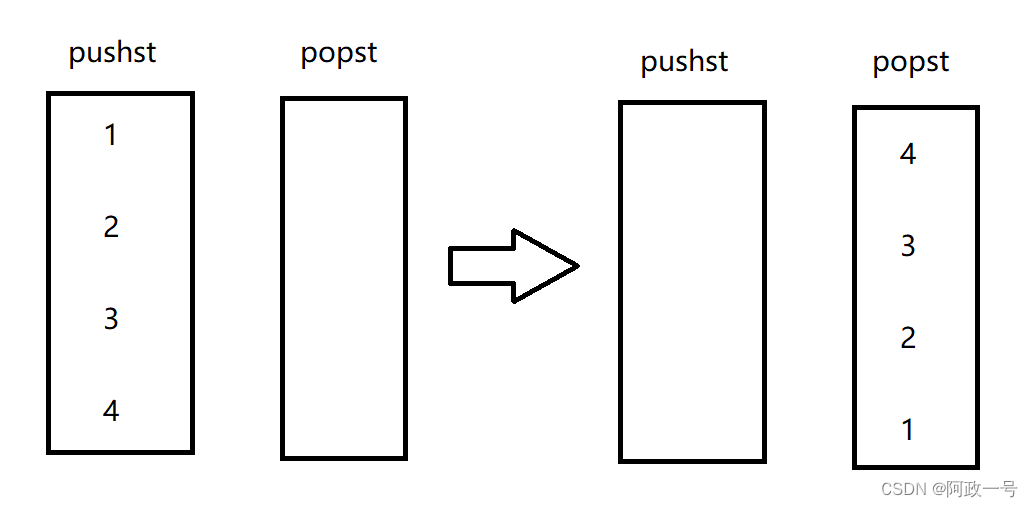
等到我们把所有的元素都移动到popst里面的时候,再用栈的性质出栈,此时出来的元素的顺序将会是1,2,3,4。符合我们需要的特性,大家也可以试试入栈什么的。
四.设计循环队列
OJ链接
typedef struct {int* a;int head;int tail;//指向尾的下一个int k;//k是队列里所有的元素个数的总数
} MyCircularQueue;MyCircularQueue* myCircularQueueCreate(int k) {MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));obj->a = (int*)malloc(sizeof(int) * (k + 1));//多创建一个sizeof(int)obj->head = 0;obj->tail = 0;obj->k = k;return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {return obj->tail == obj->head;//如果head==tail就说明没有元素
}bool myCircularQueueIsFull(MyCircularQueue* obj) {return (obj->tail + 1) % (obj->k + 1) == obj->head;//这里取了一个模,是为了避免tail在k位置时的情况
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {if (myCircularQueueIsFull(obj))//满了就不能入了return false;obj->a[obj->tail] = value;//tail指向的是队尾的下一个位置obj->tail++;//可以分为正常情况和tail在k位置上的情况obj->tail %= (obj->k + 1);//有这个主要是为了避免tail在K位置上的情况return true;
}bool myCircularQueueDeQueue(MyCircularQueue* obj) {if (myCircularQueueIsEmpty(obj))return false;obj->head++;//删除队头的元素,直接head++就行了obj->head %= (obj->k + 1);//跟tail在k位置是同一个道理return true;
}int myCircularQueueFront(MyCircularQueue* obj) {if (myCircularQueueIsEmpty(obj))return -1;return obj->a[obj->head];//直接返回队头元素
}int myCircularQueueRear(MyCircularQueue* obj) {if (myCircularQueueIsEmpty(obj))return -1;elsereturn obj->a[(obj->tail + obj->k) % (obj->k + 1)];//因为tail指向的是队尾的下一个位置,所以要小心一下tail在k位置的情况
}void myCircularQueueFree(MyCircularQueue* obj) {free(obj->a);free(obj);
}这里需要单独解释一下一个东西:
int myCircularQueueRear(MyCircularQueue* obj) {if (myCircularQueueIsEmpty(obj))return -1;elsereturn obj->a[(obj->tail + obj->k) % (obj->k + 1)];//因为tail指向的是队尾的下一个位置,所以要小心一下tail在k位置的情况
}注意我return的是什么:(obj->tail + obj->k) % (obj->k + 1)这个东西又可以写成(obj->tail-1 + obj->k+1) % (obj->k + 1)。obj->tail-1加上一个obj->k + 1再取obj->k + 1的余。最后的结果不会有改变,但是多加了这一步就完美的避免了,tail在0位置的情况。如果直接return的是tail-1会存在访问越界的问题。
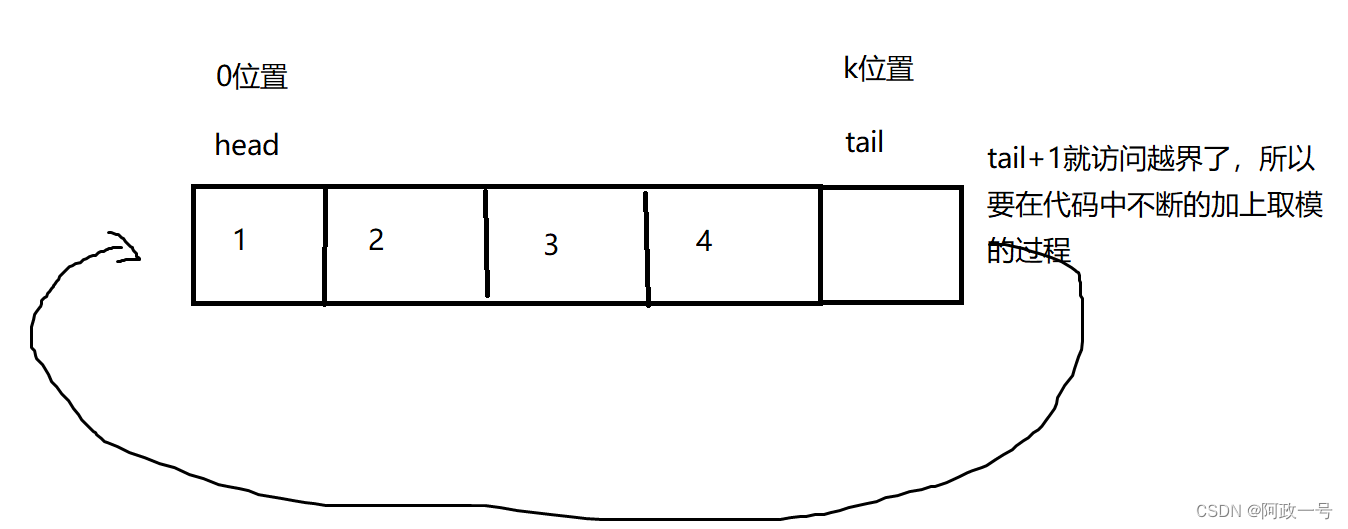
到这里这四个OJ题就结束了,感谢大家的观看,如有错误,还请多多指出。
这篇关于栈与队列OJ题【括号适配问题】【用队列实现栈】【用栈实现队列】【设计循环队列】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






