本文主要是介绍理解导数(x^n求导后nx^n-1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
以下都是为了方便理解
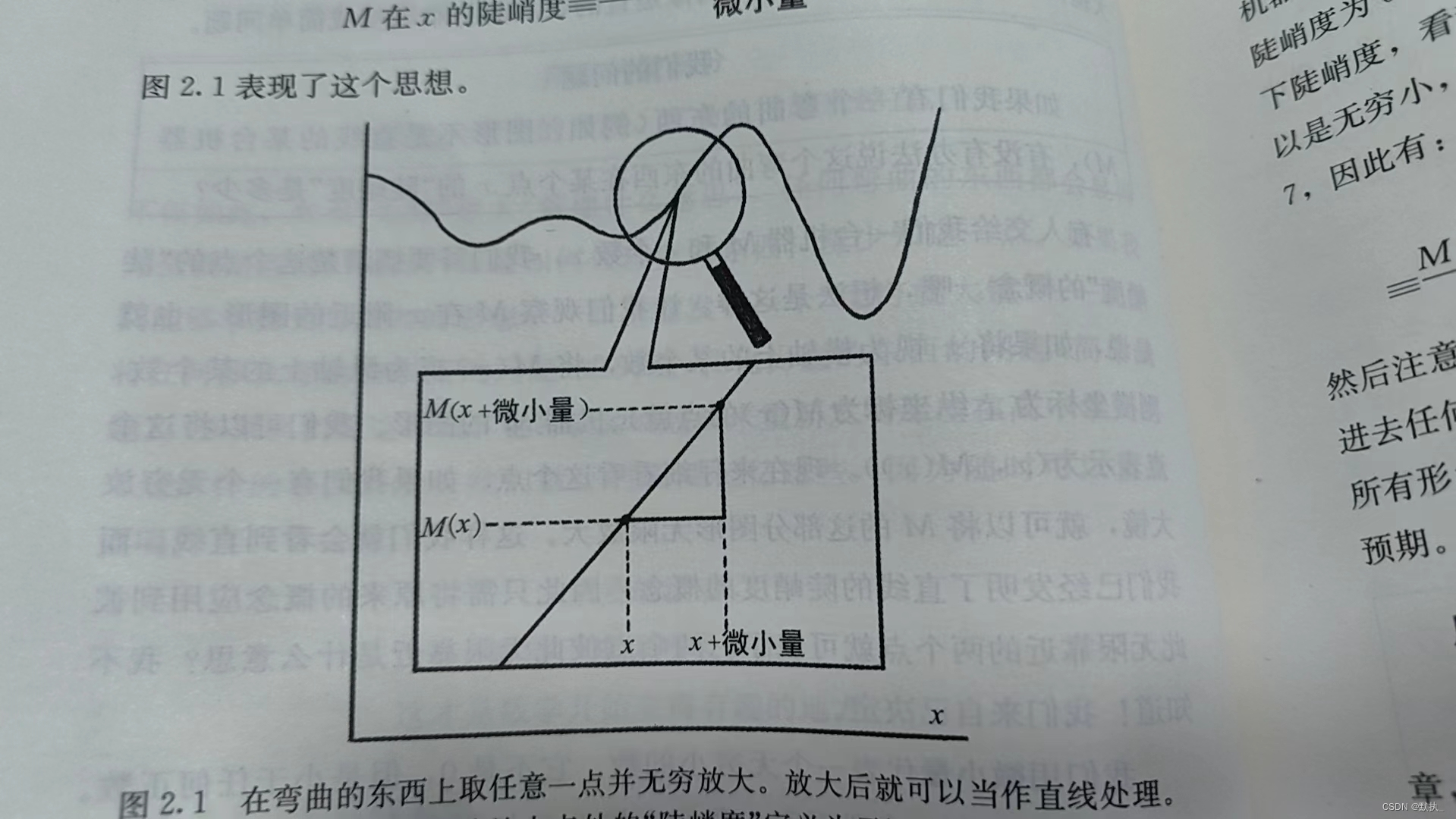
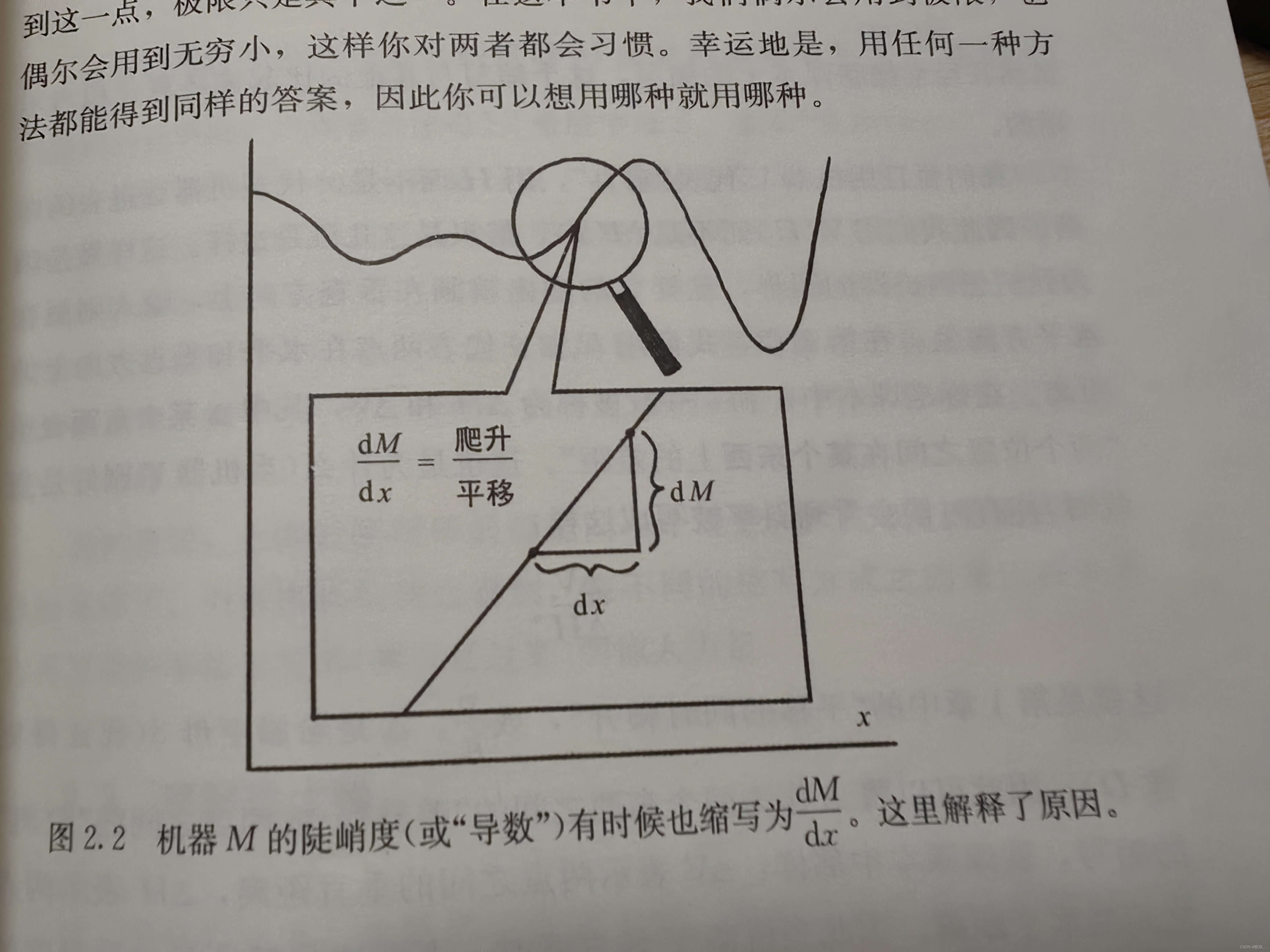
微小量是 t
M(x)是一个函数
M 在 x 处的斜率 = M 在 x 处的导数 = 垂直距离 平移距离 = M ( x + t ) − M ( x ) ( x + t ) − x M在x处的斜率 = M在x处的导数= \dfrac{垂直距离}{平移距离} =\dfrac{M\left( x+t\right) -M\left( x\right) }{(x + t) -x} M在x处的斜率=M在x处的导数=平移距离垂直距离=(x+t)−xM(x+t)−M(x)
求导原型 = M ( x ) = M ( x + t ) − M ( x ) t 求导原型=M\left( x\right) =\dfrac{M\left( x+t\right) -M\left( x\right) }{t} 求导原型=M(x)=tM(x+t)−M(x)
当前数的导数 = ( 当前数 + 微小量 ) − 当前数 微小量 当前数的导数 = \dfrac{(当前数 + 微小量) - 当前数}{微小量} 当前数的导数=微小量(当前数+微小量)−当前数
将直线方程带入,进行求导: M(x)= kx+b
[ k ( x + t ) + b ] − [ k x + b ] t = k ( t ) t = k \dfrac{\left[ k\left( x+t\right) +b\right] -\left[ kx+b\right] }{t} = \dfrac{k\left( t\right) }{t}=k t[k(x+t)+b]−[kx+b]=tk(t)=k
x^2
若x的变化规律是平方
M 在 x 点的导数 = M ( x + t ) − M ( x ) t = ( x + t ) 2 − x 2 t M在x点的导数 = \dfrac{M\left( x+t\right) -M\left( x\right) }{t} = \dfrac{\left( x+t\right) ^{2}-x^{2}}{t} M在x点的导数=tM(x+t)−M(x)=t(x+t)2−x2
根据平方和公式:
M 在 x 点的导数 = x 2 + 2 x ( t ) + ( t ) 2 − x 2 t = 2 x ( t ) + ( t ) 2 t M在x点的导数 = \dfrac{x^{2}+2x\left( t\right) +\left( t\right) ^{2}-x^{2}}{t} = \dfrac{2x\left( t\right) +\left( t\right) ^{2}}{t} M在x点的导数=tx2+2x(t)+(t)2−x2=t2x(t)+(t)2
M 在 x 的陡峭度 = 2 x + t M在x的陡峭度 = 2x+t M在x的陡峭度=2x+t
由于t可以忽略不记,所以最终结果是2x
x^3
M 在 x 点的导数 = M ( x + t ) − M ( x ) t = ( x + t ) 3 − x 3 t M在x点的导数 = \dfrac{M\left( x+t\right) -M\left( x\right) }{t} = \dfrac{\left( x+t\right) ^{3}-x^{3}}{t} M在x点的导数=tM(x+t)−M(x)=t(x+t)3−x3
根据立方和公式:
( x + t ) 3 = x 3 + t 3 + 3 x 2 t + 3 x t 2 (x + t )^{3} = x^{3} + t^{3} + 3x^{2}t + 3xt^{2} (x+t)3=x3+t3+3x2t+3xt2
M 在 x 点的导数 = x 3 + t 3 + 3 x 2 t + 3 x t 2 − x 3 t = t 3 + 3 x 2 t + 3 x t 2 t M在x点的导数 = \dfrac{x^{3} + t^{3} + 3x^{2}t + 3xt^{2} - x^{3}}{t} = \dfrac{t^{3} + 3x^{2}t + 3xt^{2}}{t} M在x点的导数=tx3+t3+3x2t+3xt2−x3=tt3+3x2t+3xt2
M 在 x 点的导数 = t 3 + 3 x 2 t + 3 x t 2 t = t 2 + 3 x 2 + 3 x t M在x点的导数 = \dfrac{t^{3} + 3x^{2}t + 3xt^{2}}{t} = t^{2} + 3x^{2} + 3xt M在x点的导数=tt3+3x2t+3xt2=t2+3x2+3xt
由于t可以忽略不记,所有最终结果:3x^2
M 在 x 点的导数 = t 2 + 3 x 2 + 3 x t = 3 x 2 M在x点的导数 = t^{2} + 3x^{2} + 3xt = 3x^{2} M在x点的导数=t2+3x2+3xt=3x2
x^n
到这里我们可以发现,展开(x+t)^n是最费力的。
找规律:
在展开(x+t)^n的时候,到后面 t 相互抵消后,总会留下来一个
n x n − 1 nx^{n-1} nxn−1
到现在为止我们知道了,对常数求导后结果是 0 ,对 x 的 n 次方求导结果是 n x n − 1 到现在为止我们知道了,对常数求导后结果是0,对x的n次方求导结果是nx^{n-1} 到现在为止我们知道了,对常数求导后结果是0,对x的n次方求导结果是nxn−1
就是下面两个红框的内容

导数求极值
示例:
f ( x ) = x 2 − 6 x + 9 f\left( x\right) =x^{2}-6x+9 f(x)=x2−6x+9
将上面例子求导
f ( x ) = 2 x − 6 f\left( x\right) = 2x-6 f(x)=2x−6
极值点通常在导数为0的点
0 = 2 x − 6 0 = 2x-6 0=2x−6
x = 3 x = 3 x=3
极值点是3
这篇关于理解导数(x^n求导后nx^n-1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





