本文主要是介绍随机梯度下降SGD的理解和现象分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
提出问题:令人疑惑的损失值
在某次瞎炼丹的过程中,出现了如下令人疑惑的损失值变化图像:

嗯,看起来还挺工整,来看看前10轮打印的具体损失值变化:
| epoch 1 | iter 5 / 10 | time 1[s] | loss 2.3137 | lr 0.0010
| epoch 1 | iter 10 / 10 | time 1[s] | loss 2.2976 | lr 0.0010
| epoch 2 | iter 5 / 10 | time 1[s] | loss 2.3135 | lr 0.0010
| epoch 2 | iter 10 / 10 | time 1[s] | loss 2.2973 | lr 0.0010
| epoch 3 | iter 5 / 10 | time 1[s] | loss 2.3132 | lr 0.0010
| epoch 3 | iter 10 / 10 | time 1[s] | loss 2.2970 | lr 0.0010
| epoch 4 | iter 5 / 10 | time 1[s] | loss 2.3129 | lr 0.0010
| epoch 4 | iter 10 / 10 | time 1[s] | loss 2.2968 | lr 0.0010
| epoch 5 | iter 5 / 10 | time 1[s] | loss 2.3127 | lr 0.0010
| epoch 5 | iter 10 / 10 | time 1[s] | loss 2.2965 | lr 0.0010
| epoch 6 | iter 5 / 10 | time 1[s] | loss 2.3124 | lr 0.0010
| epoch 6 | iter 10 / 10 | time 1[s] | loss 2.2962 | lr 0.0010
| epoch 7 | iter 5 / 10 | time 1[s] | loss 2.3122 | lr 0.0010
| epoch 7 | iter 10 / 10 | time 1[s] | loss 2.2960 | lr 0.0010
| epoch 8 | iter 5 / 10 | time 1[s] | loss 2.3119 | lr 0.0010
| epoch 8 | iter 10 / 10 | time 1[s] | loss 2.2957 | lr 0.0010
| epoch 9 | iter 5 / 10 | time 1[s] | loss 2.3116 | lr 0.0010
| epoch 9 | iter 10 / 10 | time 1[s] | loss 2.2954 | lr 0.0010
| epoch 10 | iter 5 / 10 | time 1[s] | loss 2.3114 | lr 0.0010
| epoch 10 | iter 10 / 10 | time 1[s] | loss 2.2952 | lr 0.0010
可以明显看到两列出现递减的子序列:奇数序列和偶数序列。奇数序列的损失值为2.3137, 2.3135, 2.3132, 2.3129,...;奇数序列的损失值为2.2976, 2.2973, 2.2970, 2.2968,...。事出反常必有妖,那么究竟是什么样的东西导致如此的怪象?
在尝试找具体的原因之前,我们先把涉及的具体参数描述清楚。
模型就是一个很简单的序列模型,其网络结构如下:
layers = [MatMul(W1), Sigmoid(), MatMul(W2), Sigmoid(), MSE()]
网络结构就是两层重复结构,单层为一个矩阵乘法层MatMul加上一个激活函数Sigmoid,两层计算完后用均方误差MSE计算损失值,其中参数W1,W2的赋值如下:
rn = np.random.randn
W1 = (rn(10, 1000)).astype(np.float32)
W2 = (rn(1000, 10)).astype(np.float32)
数据和标签的赋值如下:
x = (rn(1000, 10)).astype(np.float32)
t = x**2
数据就是按照正态分布随机化初始1000个10维的向量,而标签就是原来的向量按元素乘方,而炼丹的目的就是观察模型如何学习二次函数的运算法则的。
相关训练的参数如下:
epochs = 100
batch_size = 100
eval_interval = 5
lr = 0.001
训练一共进行100轮,每一轮的每一批数据有100个,对于1000个数据,那么单个轮次可以分10个批次。每个批次都会计算当前批次100个数据的平均损失值,5个批次评估一次平均损失值,然后打印出来。也就是单个轮次可以看到2次打印出来的评估数据。
显然,第1次评估的平均损失值是用前一半的数据计算出来的,而第2次的则是后一半的数据进行运算。那么可以简单猜测:造成如此令人困惑的损失值变化图像,很可能原因就在数据分批上。
本质思考:推导数学公式解释
我们先把模型抽象为数学上的函数 F F F,其具体形式如下:
L o s s = F ( x , t , w ) Loss = F(x,t,w) Loss=F(x,t,w)
其中, x x x为数据, t t t为标签, w w w为权重, L o s s Loss Loss为损失值。
考虑到数据分批,对数据分成 m m m批的情况,实际上存在 m m m个子函数,如下:
L 1 = F 1 ( x 1 , t 1 , w ) L 2 = F 2 ( x 2 , t 2 , w ) L 3 = F 3 ( x 3 , t 3 , w ) . . . L m = F m ( x m , t m , w ) \begin{matrix} L_{1} = F_{1} (x_{1},t_{1},w)\\L_{2} = F_{2} (x_{2},t_{2},w) \\L_{3} = F_{3} (x_{3},t_{3},w) \\... \\L_{m} = F_{m} (x_{m},t_{m},w) \end{matrix} L1=F1(x1,t1,w)L2=F2(x2,t2,w)L3=F3(x3,t3,w)...Lm=Fm(xm,tm,w)
如果将 w ( i , j ) w_{(i,j)} w(i,j)表示为第 i 轮 i轮 i轮第 j j j批的权重值,那么很显然对第 i i i轮的训练批次来说,存在如下关系:
w i , 0 = w i − 1 , m w i , 1 = w i , 0 + k ∂ F 1 ∂ w ∣ w = w i , 0 w i , 2 = w i , 1 + k ∂ F 2 ∂ w ∣ w = w i , 1 w i , 3 = w i , 2 + k ∂ F 3 ∂ w ∣ w = w i , 2 . . . w i , m = w i , m − 1 + k ∂ F m ∂ w ∣ w = w i , m − 1 \begin{matrix} w_{i,0}=w_{i-1,m}\\w_{i,1} = w_{i,0}+k\frac{\partial F_{1}}{\partial w}|_{w=w_{i,0}} \\w_{i,2} = w_{i,1}+k\frac{\partial F_{2}}{\partial w}|_{w=w_{i,1}} \\w_{i,3} = w_{i,2}+k\frac{\partial F_{3}}{\partial w}|_{w=w_{i,2}} \\... \\w_{i,m} = w_{i,m-1}+k\frac{\partial F_{m}}{\partial w}|_{w=w_{i,m-1}} \end{matrix} wi,0=wi−1,mwi,1=wi,0+k∂w∂F1∣w=wi,0wi,2=wi,1+k∂w∂F2∣w=wi,1wi,3=wi,2+k∂w∂F3∣w=wi,2...wi,m=wi,m−1+k∂w∂Fm∣w=wi,m−1
其中 k k k为学习率的相反数,且一般情况下取值都较小(如取 k = − 0.001 k=-0.001 k=−0.001)。考虑到 k k k取值较小,所以有如下近似公式:
w i , 0 = w i − 1 , m w i , 1 = w i , 0 + k ∂ F 1 ∂ w ∣ w = w i , 0 w i , 2 ≈ w i , 1 + k ∂ F 2 ∂ w ∣ w = w i , 0 w i , 3 ≈ w i , 2 + k ∂ F 3 ∂ w ∣ w = w i , 0 . . . w i , m ≈ w i , m − 1 + k ∂ F m ∂ w ∣ w = w i , 0 \begin{matrix} w_{i,0}=w_{i-1,m}\\w_{i,1} = w_{i,0}+k\frac{\partial F_{1}}{\partial w}|_{w=w_{i,0}} \\w_{i,2} \approx w_{i,1}+k\frac{\partial F_{2}}{\partial w}|_{w=w_{i,0}} \\w_{i,3} \approx w_{i,2}+k\frac{\partial F_{3}}{\partial w}|_{w=w_{i,0}} \\... \\w_{i,m} \approx w_{i,m-1}+k\frac{\partial F_{m}}{\partial w}|_{w=w_{i,0}} \end{matrix} wi,0=wi−1,mwi,1=wi,0+k∂w∂F1∣w=wi,0wi,2≈wi,1+k∂w∂F2∣w=wi,0wi,3≈wi,2+k∂w∂F3∣w=wi,0...wi,m≈wi,m−1+k∂w∂Fm∣w=wi,0
从而进一步得到如下具体的近似公式:
w i , j ≈ w i − 1 , j + ∑ t = 1 m k ∂ F t ∂ w ∣ w = w i − 1 , j w_{i,j} \approx w_{i-1,j}+\sum_{t=1}^{m} k\frac{\partial F_{t}}{\partial w}|_{w=w_{i-1,j}} wi,j≈wi−1,j+t=1∑mk∂w∂Ft∣w=wi−1,j
为了直观得到结论,采用如下表示:
v t = k ∂ F t ∂ w ∣ w = w i − 1 , j v_{t} = k\frac{\partial F_{t}}{\partial w}|_{w=w_{i-1,j}} vt=k∂w∂Ft∣w=wi−1,j
那么之前的表达式就可以简写为:
w i , j ≈ w i − 1 , j + ∑ t = 1 m v t w_{i,j} \approx w_{i-1,j}+\sum_{t=1}^{m} v_{t} wi,j≈wi−1,j+t=1∑mvt
对于 w i , j w_{i,j} wi,j来说, v j v_{j} vj才是其让损失值下降最快的方向,其他的向量代表其他批的数据,往往得到的方向与该方向比较随机,最后得到的和可能趋于0或者其他损失值下降不太快的方向。
因此,要想让第 j j j批的数据对应的损失值稳定下降,还得靠一轮一轮的循环才行,靠同一轮的其他批次是不太合理的(只有一部分情况才能如此)
合理外推:实验数据验证想法
如果看懂了前面的数学推导,那么很自然就能想到:对于批次 m m m较大的情况下,损失函数图像会呈现整体趋势下降的条带,如下图:

其中训练参数改动如下:
x = (rn(2000, 10)).astype(np.float32)
t = x**2
epochs = 200
你说啥?数学推导没看懂?那也没关系,其实到最后只是为了说明一个事情:你把训练数据分成很多个批次去炼丹,对于具体的某个批次的损失值下降,主要是依赖该批次的下一轮迭代,而不是同一轮的其他批次。
如果你感觉条带形状的损失值碍眼,感觉损失值起起伏伏的,很多计算资源都浪费了,那么用一招就能“瞒天过海”:把损失值的评估计算改为一整轮的平均损失,比如有 m m m批数据,那么统计损失值时使用这 m m m个批次的损失值总平均值即可,效果绝对立竿见影:
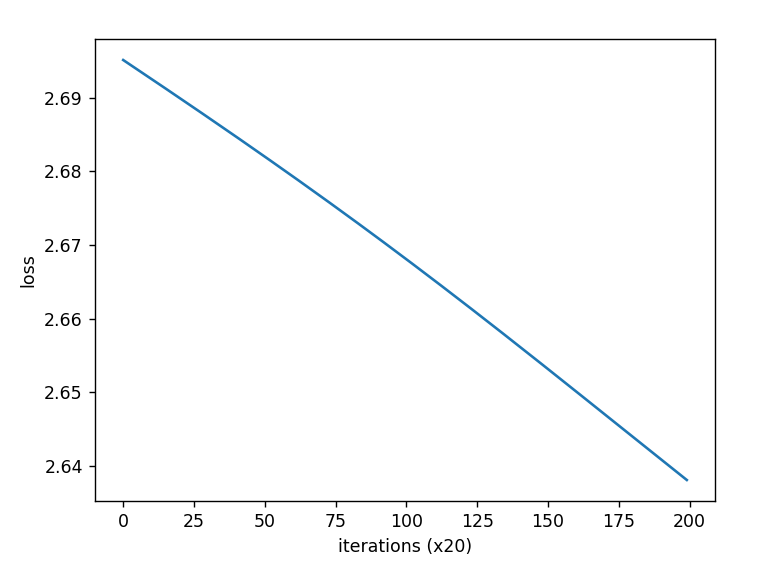
其中训练参数改动如下:
x = (rn(2000, 10)).astype(np.float32)
t = x**2
epochs = 200
batch_size = 100
eval_interval = 20
这参数里面,一共有2000个数据,100个数据为1批,共20批数据,然后20批数据评估一次整体平均损失值,训练200轮。
这篇关于随机梯度下降SGD的理解和现象分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





