本文主要是介绍CTF-reverse,逆向分析,对“左移4或右移4,即(x<<4) | (x >>4)的加密探讨,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
博主在刷题过程中遇上这样一个有意思的加密(如下图),苦苦思索其逆向运算,被硬控了很久,也没搜到什么资料来解释这个问题(也许是太简单??蒟蒻博主怀疑人生……)
经过博主不断猜想、写代码验证再配合已有的位运算知识,也算是总结出一些规律
直接先上结论:这个加密是(伪)对称加密,其解密就是加密本身!
此处的(伪)对称加密指的是,使用该函数加密、再解密的结果只有映射到ASCII表中才是对称的,即仅对字符数组满足对称加密
一,加密特征
本文标题其实已经揭露了该加密的特征,就是(x<<4) | (x >>4)
注意这里的4,很有可能被题目以其它等价运算的形式表现出来,例如<<4改成*16,>>4改成/16等等
博主目前只遇到过左右移4的情况,但经过测试发现,位移操作数若是(4,8,12,16,24)这里面的数,也满足对称加密,但要注意的是,左右移的操作数应为同一个数,即不能是(x<<4) | (x>>8)这样的情况(左右移争对的是两个不同的数)
(注:32也满足,但按照位移运算的定义,左右移32位对于32位整数来说相当于未操作,因此不列入)
结论:若f(x)=(x<<shift) | (x>>shift)且shift属于集合(4,8,12,16,24),则f(x)的结果映射到ASCII表(0,127)中是对称加密。
二,(伪)对称验证
#include <bits/stdc++.h>
using namespace std;
int func(int x) {int shift = 4;return (x << 8) | (x >> 8);//4,8,12,16,24
}
int main() {int x = 99;cout << "明文: " << x << " " << (char)x << endl;x = func(x); //加密cout << "密文: " << x << endl;x = func(x); //解密cout << "二次加密(伪明文): " << x << endl;cout << "伪明文%128: " << x % 128 << " " << (char)(x % 128) << endl; //将解密得到的伪明文%128(映射到ASCII码表)return 0;
}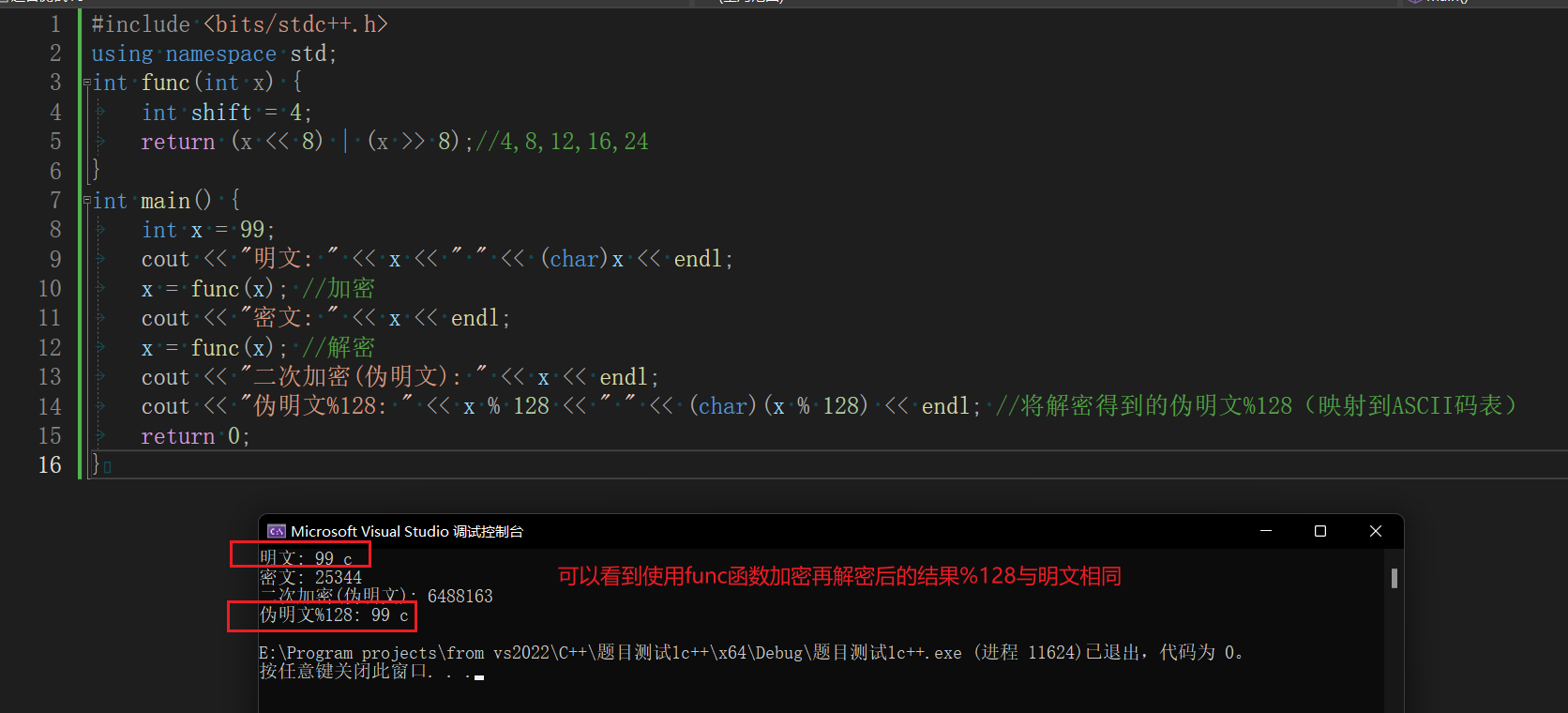
因此,在逆向分析过程中遇到满足此特征的加密,即可认为是(伪)对称加密,可直接使用原函数进行解密,但要牢记的是解密得到的结果应该%128(映射到ASCII码表)才是正确明文
三,证明过程
博主不是什么专业的密码学或数学学者,只能从位运算的本质出发,通过对比加解密后的结果与明文的差异来得出结论
(或运算的规则:同位有1则1,同位都0则0)
函数f(x)=(x<<4) | (x>>4)
明文: 0000 0000 0000 0000 0000 0000 0001 0000
①明文<<4: 0000 0000 0000 0000 0000 0001 0000 0000
②明文>>4: 0000 0000 0000 0000 0000 0000 0000 0001
①|②: 0000 0000 0000 0000 0000 0001 0000 0001 <-此时完成加密得到密文
c密文<<4:0000 0000 0000 0000 0001 0000 0001 0000
d密文>>4:0000 0000 0000 0000 0000 0000 0001 0000
c|d: 0000 0000 0000 0000 0001 0000 0001 0000 <-此时完成解密得到伪明文
此时我们重点关注被f(x)加密再解密的结果与明文的差异:
明文: 0000 0000 0000 0000 0000 0000 0001 0000
c|d: 0000 0000 0000 0000 0001 0000 0001 0000(伪明文)
明文的十进制值为16,伪明文的十进制值为4112,满足4112%128=16
从它们的二进制值也能直观看出,伪明文与明文仅差在第13位(红色部分),而128等于2的8次方,因此模128的结果只会剩下最后8位(绿色部分),也就和明文一致了
根据该思路,不难证明当shift属于集合(4,8,12,16,24)中的数时,均满足此规律,此处便不再赘述
这篇关于CTF-reverse,逆向分析,对“左移4或右移4,即(x<<4) | (x >>4)的加密探讨的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









