漫步数学分析三十九——隐函数定理

本文主要是介绍漫步数学分析三十九——隐函数定理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

假设$x,y$被方程$F(x,y)=0$关联起来，我们会说这定义了一个函数$y=f(x)$(或者说隐式定义了$y=f(x)$)，然后打算计算$dy/dx$。前面已经提到过，给定这样的$F$，一般不能显式求出$y$，所以在没有求解之前知道这样的函数存在是非常重要的。

为了更好的理解给出的结论，考虑函数$F(x,y)=x^2+y^2-1$，我们对满足$F(x,y)=0$的$x,y$感兴趣，该函数中就是单位圆，当且仅当$f$定义域中的所有$x$均满足$F(x,f(x))=0$ 时，函数$f(x)$有解。显然$f$形式肯定为$f(x)=\pm\sqrt{1-x^2}$，他们中有一个就是解，因此$f$不一定是唯一的。给定$(x_0,y_0)$满足$F(x_0,y_0)=0$，我们想知道是否我们能找到$f(x)$使得$F(x,f(x))=0$，$f$在$(x_0,y_0)$附近是可微且唯一的。如果$x_0\neq\pm1$，$f$取合适的平方根那么就可以。给定的$y_0$确定所选择的平方根，如图1所示，点$x=\pm1$比较特殊有几个原因。首先$f$在该处不可微，其次在$x_0=\pm1$附近它不是唯一确定的，这些地方就是$\partial F/\partial y=0$的地方，从而我们想要像$\partial F/\partial y\neq0$这样的条件来保证(至少是局部上)我们可以找到一个唯一的可以函数$f$使得$F(x,f(x))=0$。

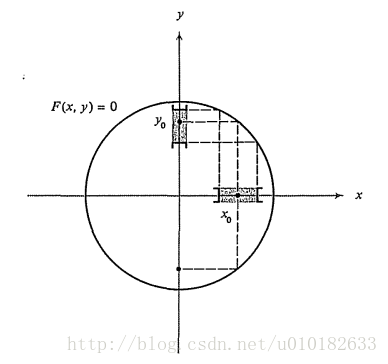
图1

一般情况下我们希望有一个函数$F:R^n\times R^m\to R^m$并且考虑关系$F(x,y)=0$，或者写成

$$\begin{matrix} F_1(x_1,\ldots,x_n,y_1,\ldots,y_m)&=&0\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \cdot&&\cdot\\ F_m(x_1,\ldots,x_n,y_1,\ldots,y_m)&=&0 \end{matrix}$$

我们想从这$m$个方程中用$x_1,\ldots,x_n$的形式求出$m$个未知变量$y_1,\ldots,y_m$。

定理如下。

$\textbf{定理2}$(隐函数定理) 令$A\subset R^n\times R^m$是一个开集并且$F:A\to R^m$是$C^p$类函数(即$F$有$p$ 阶连续导数，其中$p$是一个正整数)。假设$(x_0,y_0)\in A,F(x_0,y_0)=0$，

$$\Delta= \begin{vmatrix} \frac{\partial F_1}{\partial y_1}&\cdots&\frac{\partial F_1}{y_m}\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \frac{\partial F_m}{\partial y_1}&\cdots&\frac{\partial F_m}{y_m} \end{vmatrix}$$

在$(x_0,y_0)$处计算，其中$F=(F_1,\ldots,F_m)$。假设$\Delta\neq 0$，那么存在一个$x_0$的开邻域$U\subset R^n$与$y_0$的开邻域$V$与唯一的函数$f:U\to V$，它对所有的$x\in U$，满足

$$F(x,f(x))=0$$

更进一步，$f$是$C^p$类。

实际上我们应该看出上面的定义可以从逆函数中推出，从上面的例子可以看出该定理的有效性以及限制条件$\Delta\neq 0$ 的必要性，从方程$F(x,f(x))=0$中我们可以用链式法则确定$Df$。首先考虑$m=1$的情况，那么根据链式法则

$$0=\frac{\partial}{\partial x_i}F(x,f(x))=\frac{\partial F}{\partial x_i}+\frac{\partial F}{\partial y}\frac{\partial f}{\partial x_i}$$

所以我们得到一个重要的方程(注意负号)：

$$\frac{\partial f}{\partial x_i}=-\frac{\partial F/\partial x_i}{\partial F/\partial y}$$

这里需要特别提醒一下，对于

$$\frac{(\partial F/\partial x_i)}{(\partial F/\partial y)}$$

不能够消去$\partial F$得出$\partial y/\partial x_i$。

我们可以像上面那样形式化一般的解。

$\textbf{推论1}$ 在定理2中，$\partial f_j/\partial x_i$形式为

$$\begin{pmatrix} \frac{\partial f_1}{\partial x_1}&\cdots&\frac{\partial f_1}{\partial x_n}\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \frac{\partial f_m}{\partial x_1}&\cdots&\frac{\partial f_m}{\partial x_n} \end{pmatrix} =- \begin{pmatrix} \frac{\partial F_1}{\partial y_1}&\cdots&\frac{\partial F_1}{\partial y_m}\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \frac{\partial F_m}{\partial y_1}&\cdots&\frac{\partial F_m}{\partial y_m} \end{pmatrix}^{-1} \begin{pmatrix} \frac{\partial F_1}{\partial x_1}&\cdots&\frac{\partial F_1}{\partial x_n}\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \cdot&&\cdot\\ \frac{\partial F_m}{\partial x_1}&\cdots&\frac{\partial F_m}{\partial x_n} \end{pmatrix}$$

其中$e^{-1}$表示逆矩阵。

该推论的证明与上面介绍的$m=1$情况一样。

$\textbf{例1：}$考虑方程组

$$\begin{align*} xu+yv^2&=0\\ xv^3+y^2u^6&=0 \end{align*}$$

在$x=0,y=1,u=0,v=0$附近用$x,y$表示的$u,v$解是唯一的吗？如果$\partial u/\partial x$在$x=0,y=1$处有解，那么求出该解。

$\textbf{解：}$这里我们有$F(x,y,u,v)=0$，其中$F$表示给定方程的左半边，我们想看是否能求解$u(x,y),v(x,y)$，从而

$$\Delta= \begin{vmatrix} \frac{\partial F_1}{\partial u}&\frac{\partial F_1}{\partial v}\\ \frac{\partial F_2}{\partial u}&\frac{\partial F_2}{\partial v} \end{vmatrix}= \begin{vmatrix} x&2yv\\ 6y^2u^5&3xv^2 \end{vmatrix}$$

在给定的点处它等于0，隐函数定理告诉我们我们不能用$x,y$唯一的求出$u,v$。

to be continue……

这篇关于漫步数学分析三十九——隐函数定理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---