本文主要是介绍2024深圳杯A题高质量无水印23页成品论文【附带Q1-Q4完整代码解答】+持续更新,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
A题基于优化模型的多个火箭残骸的准确定位
部分内容展示
【无水印word】2024深圳杯A题成品论文23页+mtlab(python)双版本代码![]() https://www.jdmm.cc/file/2710565
https://www.jdmm.cc/file/2710565

5.2 问题二三模型的建立与求解
5.2.1 数据分析
声波从音爆源到监测设备的传播是一个球面波,其半径随时间增加而扩大。对于每个残骸,它在空中发生音爆时会产生一个扩散的声波球。与问题一给出数据相同,为了更加直观的展示给出数据,首先以A为例绘制了二维平面、三维平面的声波球。
图1设备A位置可视化
以这种方式引入更多的设备绘制可视化结果,如下所示
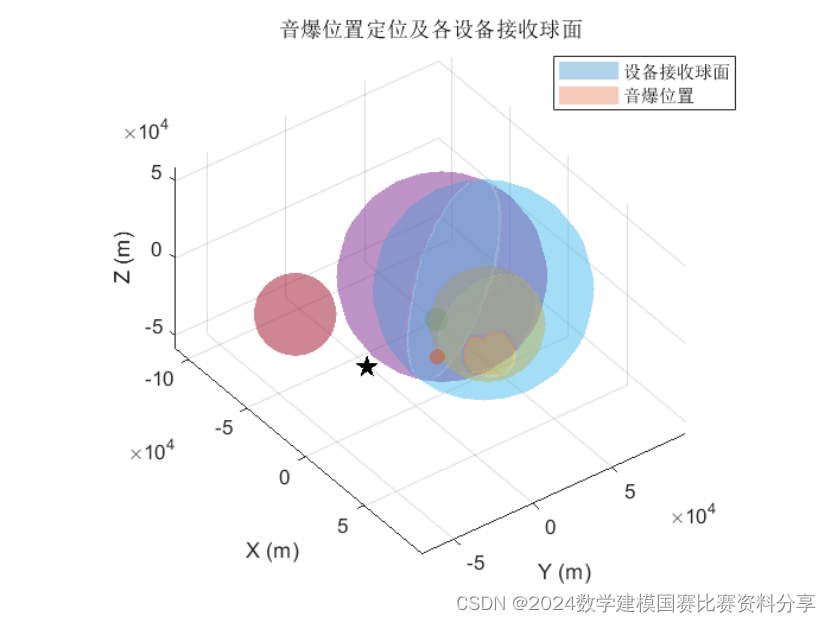
图1多设备可视化
5.2.2 多个残骸定位模型的建立
声波从音爆源到监测设备的传播是一个球面波,其半径随时间增加而扩大。对于每个残骸,它在空中发生音爆时会产生一个扩散的声波球。可以使用多边测量(triangulation)原理,根据多个监测站接收到的声波到达时间来定位每个音爆源的位置。通过比较不同监测站接收到的声波时间,可以使用时间差定位(Time Difference of Arrival, TDOA)方法来确定每个残骸的位置。
为了确定三维空间中一个点的位置,至少需要从四个不同的位置测量(四台设备),但由于存在四个残骸,这就要求至少需要五个监测站以确保可以解出一个唯一的解集(这是因为每增加一个音爆源,就需要一个额外的监测站来提供独立的测量)。使用非线性最小化算法来解决多变量的优化问题,以找到四个残骸的最可能位置和时间。
时间差定位(Time Difference of Arrival,TDOA)是一种基于时间测量来确定信号源位置的方法。在给定的问题中,这个原理可以用来确定火箭残骸发生音爆时的位置。以下是TDOA的基本原理
假设有多个监测站(至少三个)围绕一个音爆源。当音爆发生时,声波会从源点向外以声速传播。由于监测站与音爆源之间的距离不同,每个监测站接收到声波的时间也会有所不同。
因此,每个监测站都可以提供一个与音爆源的距离成正比的时间测量值。通过至少三个这样的测量,可以建立一个方程组来解决未知的音爆发生位置。由于监测站接收到信号的实际时间都是已知的,可以通过比较不同监测站接收到信号的时间差来建立方程组。这些方程是关于音爆源位置的非线性方程,因为它们包含了未知数的平方和开方运算。
为了确定唯一的音爆源位置,需要解决这个方程组。通常,这会通过数值方法来完成,因为解析解可能不存在或者难以得到。通过最小化每个方程的误差平方和,可以用数值优化方法(如最小二乘法)来求解这个问题。
在有多个音爆源的情况下,如火箭的多个残骸,每个残骸都会产生一个类似的方程组。需要同时解决所有的方程组,并且考虑各个方程组之间的关系,这样才能确定每个残骸的位置和音爆时间。这通常需要一个更复杂的数值算法,并可能涉及到多变量和多目标优化。
具体模型如下所示
给定监测设备的地理坐标
以及它们记录的各个残骸音爆抵达时间
(其中i 是设备索引,j是残骸索引),目标是确定每个残骸的空间位置
和音爆发生时间
。
设声速为常数c。将设备的地理坐标转换为笛卡尔坐标
后,目标函数可以表示为所有预测时间与实际时间差异的平方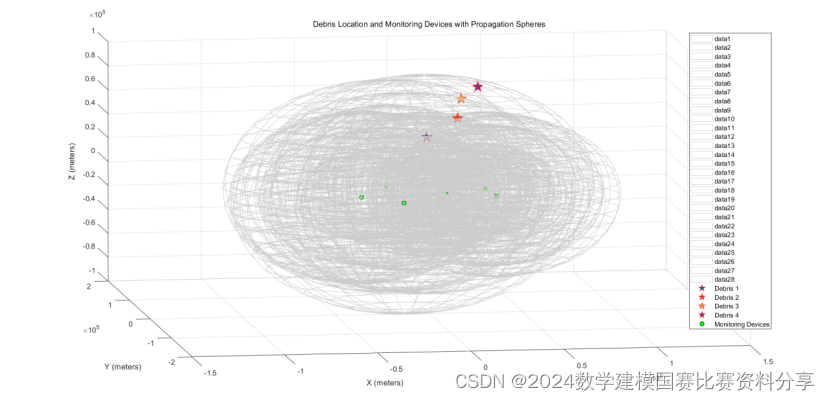
其中,
- v 是包含x,y,z,t 的向量。
- t 是音爆发生时间。
- (x,y,z) 是音爆发生的位置。
- c 是声速。
- (xi,yi,zi,ti) 是第 i 个设备的坐标和音爆抵达时间。
- n 是设备数量。
目标是最小化f(v),即预测时间和实际时间的平方差的和。
时间差约束
要考虑的一个约束是所有残骸音爆发生的时间差不能超过 5 秒。在目标函数中,可以通过对超过 5 秒的时间差引入较大的惩罚值来实现
如果
考虑到火箭残骸的速度范围,可以设置一个关于速度的约束。设
为残骸的最大可能速度,那么对于每个残骸 j,其位置变化率应该满足以下条件
其中,
分别是残骸 j在x,y,z 方向上的速度分量
高度约束
如果残骸的预期下落轨迹是已知的,可以设定一个高度范围 [min,max]。对于每个残骸 j,其高程应该满足
这样可以确保解决方案符合预期的飞行轨迹。
声速随高度变化的模型
声速 c 在不同的环境条件下会有所不同,特别是随高度的变化。可以引入一个关于高度的声速变化模型c(z)。音爆到达时间tij的计算公式应更新为
这里,积分沿着从残骸 j 到监测站 i 的路径计算,ds 是路径元素,c(z) 是在该路径上某点的声速。
考虑风速和风向的影响
考虑风速vwind和风向对声波传播的影响,残骸到监测站的实际声波传播时间 tij应考虑风的影响
其中uij是从残骸 j 指向监测站 i 的单位向量,点乘表示向量点乘,用于计算风速在声波传播方向上的投影。
最终建立优化模型,如下所示
5.2.3 模型的求解
差分进化(Differential Evolution, DE)算法是一种非常有效的全局优化算法,广泛用于解决实际中的优化问题,特别是那些参数优化问题。它基于群体的进化策略,通过对候选解进行交叉、变异和选择来寻找全局最优解。下面是差分进化算法的基本实现过程
- 初始化
种群初始化随机生成一个初始种群。种群中的每个个体(向量)代表一个可能的解。
参数设置设定算法的控制参数,包括变异因子(F)、交叉率(CR)和种群大小(NP)。
- 变异
对于种群中的每一个个体确保它们各不相同且不同。生成变异向
其中 F 是一个正的缩放因子,用于控制变异的强度。
- 交叉
为了增加种群的多样性,通过交叉操作生成试验向量
,对于的每个维度j
其中rand(j) 是在 [0,1] 上均匀分布的随机数,CR 是交叉概率,D 是个体的维数rand(1,D) 确保至少有一个维度来自变异向量。
- 选择
通过贪婪策略对每个个体进行评价和选择。如果试验向量的适应度(即目标函数值)比当前个体更好或相等,则在下一代种群中替换其中 t 表示当前的代数。
- 迭代
重复变异、交叉和选择步骤,直到满足停止条件(如达到最大迭代次数、达到预设的适应度阈值或解的改善不再显著)。
这里设定最大迭代次数为10000,这个参数设定了算法运行的最大代数,防止算法无限运行。
种群大小20,即在每一代中有多少个候选解参与迭代。较大的种群可以提供更多的多样性,但会增加计算成本。
容忍度为0.1,用于控制算法的停止条件之一,如果种群的标准偏差小于 tol 乘以规模,且连续几代没有改进,则停止迭代。
变异因子的范围(0.5, 1)。这是一个元组,定义了用于生成差分权重的下限和上限。变异因子控制了变异的程度,较高的变异因子可以增加多样性。
重组(或交叉)概率0.8。定义了从变异向量中选择参数的概率,较高的值增加了解空间的搜索范围,但可能减慢收敛速度。
最终得到结果如下所示
为了更加直观地展示可视化结果,绘制了三维可视化图进行展示
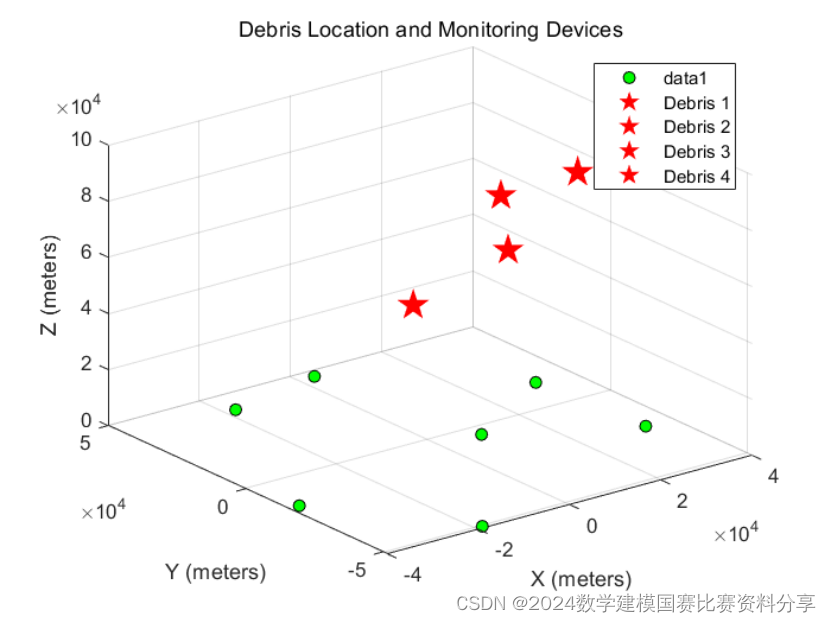
经过优化算法处理后,得出的四块残骸的位置分散在三维空间的不同点上.
这篇关于2024深圳杯A题高质量无水印23页成品论文【附带Q1-Q4完整代码解答】+持续更新的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






