无偏扭曲区域采样在可微分渲染中的应用

本文主要是介绍无偏扭曲区域采样在可微分渲染中的应用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

图1. 可微渲染计算光传输方程的导数。为了处理可见性的存在，最近的基于物理的可微渲染器需要显式地找到边界点[Li等人2018; Zhang等人2020]，或者通过启发式方法近似边界贡献[Loubet等人2019]。我们从第一原理出发，开发了一个无偏估计器，通过内部（区域）样本计算边界贡献。我们的方法可以轻松地与现有的重要性采样方法集成，并计算准确且低方差的梯度。例如，边缘采样方法[Li等人2018]发现很难一致地采样软反射中对导数有贡献的边界点，尤其是因为场景的复杂性很高。另一方面，我们的方法使用来自标准路径追踪器的样本，并利用BSDF和光源重要性采样来计算导数的稳健估计。我们通过与向上移动的有限差分图像进行比较，验证了我们的导数，其中使用了相同数量的样本。
可微渲染计算光传输方程关于任意3D场景参数的导数，并使反向渲染和机器学习等各种应用成为可能。我们提出了一种无偏且高效的可微渲染算法，不需要显式边界采样。我们将散度定理应用于渲染积分的导数，将边界积分转换为区域积分。我们将转换后的区域积分重写为适合蒙特卡罗渲染的形式。然后，我们开发了一个高效的蒙特卡罗采样算法来解决区域积分。我们的方法可以轻松插入到传统的路径追踪器中，不需要专门的数据结构来采样边界。
我们通过偏差-方差指标分析收敛性质，并展示了我们估计器在一些合成反向渲染示例中相对于现有方法的优势。
其他关键词和短语：逆向图形学、可微渲染、光传输、微分可见性

1 引言

可微渲染——计算光传输方程[Kajiya 1986]关于场景参数（如相机位置、三角网格位置和纹理参数）的导数的任务，对于解决反向渲染问题和训练3D深度学习模型变得越来越重要。由可见性引入的不连续性构成了一个核心挑战。

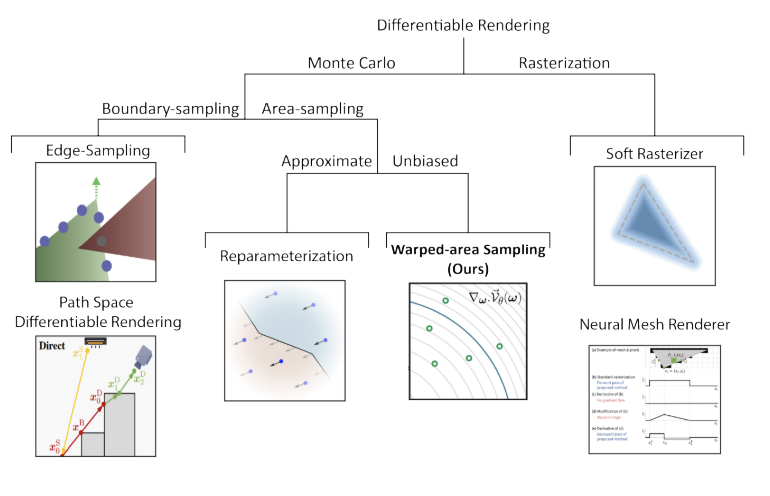
图2. 可微渲染的分类。两种边界采样技术都依赖于复杂的重要性采样数据结构。Li等人[2018]使用6D Hough树来寻找轮廓，而Zhang等人[2020]则预计算一个时空角度的光子图来找到重要的片段。相比之下，重参数化方法（Loubet等人[2019]）是轻量级的，只需要在标准蒙特卡罗渲染过程中实时计算一个旋转，但它是有偏差的。我们的方法保持了重参数化方法的简单性和灵活性，同时解决了它的偏差问题。
由于它们的导数测度为零，无法通过传统的蒙特卡罗方法进行采样，因此不连续性是可微渲染的挑战。已经提出了各种方法来解决可见性问题。我们将它们大致分为三类（图2）：
• 光栅化。许多确定性的可微光栅器通过忽略更高阶的传输（如阴影和全局照明）来近似可见性（例如[Kato等人2018; Loper和Black 2014]）。
• 边界采样。这些方法[Li等人2018; Zhang等人2020, 2019]显式地对出现在物体轮廓上的不连续性进行积分。它们可以无偏差地计算像素颜色相对于场景参数的梯度，同时考虑更高阶的传输。
• 区域采样。Loubet等人[2019]通过在一个单向路径追踪器中追踪辅助射线，并通过启发式方法检测轮廓，提出了一种边界采样的快速近似方法，通过采样区域而不是轮廓。然后他们通过旋转积分域来消除不连续性，对积分进行重参数化。
边界采样方法虽然产生了无偏差的结果，但在实现上通常更为复杂，效率较低，因为它们不能依赖传统渲染器中传统的立体角采样基础设施。对于主可见性，给定一个摄像机位置，3D对象的轮廓可以预先计算。然而，对于次级可见性，给定一个着色点，从对象的轮廓进行采样在计算上具有挑战性，需要进行昂贵的数据结构查询来找到轮廓[Hertzmann和Zorin 2000; Li等人2018; Olson和Zhang 2006; Sander等人2000]。此外，边界采样方法首先在边缘上采样点，然后将它们连接到其他光路顶点。这种连接使得特别具有挑战性。
另一方面，所有当前的非边缘采样方法都是有偏差的，不会收敛到目标解。
我们提出了一种使用区域采样的简单实用的可微渲染解决方案。通过从第一原理推导区域积分，我们展示了一种高效、一致的导数估计器，以及一种产生无偏差估计的版本。类似于Loubet等人的方法，我们的方法不需要专门的数据结构来选择轮廓边缘，可以通过追踪辅助射线轻松集成到传统的单向路径追踪器中。与Loubet等人的方法不同，我们的方法不会对积分引入近似，并产生一致或无偏差的估计。
我们的关键洞察是，我们可以应用散度定理，将对象轮廓上的积分转换为区域积分。我们表明，只要区域积分的最终被积函数是连续的，并且在边界上与轮廓积分的值匹配，那么这两个积分就是等价的。我们还表明，在这种解释下，Loubet等人的方法引入了偏差，因为对于这两个积分，轮廓处的被积函数不匹配。
给定连续性和边界条件，有无数的函数满足这些约束。然而，由于我们希望避免边界采样，我们正在解决一个困难的边界插值问题，没有事先知道边界，同时必须匹配边界处的贡献。为了解决这个问题，我们通过卷积一个边界匹配但有间断的场来构造一个平滑的区域积分。我们设计卷积，使其收敛到边界处贡献的值。然后，我们开发了一种采样算法，以产生对这个卷积的一致估计，并使用俄罗斯轮盘反偏差技术1来产生无偏差版本。我们还采用了对抗性采样和控制变量来减少卷积引入的方差。
实验表明，我们的采样算法引入了与Loubet等人方法相当的方差，但使用我们的一致估计器时几乎没有偏差（使用我们的无偏差版本时会减少到零）。这导致了在反向渲染问题中更准确的估计，而没有边缘采样方法的额外计算开销。
我们的贡献是：
• 我们通过应用散度定理，将可微渲染中出现的轮廓积分与传统渲染方程中的区域积分联系起来。
• 我们通过卷积识别出一组有用的区域积分，用于处理可微渲染中的不连续性。
• 我们推导出一种高效实用的算法来采样这些区域积分。我们的方法可以很容易地插入到一个单向路径追踪器中。

2 相关工作

光路导数。在光传输模拟中，关于光路参数的导数经常被渲染算法用于指导采样和重构[Arvo 1994; Chen和Arvo 2000; Mitchell和Hanrahan 1992; Ramamoorthi等人2007; Shinya等人1987; Ward和Heckbert 1992; Wu等人2020]。在最近的工作中，导数被用于马尔可夫链蒙特卡罗算法中，用于指导变异[Hanika等人2015; Jakob和Marschner 2012; Kaplanyan等人2014; Li等人2015; Luan等人2020; Rioux-Lavoie等人2020]。相比之下，我们感兴趣的是计算光传输贡献关于任意参数的导数，包括场景参数，如相机姿态和三角形顶点位置。
图形和视觉中的可微渲染。在图形和视觉社区中，对一种通用的可微渲染器有着强烈的需求。早期的图形和视觉算法经常使用专门的可微渲染器来解决其特定的逆图形问题（例如[Blanz和Vetter 1999; Jalobeanu等人2004; Patow和Pueyo 2003; Smelyansky等人2002]）。在机器学习框架中包含一个可微渲染层的兴趣也在增加（例如[Aittala等人2016; Genova等人2018; Li等人2019; Liu等人2017]）。
第一批通用的可微渲染器专注于近似主可见性，并支持有限的材料模型集[de La Gorce等人2011; Kato等人2018; Liu等人2019; Loper和Black 2014; Rhodin等人2015]。
可微光传输算法。最近，Li等人[2018]提出了第一个无偏差的蒙特卡罗解决方案，用于计算像素颜色关于场景参数的梯度。除了正确计算关于局部照明和相机投影的梯度外，他们的方法还适用于高阶传输现象，如阴影和全局照明。他们观察到，在像素预滤波后，平均像素颜色会连续地随着几何参数的变化而变化，使得渲染操作变得可微。Zhang等人[2020; 2019]进一步将该想法推广到处理参与介质和路径空间渲染。Nimier-David等人[2020]推导出一种新的微分光传输公式，通过从相机到光源传播导数量来减少内存需求。我们的方法可以与Nimier-David等人的公式一起使用，以处理可见性梯度。
Li等人的方法通过显式地采样Dirac delta信号来找到形成3D场景轮廓的边缘，这些信号出现在对积分内部的不连续性进行微分时。然而，这给采样基础设施引入了显著的开销。为了提高效率，Loubet等人[2019]提出了一种不要求在边缘上采样点的近似算法，而是通过由启发式构建的旋转矩阵对积分进行重参数化。他们的方法比Li等人的边缘采样具有更低的方差，但代价是增加了偏差，这可能对随机梯度优化产生显著影响。
我们的方法结合了边缘采样和区域采样方法的优点，实现了无偏差和高效性。更重要的是，我们展示了区域采样本身可以实现无偏差的结果。这使我们能够使用一个普通的单向路径追踪器来采样轮廓积分，而不需要昂贵的边缘选择过程，同时保持正确性。
敏感性分析。在粒子传输文献中，Roger等人[2005]推导出了具有变形域的积分的微分蒙特卡罗估计器。他们还认识到边界积分和区域积分之间的关系。然而，他们通过最小化Dirichlet能量来插值边界速度。这种策略在我们的情况下不适用，因为最小化需要明确列举边界，而这是我们首先想要避免的。

3 可微渲染的区域公式

我们的目标是为了计算渲染方程的导数，开发一种一致或无偏差的区域基采样方法。我们通过应用一个向量微积分的恒等式（散度定理）来将边界积分重构为由我们称为变形场的向量场补充的内部积分，从而实现了这一点。我们展示了变形场需要是连续的，并且与边界点的导数一致。然后，我们选择一个特定的变形场族，它只依赖于渲染积分上下文中可轻松获得的量。
在第4节中，我们展示了通过在每次反弹时追踪辅助射线来构造变形场的估计，从而可以增强一个单向路径追踪器来采样转换后的区域积分。

3.1 可微渲染中的边界积分

我们的目标是为了计算渲染积分的梯度：
𝐼 = ∫𝐷 𝑓(𝜔; 𝜃)d𝜔，（1）
对于某个域𝐷（例如半球域），其中函数𝑓依赖于一些场景参数𝜃，如三角形顶点位置或材料参数。对于可微渲染，我们感兴趣的是导数𝜕𝜃𝐼。
如先前的工作[Li等人2018]所示，直接使用𝜕𝜃𝑓(x, 𝜃)进行蒙特卡罗采样不是无偏差的，因为𝑓关于𝜃是不连续的，导数包括Dirac delta信号。相反，我们需要重写积分以消除Dirac deltas，以便使用基于区域的采样进行蒙特卡罗积分。

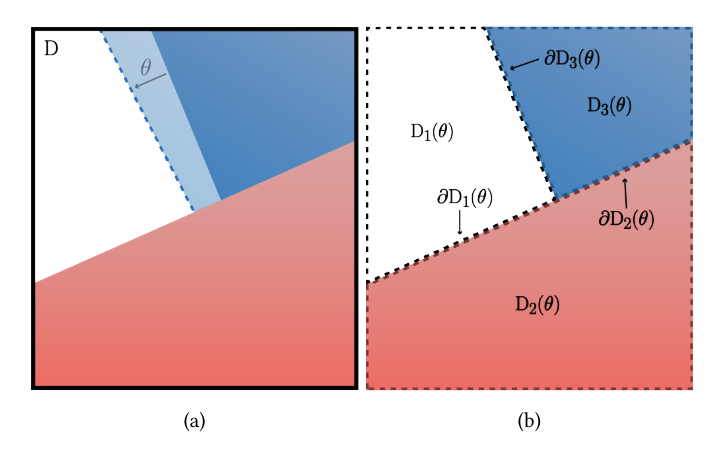
图3. 对边界移动进行微分。我们的目标是计算域D内平均颜色关于某个几何参数𝜃的导数。(a)显示了像素的几何内容示例，(b)说明了我们如何将域D划分为不相交的区域，使得所有不连续点都在边界𝜕D𝑖(𝜃)上。然后，在计算积分内部的不连续函数的导数时，我们可以适当地考虑边界的变化。
为了形式化这个过程，我们从之前的可微渲染工作[Li 2019; Zhang等人2019]中获得灵感，将域𝐷划分为不相交的区域𝐷0(𝜃)、𝐷1(𝜃)、𝐷2(𝜃)等，使得𝑓(𝑥; 𝜃)在每个区域的边界内是连续的，并且所有不连续点都在域的边界上（图3）。因此，域𝐷𝑖依赖于场景参数𝜃：
𝜕I/𝜕𝜃 = Σ𝑖 𝜕/𝜕𝜃 ∫Di(𝜃) 𝑓(𝜔; 𝜃)d𝜔。（2）
重要的是，这种划分只是为了我们的推导，我们不会显式地裁剪几何体来形成划分。
现在积分中的被积函数是连续的，我们可以通过对域𝐷𝑖(𝜃)的边界关于参数𝜃的变化进行测量，来重写微分积分。在一维空间中，这是莱布尼兹积分法则，可以从微积分基本定理（𝜕/𝜕𝜃 ∫𝑏(𝜃) 0 d𝑥 = 𝜕𝜃𝑏(𝜃)）推导出来。在高维空间中，这由雷诺兹输运定理[1903]（见Flanders [1973]的文章，其中有一个更短的证明）描述，该定理广泛应用于流体力学中出现的积分，其中流体流动会膨胀或收缩。雷诺兹输运定理的定义直接给出：
𝜕I/𝜕𝜃 = Σ𝑖 ∫D′i(𝜃) (𝜕𝑓(𝜔; 𝜃)/𝜕𝜃) dD′i(𝜃) + Σ𝑖 ∮𝜕Di(𝜃) 𝑓(𝜔; 𝜃) (𝜕𝜃𝜔·nˆ)d𝜕D𝑖(𝜃)（3）
其中第二项描述了域在边界𝜕D𝑖上的元素处的膨胀或收缩速率，第一项考虑了𝑓的连续部分，D′𝑖 = D𝑖 - 𝜕D𝑖。nˆ是边界处指向外侧的法向量。我们将第一项称为内部导数积分，第二项称为边界导数积分。

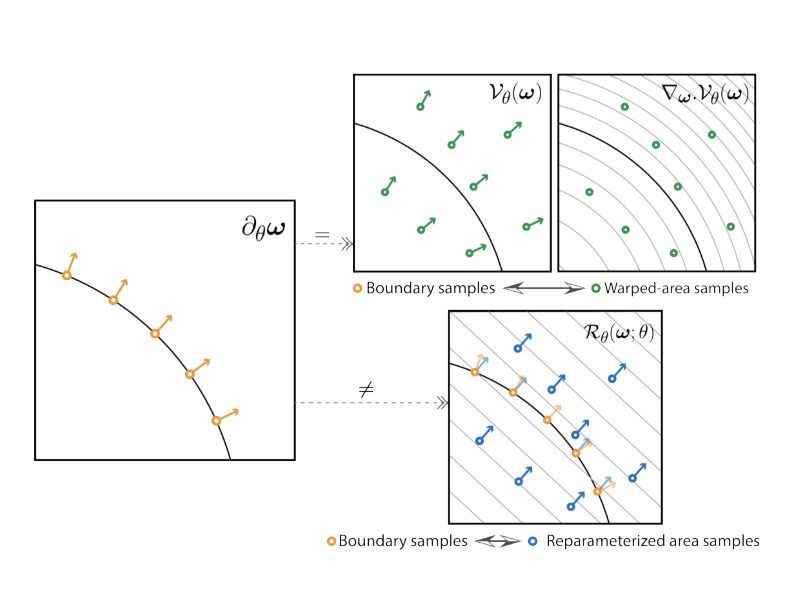
图4. 变形场公式。我们应用散度定理，该定理显示了雷诺兹输运定理的边界积分和我们的区域积分之间的等价性。该定理将边界𝜕𝜃𝜔的流出通量与域上的变形场V®𝜃(x)的散度联系起来。与重参数化技术[Loubet等人2019]不同，它使用均匀旋转来重参数化域，我们的方法产生一个空间变化的变形，对于这种等价性成立。这引入了一个散度项，直观地将边界贡献移动到导数的内部，在那里可以使用标准蒙特卡罗渲染进行计算。

3.2 边界导数积分的区域形式

由于在引言中提到的边界积分，方程3对于渲染积分来说很难求值。我们希望避免为边缘采样而设计的专用数据结构，并高效地采样镜面反射上的不连续点。此外，由于路径追踪是一个递归积分，在方程3中求值𝑓(𝑥; 𝜃)需要追踪完整的路径，使得边界采样的路径追踪成本与路径深度的平方成正比。
渲染社区已经研究了几十年来计算内部积分的高效技术。很自然地探索使用内部样本计算边界贡献的方法。我们通过直接将边界积分转换为区域积分来推导我们的解决方案，从而实现了一致性和无偏性。
关键的想法是应用散度定理，这是向量微积分中的一个基本结果。
散度定理（高斯-奥斯特罗格拉德斯基）。几个向量微积分的结果（格林定理、散度定理、斯托克斯定理）将边界积分与内部积分联系起来：
∮𝜕A f · nds = ∬A-𝜕A ∇𝜔 · fd𝜔。（4）
在许多应用中，散度定理和类似的向量微积分恒等式被用于将区域积分减少到边界积分，因为它减少了测度的维度并提供了计算上的好处（例如[Arvo 1995]）。相反，为了实现我们的目标，我们需要做相反的事情，找到一个与方程3中的边界项等价的区域积分。此外，雷诺兹输运定理将边界的贡献限制在法线方向上。这使我们能够忽略更一般的斯托克斯定理中出现的旋度项，而只计算散度。
我们应用散度定理（方程4）来重写与内部导数积分相同域中的边界导数积分：
I𝐵 = ∮𝜕D 𝑓(s; 𝜃) (𝜕𝜃s · nˆ) d𝑠 = ∬D′ ∇𝜔 · (𝑓(𝜔; 𝜃)V®𝜃(𝜔)) d𝜔 = ∬D′ (𝜕𝜔 𝑓(𝜔; 𝜃)) · V®𝜃(𝜔)d𝜔 + ∬D′ (∇𝜔 · V®𝜃(𝜔)) 𝑓(𝜔; 𝜃)d𝜔,（5）

其中变形场V®𝜃(x)是边界速度𝜕𝜃s的平滑插值。最后一个等式是由于散度的性质，我们将其包括在我们稍后将设置的蒙特卡罗估计中。图4说明了圆形边界的变形场的几何形状。
满足该方程的变形场有无数多个。根据散度定理的标准，我们可以看到变形场需要满足以下条件：
(1) (连续性) V®𝜃(𝜔)必须对所有𝑥 ∈ D′都是𝐶0连续的。
(2) (边界一致性) ∀𝜔𝑏 ∈ 𝜕D和𝛿 ∈ R+，∃𝜖，使得∀𝜔 ∈ {𝜔，|𝜔 - 𝜔𝑏| < 𝜖}，|V®𝜃(𝜔) - 𝜕𝜃𝜔𝑏| < 𝛿。

连续性条件表明，变形场V®𝜃(x)必须是连续的。边界一致性条件表明，变形场必须在边界点处或接近边界点处紧密匹配边界点的变形。如果一个变形场V®𝜃(x)满足上述条件，给定边界导数𝜕𝜃x(𝑏)，我们就说它是有效的。
直观地，这些条件可以被看作是一个平滑边界插值问题：我们希望构造一个连续的场，同时在边界处匹配值。这些是至关重要的条件，并不总是能够满足的。在下面的小节中，我们将仔细确定一个满足这两个标准并且适合可微渲染的变形场V®𝜃(x)族。我们还将在第3.4节中展示与Loubet等人[2019]的重参数化方法的联系。他们的重参数化可以看作是构造一个通常不满足有效性标准的变形场，这解释了他们在结果中看到的偏差。

3.3 渲染积分的有效变形场

构造变形场V®𝜃(x)的平滑边界插值问题在渲染中提出了一个独特的挑战。在许多其他领域，如几何处理或数值计算，通常可以事先确定所有边界，然后离散化内部以构造平滑的场。然而，在基于区域的渲染公式中，我们希望从一开始就避免显式的不连续点枚举（如之前的工作[Li等人2018]中使用的边界采样）。
更具体地说，我们处理的是一个盲目插值问题，其中我们必须构造一个有效的变形场，而不需要在边界上有显式的样本。

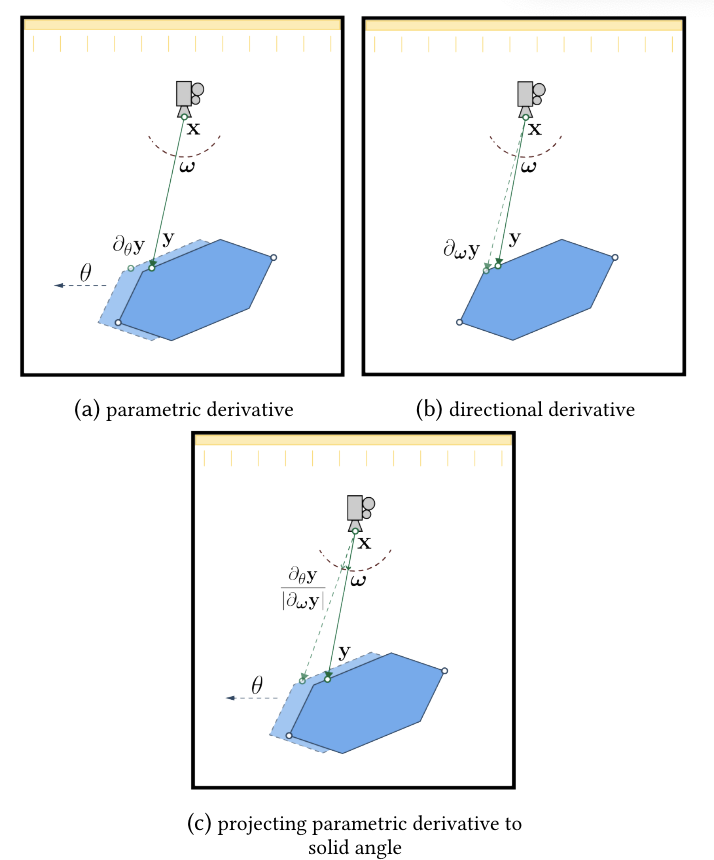
图5. 投影导数场。(a)和(b)说明了方向导数𝜕𝝎y和参数导数𝜕𝜃y之间的区别，因为它们是我们推导中的重要组成部分。(a)还显示参数导数在曲面y上的点处是连续的。©显示了在立体角空间Ω中一个点的参数导数的计算，该导数以相关场景点y的导数表示，我们很容易访问到这些导数。如图所示，使用变换𝝎→y的雅可比项来找到参数导数的投影版本。

利用场景结构。我们的方法利用了3D场景的流形结构，通过观察3D场景点𝜕𝜃x的导数对于所有表面点x ∈ X都是连续的。可见性项的不连续点仅在几何体被投影到被评估的辐射度的点的立体角空间X → Ω时出现。

选择变形场。我们希望为所有𝝎 ∈ Ω定义一个场V𝜃(𝝎)，使得第3.2节中的连续性和边界一致性条件得到满足。我们的策略是构造一个满足边界一致性但不一定要连续的场，通过微分射线-几何体交点过程实现。

渲染积分（方程1）通过射线-场景交点运算符将位置x处的立体角𝝎映射到场景点y，我们用y = Intersect(x, 𝝎; 𝜃)表示。具体而言，我们使用交点函数关于场景参数𝜃的导数作为我们的初始（无效）变形场，通过自动微分交点函数来获得y, 𝜕𝜃y, 𝜕𝝎y = Diff-Intersect(x, 𝝎; 𝜃)。具体来说，我们的变形场是：

V®(direct)𝜃(𝝎) = 𝜕𝜃y/|𝜕𝝎y|。（6）

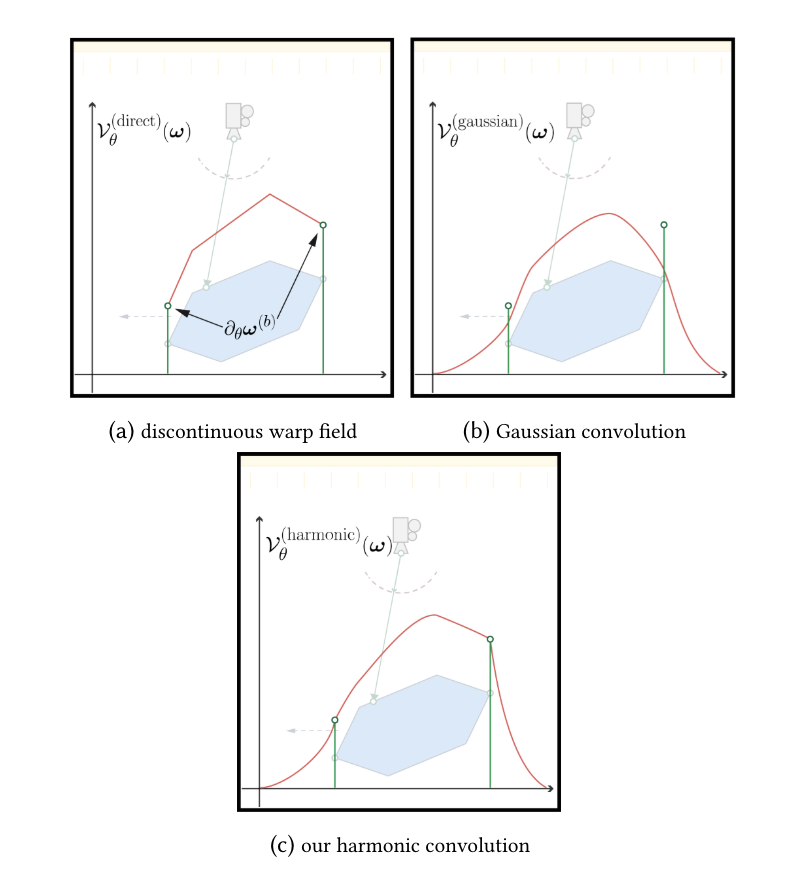
图6. 边界感知卷积。(a)使用射线-场景交点函数将域𝝎变换得到的变形形式。它在轮廓处不连续（用蓝色圆圈表示），但在边界处等于正确的导数（用绿色线表示）。(b)通过使用高斯核卷积变形场产生的变形场。这个场在任何地方都是连续和平滑的，但我们看到它在边界处不匹配真实的导数。更具体地说，在这种情况下，边界处的变形是边界两侧变形的平均值，其中只有一个代表边界处的变形。©我们提出的卷积方法使用反距离权重来强制场在边界处匹配真实的变形。得到的变形场在边界处既是连续的又是一致的。

除以雅可比|𝜕𝝎y|是为了将𝜕𝜃y的测度从面积测度转换为立体角测度。这个投影项与路径空间渲染方法[Veach 1998]中在立体角和面积公式之间转换的几何项相同。我们使用它来投影导数而不是辐射度。

变形场V®(direct)𝜃(𝝎)满足边界一致性标准，因为在接近边界的点处，导数𝜕𝜃y/|𝜕𝝎y|趋近于边界导数𝜕𝜃𝝎𝑏。

直观地说，这意味着给定点𝝎的移动速率等于对应3D点的移动速率，该速率由空间之间的投影雅可比进行调整（图5）。不幸的是，这个变形场是无效的，因为它破坏了连续性标准。例如，考虑两个角度，它们在边界的两侧非常接近，但它们与不同的表面相交，因此具有非常不同的变形。

变形场V®(direct)𝜃(𝝎)的不连续性也是为什么很难微分可见性函数的原因。通常情况下，对于可见性函数中的不连续点，只有一侧代表边缘。当我们尝试在不连续点的一侧评估变形时，相应3D点的移动与不连续点的移动完全无关。然而，为了创建一个连续的变形，我们必须以某种方式确保我们的变形场是连续的。

我们的解决方案是通过卷积直接变形场，使用确保边界一致性的权重。这修正了底层的不连续场V®(direct)𝜃(𝝎′)，产生一个平滑且连续的场V®(filtered)𝜃(𝝎;𝑤)：

V®(filtered)𝜃(𝝎;𝑤) = ∫Ω′ 𝑤(𝝎, 𝝎′)V®(direct)𝜃(𝝎′)d𝝎′/∫Ω′ 𝑤(𝝎, 𝝎′)d𝝎′。（7）

接下来，我们讨论如何选择权重𝑤，使得边界一致性得以保持。

边界感知卷积。权重应该是什么样的并不明显。作为一个反例，图6(b)展示了使用正态分布的权重得到的变形场。变形场严重偏离了边界处的真实变形，并且这个场仍然无效，因为它违反了边界一致性。边界附近一个点的变形将是两侧变形的平均值，这通常不等于（或甚至接近）边界处的变形。

我们的权重需要在接近边界的点处收敛到导数，以产生有效的插值。也就是说，当𝝎在边界上时，𝑤(𝝎, 𝝎′)应该趋近于无穷大，同时𝝎′趋近于𝝎。我们还希望当𝝎远离边界时，权重很小。我们从调和插值中获得灵感，通过选择使用到边界的反距离的权重。

不幸的是，我们不知道到最近边界点的真正距离，因为找到边界是困难的。相反，我们使用边界测试B(𝝎′)的概念，它作为边界的较弱定义。B(𝝎′)本质上是一个软指示函数，在边界处取值为零，在其他地方取非负值，即，𝝎′ ∈ 𝜕Ω =⇒ B(𝝎′) = 0。这是B(𝝎′)需要满足的唯一关键要求，这给了我们在它的形式上有很大的灵活性。附录A讨论了我们用于三角形网格的边界测试，而附录B讨论了边界测试的附加属性以及使用次优边界测试会发生什么。

现在我们可以写出我们的调和权重：

𝑤(harmonic)(𝝎, 𝝎′) = 1/(D(𝝎, 𝝎′) + B(𝝎′))。（8）

其中D(𝝎, 𝝎′)是𝝎和𝝎′之间的距离。对于我们的实现，我们使用von-Mises Fisher距离D(𝝎, 𝝎′) = e^{(𝜅(1-<𝝎,𝝎′>))}(-1)，但可以使用任何满足D(𝝎, 𝝎) = 0的平滑函数。

我们的权重满足有用的渐近属性，即当一个点𝝎(𝑏)趋近于边界（表示为𝜕Ω）时，𝑤(𝝎(𝑏), 𝝎)/∫Ω′ 𝑤(𝝎(𝑏), 𝝎′) = 𝛿(|𝝎(𝑏) - 𝝎|)，其中𝛿(.)是狄拉克δ函数。这意味着对于一个非常接近边界的点𝝎(𝒃)，权重是这样的，使得在𝝎(𝒃)处得到的变形等于直接变形。正如我们已经展示的，直接变形在边界处是一致的，这意味着使用调和权重的卷积也是一致的。图6©展示了我们调和插值的结果。

我们只分析边界附近的权重，而不是边界本身，因为我们的变形场只需要在平滑内部区域Ω - 𝜕Ω中定义。这允许我们的变形场在边界上的点处未定义，并且提出的调和权重在这样的点处是无限的。

像素预滤波。虽然原则上我们的方法可以处理不连续的像素预滤波，如盒式滤波，但我们总是选择连续的滤波。对于不连续的滤波，像素滤波积分∫𝐴 𝑓(𝝎)d𝝎在像素支持𝐴上需要考虑支持边界处的不连续点，以使散度定理成立。这意味着我们的边界测试𝐵(𝝎′)需要在这样的边界处返回0。为了简化边界测试的实现，我们总是使用高斯像素滤波，截断在4倍标准差的半径处，其中核的贡献与浮点误差无法区分。

3.4 与重参数化方法的关系[Loubet等人2019]

在我们转向解决调和卷积积分（方程7）的蒙特卡罗采样算法之前，我们讨论我们的方法与Loubet等人的重参数化之间的关系。

虽然我们以不同的方式推导出了边界项的区域形式，但Loubet等人通过旋转变换样本来消除积分的不连续点的方法实际上是我们公式的一个特例。我们将展示我们可以将他们的方法解释为应用一个特定的变形场，该变形场不满足边界一致性要求，从而给结果引入偏差。

重参数化方法应用了一个变换x = T(y; 𝜃)来尝试消除积分的不连续点：

I = ∫ 𝑓(x; 𝜃)dx = ∫ 𝑓(T(y; 𝜃); 𝜃)|𝜕yT(y; 𝜃)| dy。（9）

在附录C.1和C.2中，我们证明了这个变换可以使用关系式V𝜃(x) = [𝜕𝜽T(x; 𝜽)]𝜽=𝜽0转换为一个等价的变形场V𝜽(y)。其中𝜽0是我们想要计算导数的点。

给定一个变形场，我们也可以将其转换回一个变换，通过找到方程10右侧的解。

由于这是一个微分方程，存在许多可能性，取决于坐标系，T(x; 𝜃)的基本形式。附录C.2讨论了2D欧几里得和3D单位球坐标系中该方程的线性和旋转解。旋转解表示Loubet等人[2019]使用的变换的基本形式。
我们用R(𝝎; 𝜃)表示旋转解。这将可能的变换集限制为单位雅可比|𝜕𝝎R(𝝎; 𝜃)| = 1的变换，与𝜃无关。我们可以推断出这意味着相应的变形满足∇𝝎 . V𝜃(𝝎) = 0。不幸的是，这意味着简单的旋转重参数化并不总是有效的变形（图4显示了一种需要非零散度的场景示例）。

Loubet等人认识到这个缺点，并提出了一种更复杂的变换，该变换使用von-Mises Fisher分布（高斯的球面模拟）对附近的射线进行采样，并构造出这些旋转的平均值作为变换。这通常可以用R′(𝝎; 𝜃) = ∫ 𝑘(𝝎, 𝝎′)R(𝝎′; 𝜃)表示。由于变换和变形场是线性相关的，所以卷积变换的变形场V′𝜃(x) = [𝜕𝜃R′(𝝎; 𝜃)]𝜃=𝜃0与原始变换的变形场的卷积等价，即V′𝜃(x) = ∫ 𝑘(𝝎, 𝝎′)V𝜃(x)。这导致了类似于图6(b)所示的情况，其中得到的变换是平滑的，但未能满足边界一致性标准。

为了弥补这种偏差，Loubet等人[2019]在这种卷积之上引入了一种启发式方法。由于这种启发式涉及诸如排序和比较对象ID等离散操作，因此很难从分析上表达出得到的变形场及其性质。相反，我们转向第5节中呈现的地面真实情况的实证比较。

4 导数的蒙特卡罗估计

在前一节中，我们开发了区域采样的理论，并提出了变形场的公式。在本节中，我们开发了一个蒙特卡罗估计器，用于估计我们的散度区域积分（方程5）。在前一节中，我们提出了一个卷积变形场，它本身就是一个积分（方程7）。因此，我们构建了一个嵌套的蒙特卡罗估计器来估计导数积分。我们首先为外部散度积分生成样本𝝎，然后生成一组辅助样本{𝝎′1,…,𝝎′𝑁′}来估计内部卷积积分在𝝎处的值。图7总结了我们的渲染过程，以及一些像素内的可视化，以显示我们的中间阶段。

变形场的卷积积分包含一个用于归一化的除法。积分的倒数的朴素蒙特卡罗估计器不是无偏的，因为倒数不是线性操作（𝐸[1/𝑓] ≠ 1/𝐸[𝑓]）。幸运的是，使用俄罗斯轮盘反偏差方法[McLeish 2010]，可以从一个一致的估计器构造一个无偏的蒙特卡罗估计器。在本节中，我们提供了一个一致的估计器和一个无偏的估计器。
最后，调和卷积积分的朴素蒙特卡罗估计可能导致较大的方差。我们讨论了使用控制变量减少方差的技术。

4.1 估计变形场V𝜃(.)

我们的目标是估计散度区域积分（方程5），其被积函数为(∇𝜔 𝑓(𝜔; 𝜃)) · V®𝜃(𝜔) + (∇𝜔 · V®𝜃(𝜔)) 𝑓(𝜔; 𝜃)d𝜔。
对于外部散度积分的每个方向样本𝝎，我们采样𝑁′个辅助方向𝝎′𝑖，以估计变形场V®𝜃(𝝎)。回想一下，变形场是一个归一化的调和权重核的卷积（方程7和8）。虽然调和权重的分布取决于轮廓边缘的配置（图6），但它也与外部方向样本𝝎为中心的正态分布相关。因此，我们从外部方向样本周围的正态分布中进行重要性采样。
对于半球或球面采样，我们使用von Mises-Fisher分布。

这张图中的伪代码描述了一个蒙特卡洛估计器，用于计算光线在给定方向上的辐射度（radiance）的导数。这个估计器可能是用于渲染算法中的，特别是在光线追踪（ray tracing）中，用于计算场景中光线的微小变化对最终图像的影响。下面是伪代码的逐行解释：

1. function RADIANCE (x, @in)：定义了一个名为RADIANCE的函数，它接受一个点x和一个入射方向@in作为输入。
2. Sample outgoing radiance direction with incoming direction @in：从点x出发，沿着入射方向@in采样一个出射的辐射度方向。
3. y←INTERSECT(X, @)：计算从点x出发沿着方向@的光线与场景中物体的交点y。
4. L, agL, ogL←RADIANCE(y, @)：递归地调用RADIANCE函数，计算交点y处的辐射度L，以及在该点处的辐射度关于入射方向@的梯度agL和关于交点位置y的梯度ogL。
5. Ve(), Vw, Ve()←ESTIMATE-WARP(@, y, N')：使用ESTIMATE-WARP函数估计在点y处的入射方向@和出射方向N'之间的扭曲场Ve()，以及在该点处的入射方向Vw和出射方向Ve()。
6. SYI←(agL, Ve(w)) + LV.Ve(w)：计算辐射度L与出射方向Ve(w)的点积，加上辐射度L与出射方向Ve(w)的点积，得到一个中间结果SYI。
7. agI←agI + dgl：将辐射度L关于入射方向@的梯度agL累加到agI上。
8. I←fp(in, @)L：计算从点x出发沿着入射方向@in的辐射度I。
9. a wi I←a win(fp(in, @) L)：计算辐射度I关于入射方向@in的权重a wi。
10. return i, agI, oom I：返回辐射度I，关于入射方向@in的梯度agI，以及关于交点位置y的梯度ogI。
11. endfunction：函数结束。

这个伪代码可能是一个渲染算法的一部分，用于计算光线在场景中的传播和相互作用，以及这些相互作用如何影响最终的图像。特别是，它涉及到计算辐射度的导数，这对于优化渲染过程或进行某些类型的图像分析可能是有用的。

这份伪代码描述了一个名为ESTIMATE-WARP的函数，它用于估计扭曲场（warp field）的值。扭曲场在计算机图形学中用于描述光线在不同介质或表面之间的转换。这个函数可能是用于蒙特卡洛光线追踪算法中，以估计光线在场景中传播时的扭曲效应。下面是伪代码的逐行解释：

1. function ESTIMATE-WARP(， y， N)：定义了一个名为ESTIMATE-WARP的函数，它接受三个参数：一个点y，一个单位向量N（可能代表表面的法线），以及一个整数N，表示采样次数。
2. for i←(1…N') do：开始一个循环，循环N次，每次循环代表一次采样。
3. Sample w' from vMF distribution with mean：从具有均值的von Mises-Fisher（vMF）分布中采样一个单位向量w'。vMF分布是一种用于在单位球面上采样的概率分布，常用于表示方向或单位向量。
4. yf apy f， a wy； -DIFF-INTERSECT (x，)：计算从点y出发沿着w'方向的光线与场景中物体的交点f。-DIFF-INTERSECT可能是一个函数，用于计算光线与物体的交点，并考虑了光线的差异性（diffuse）反射。
5. B； ←BOUNDARY-DISTANCE (y)：计算点y到最近边界的距离B。这可能用于确定光线是否与场景的边界相交。
6. Wi← (exp (K-K(@，w；>)-1)+B 3； PDF( 1：计算权重Wi，它可能是基于光线与物体交点的距离和vMF分布的概率密度函数（PDF）来计算的。
7. 0wwi← awt exp( (K-K(，w>)-1)+Bi ) PDF(w) dey：计算加权的权重0wwi，这可能涉及到对权重进行归一化处理。
8. laoy； l：这行代码似乎不完整，可能是伪代码的错误或遗漏。
9. end for：结束循环。
10. z←Zwi：计算加权的平均值z，这可能是对所有采样点的某种度量的加权平均。
11. az←Z oww w wz v“：计算加权的平均值az，这可能是对所有采样点的另一种度量的加权平均。
12. Ve(w) <— 2(0wwi， V Y〉 Zw<Vw， ，az〉：计算扭曲场Ve(w)，这可能是基于加权的平均值和向量Vw的点积来计算的。
13. Vo.Ve(w)← Z2：计算扭曲场Ve(w)的平方，这可能是为了某种度量或归一化。
14. return Ve(w) ， Vw.Ve()：返回扭曲场Ve(w)和它的点积Vw.Ve()。
15. endfunction：函数结束。

算法1和2详细描述了计算存在不连续点的辐射度导数的嵌套蒙特卡罗估计器。由于调和卷积（方程7）中的积分除法，该估计器对于有限的𝑁′不是无偏的，但它是一个一致的估计（当𝑁′→∞时，它收敛到真实的导数）。
在实践中，我们发现即使在相当复杂的场景中，4到64之间的辅助射线计数也能提供非常稳健的导数估计。然而，由于权重𝑤(𝝎, 𝝎′)的归一化没有封闭形式的表达式，所以变形场的估计器不是无偏的。尽管如此，当𝑁′→∞时，它会收敛到真实情况，使其成为一致的。
去偏差我们的估计器。一般来说，使用俄罗斯轮盘[McLeish 2010]可以从一个一致的估计器产生一个无偏的蒙特卡罗估计器。这是一种在贝叶斯推断[Lyne等人2015]、核工程[Boot 2007]、机器学习[Beatson和Adams 2019]以及最近用于去偏差光子映射[Qin等人2015]和采样镜面光路[Zeltner等人2020]中常用的技术。

俄罗斯轮盘去偏差的直觉是取一个由一致的估计器产生的收敛序列𝑇0,𝑇1,𝑇2,…，并构造以下无穷级数：

𝑇ˆ = 𝑇0 + Σ∞𝑖=1 (𝑇𝑖 −𝑇𝑖−1)。（11）

由于𝑇ˆ收敛到正确的答案，如果我们可以为𝑇ˆ构建一个无偏的估计器，我们就可以将一致的估计器变成一个无偏的。为无穷级数构建无偏估计器是物理基础渲染中的一个常见任务：在路径追踪中，通过概率性地终止估计，可以估计间接反弹的无穷诺依曼级数。

使用同样的想法，我们通过从一个离散分布中采样一个有限的长度来采样级数𝑇ˆ。我们将N′视为一个服从几何分布的随机变量。对于每个路径反弹，在辅助采样步骤中，我们为变形场的估计采样一个新的N′。这个版本产生一个无偏的变形场估计，反过来使我们的导数估计无偏。

算法3描述了蒙特卡罗估计器。

在实践中，使用具有较高N′的一致版本来减少偏差通常比俄罗斯轮盘快，因为管理动态数量的射线可能会很复杂，尤其是随着渲染基础设施继续转向内存受限的GPU。

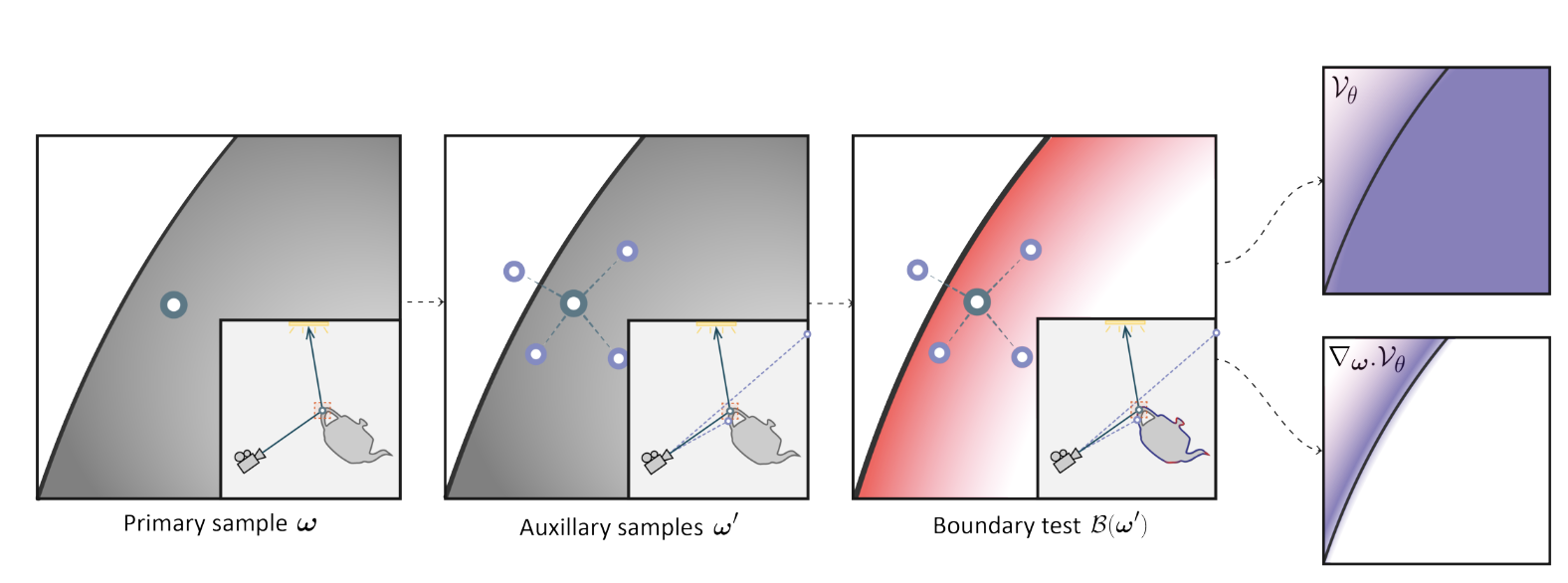
图7. 我们的算法首先根据简单的路径追踪来采样射线𝝎。为了计算导数的边界贡献，我们需要在这一点上估计变形函数。为了实现这一点，我们的方法使用von-Mises Fisher分布围绕这个样本𝝎采样一定数量的辅助射线N′。然后，我们根据表面法线（如附录A所述）在每个辅助样本处计算边界测试B(𝝎′)。这些边界值进一步使用方程8进行处理，以产生样本的权重。最后一步计算辅助样本处的直接变形V(direct)𝜃的加权平均值，以产生主样本处的变形场及其散度的估计。

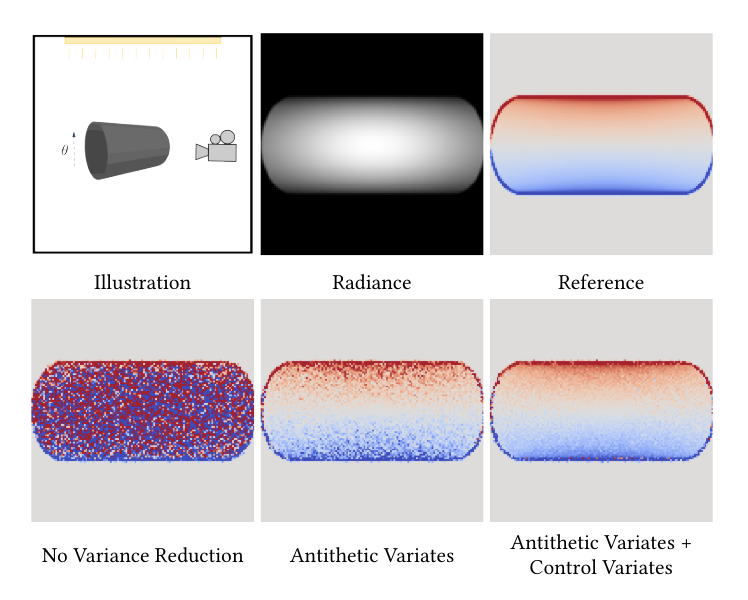
图8. 方差减少。我们使用反向变量和控制变量来对抗卷积核引入的内部区域的额外方差。我们展示了反向变量的方差减少，其中我们在核中心的两侧均匀采样。通过使用线性假设构建的近似估计器来控制估计器，我们进一步减少了方差。

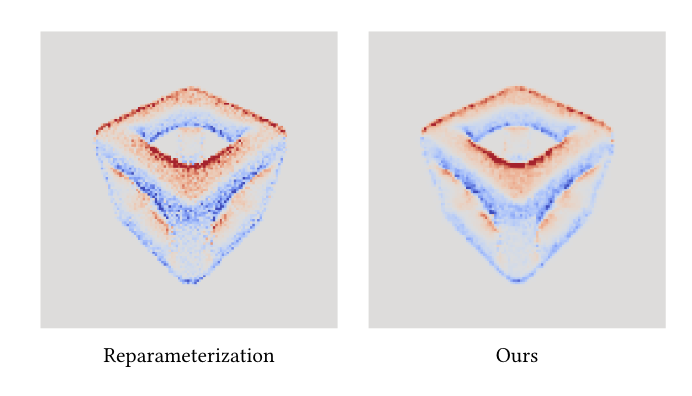
图9. 我们比较了我们的方法和重参数化方法[Loubet等人2019]的梯度方差。比较使用了两种方法的每个像素的相等路径数。由于Loubet等人的方法为每个样本追踪两条相关的路径，我们将我们的每个像素32个样本的渲染与他们的每个像素16个样本的渲染进行比较，同时保持相同的辅助射线数（每个反弹4个）。

4.2 方差减少

如果直接使用而不进行显式的方差减少，我们估计器的某些部分会表现出高方差。我们发现平滑区域受到调和权重和变形场散度的方差影响很大。
为了说明方差问题，考虑一个具有无限、平坦发射器的场景，其中参数𝜃是发射器的平移。如果这个发射器也完全垂直于我们的观察方向（面向摄像机），那么我们的预期梯度为0，因为所有点相对于𝜃以完全相同的速度移动。然而，我们发现权重归一化的梯度表现出非常高的方差，因为每个单独的空间权重导数∇𝝎𝑤(𝝎, 𝝎′)可能具有很大的值，这取决于样本相对于分布中心的位置。尽管场景中没有复杂性，预期梯度为0，但得到的估计器表现出高方差。
反向变量。我们解决这个问题的方法是应用反向变量[Owen 2013]。这种广泛使用的方差减少技术的关键思想是将样本进行变换，使得得到的估计器与原始估计器负相关。对于对称权重，如高斯分布和von-Mises Fisher分布，找到这样的变换相当简单。我们围绕分布中心旋转180度。直观地说，由这个变换样本的权重引起的梯度贡献恰好是原始样本贡献的负值。图8展示了使用反向变量获得的显著方差减少。
控制变量。当底层变形场大致均匀时，反向变量提供了最大的方差减少。考虑与之前相同的场景，但有一个与摄像机成一定角度的平坦发射器。我们的交点导数𝜕𝜃𝜔不再是均匀的，而是表现出近似线性变化。我们发现，尽管我们的边界导数估计器的预期值为0（因为没有边缘，所有贡献都来自内部导数积分），但它表现出高方差，因此需要大量样本才能收敛到正确值。然而，我们看到在这种特定情况下，如果我们知道底层线性表面的斜率，我们可以直接计算变形的散度，而不需要经过广泛的估计步骤。
因此，我们使用这个近似估计器作为控制变量来减少无偏估计器的方差。附录D提供了线性近似构造和其在方差减少中的实用性的更多细节。图9比较了相对方差（具有反向变量和控制变量）和重参数化方法。这里概述的方差减少方法在用于优化时特别重要（图11和12），因为我们通常使用非常低的样本数以实现快速收敛。

5 结果和讨论

我们在开源redner存储库[Li等人2018]2中实现了我们方法的一致和无偏版本，主要是因为它已经包含了获取参数和空间导数（𝜕𝜃𝐿, 𝜕𝝎𝐿）的基础架构。我们的实现在多核CPU上运行，并使用Embree[Wald等人2014]进行射线追踪。

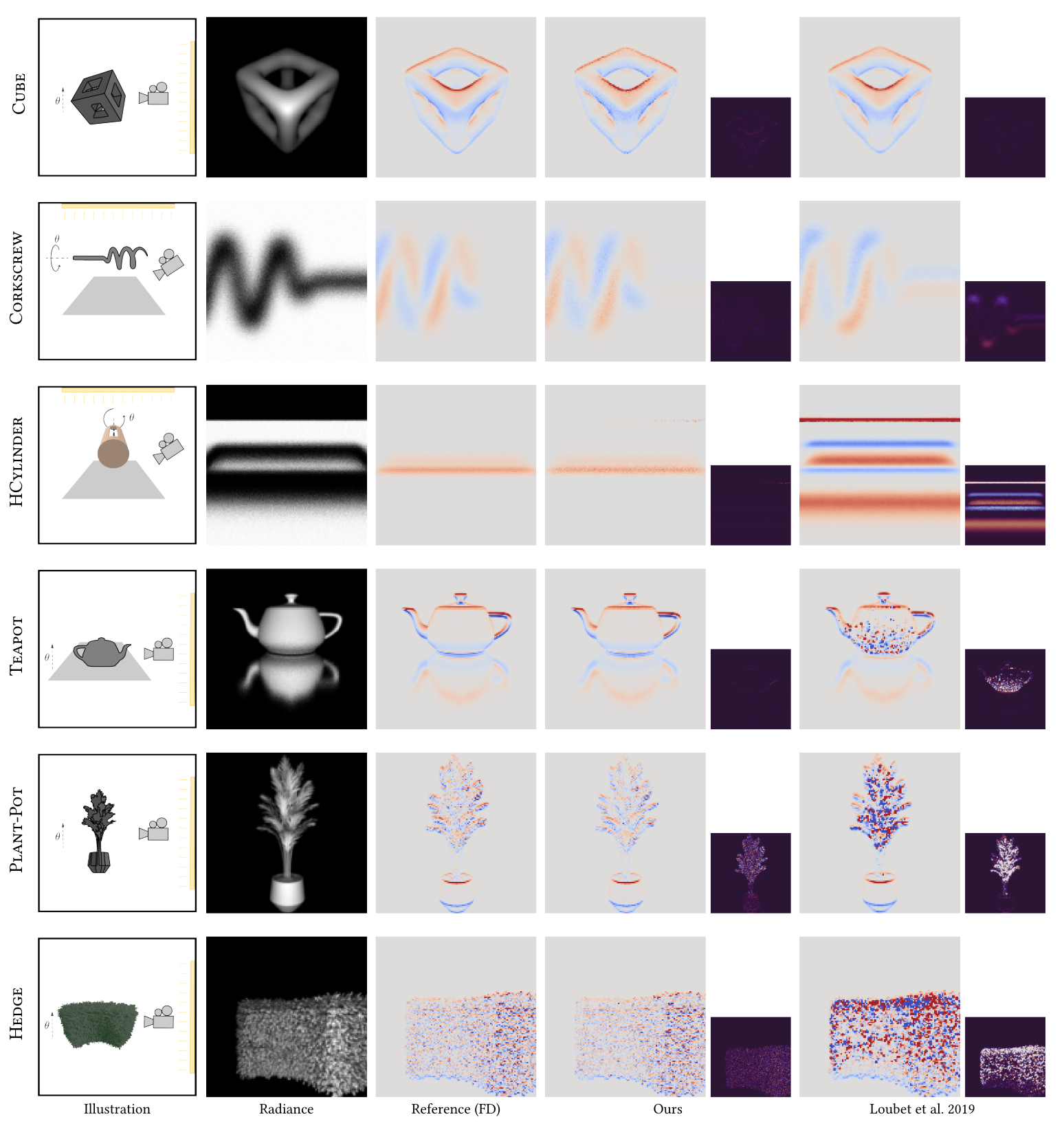
图10. 我们在具有不同复杂度级别的场景上比较了我们每像素梯度与重参数化方法[Loubet等人2019]。立方体具有简单平滑的几何形状和运动，以显示我们的区域采样方法为直接可见性产生了正确的边缘导数。开瓶器和HCylinder展示了旋转的类似圆柱体的网格，这为区域采样方法创造了困难的情况。茶壶展示了我们的方法即使在尖锐的镜面反射下也是准确的。Plant-Pot和Hedge使用具有大量基本体的网格来产生复杂的像素内边缘配置。立方体、HCylinder和茶壶使用了von-Mises Fisher方向光，而其他使用了矩形区域光。插图可视化了有限差分参考和产生的梯度之间的绝对误差。我们的方法在所有情况下都非常接近参考。这些实验旨在突出每种方法的偏差，因此它们在每像素高样本数（≥128）下进行了比较。

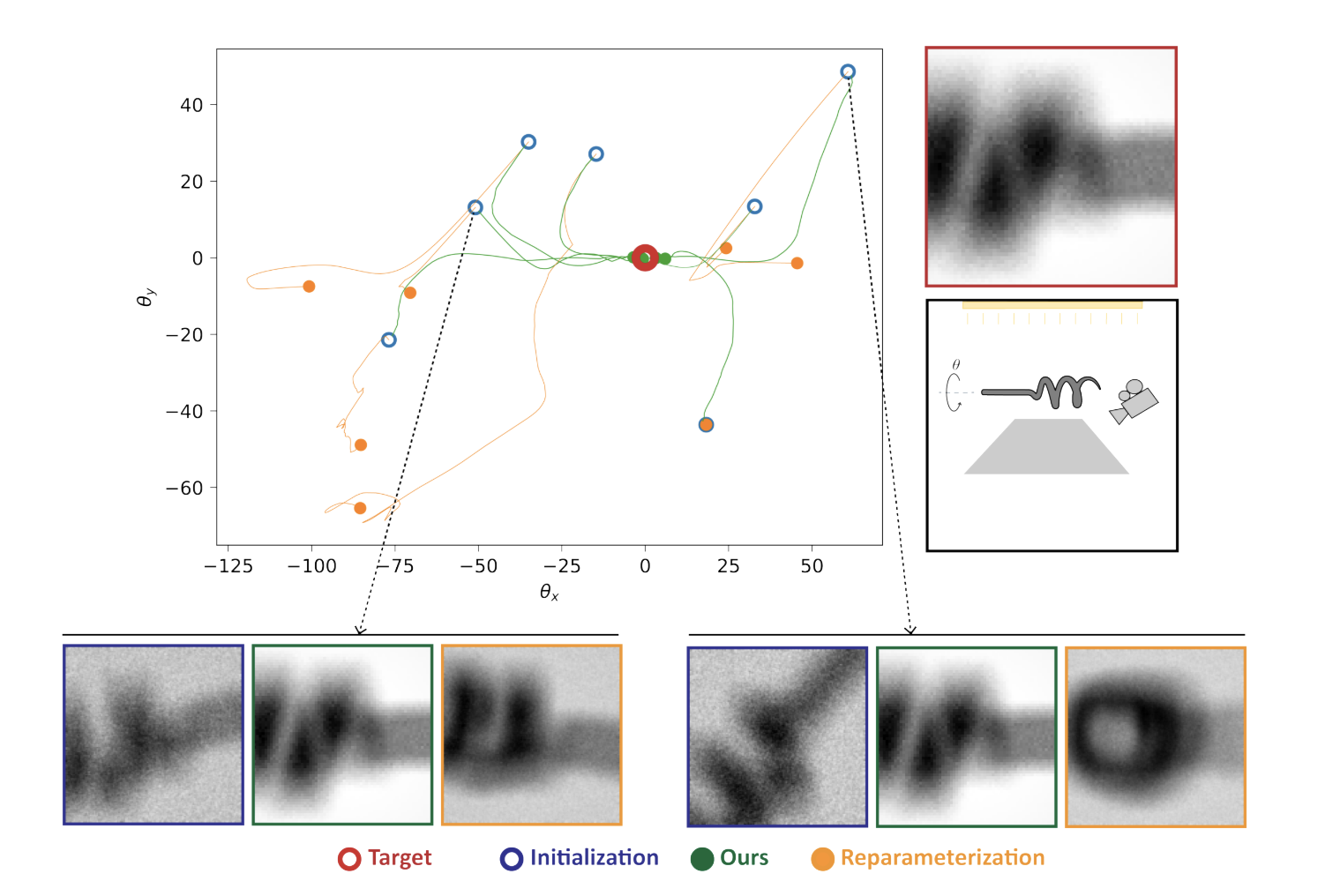
图11. Optim-Corkscrew：我们在基于梯度的优化任务上比较了我们的方法和重参数化方法[Loubet等人2019]。两种方法都被要求通过观察其柔和阴影来恢复开瓶器的角向方向，从相同的初始化集（蓝色圆圈）开始。由于重参数化方法中的偏差，没有优化收敛（橙色点）。相比之下，我们能够从所有初始化中恢复目标解。根据Loubet等人的建议，对于重参数化，我们使用了一个平滑区域光源，旨在在边界附近具有平滑衰减，以减少偏差。平滑衰减导致场景亮度变化。

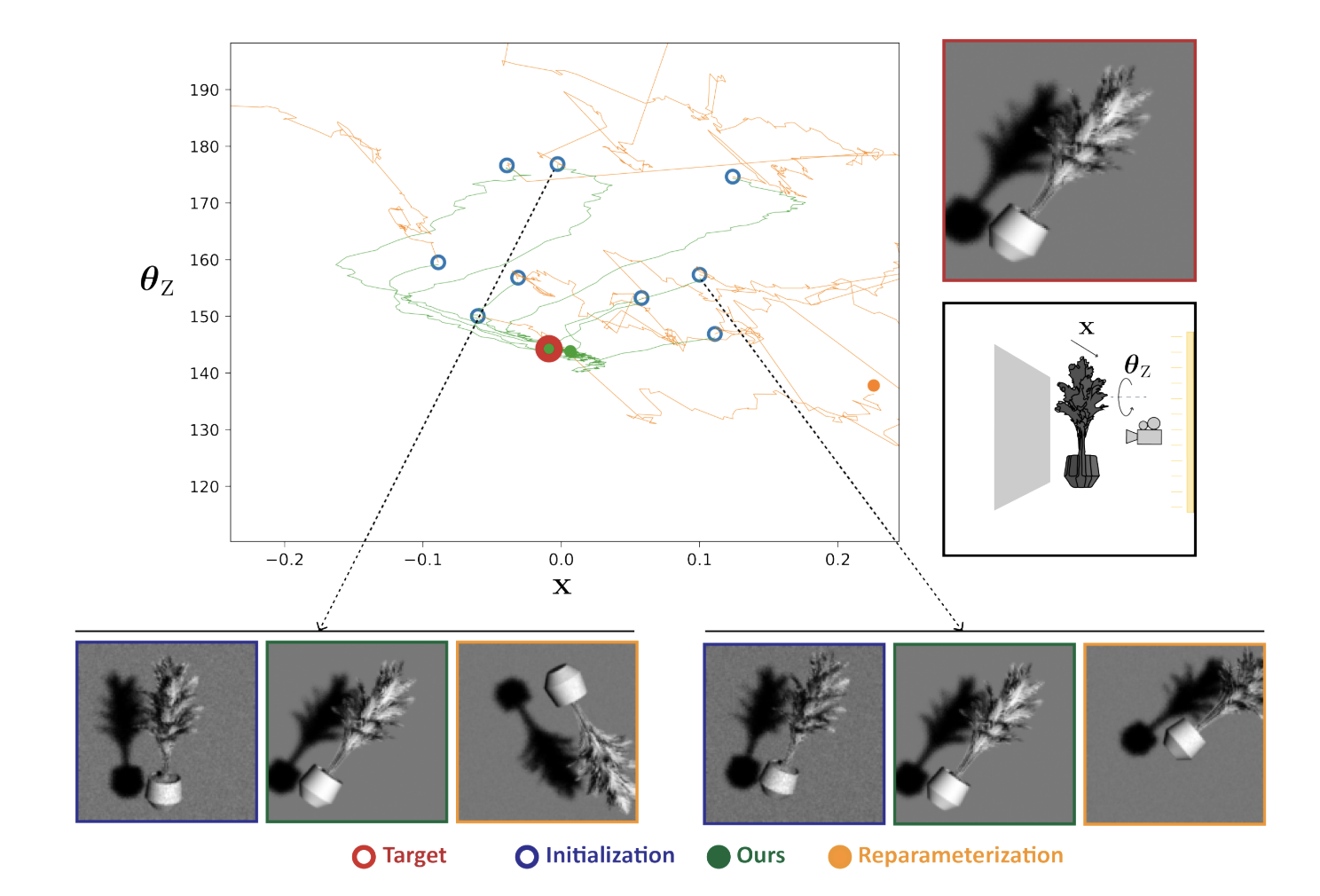
图12. Optim-Plant：我们在每像素8个样本的情况下，对一个具有复杂结构的物体进行了6自由度姿态优化实验。我们的估计器提供了稳健的梯度，即使在低样本数下也能实现平滑收敛。重参数化梯度方法采用了特定的启发式方法来更好地估计正确的梯度。然而，它设计时假设一个像素包含一个简单的不连续点配置，这个假设在这里失效，导致优化完全发散。我们可视化了多个初始化的轨迹。

5.1 与Loubet等人[2019]的比较

我们将我们的方法与Loubet等人的重参数化方法[2019]进行比较。他们的方法依赖于通过近似局部旋转来计算导数的近似值。由于他们的方法可以被解释为构造一个在边界处不一致的变形场，所以底层偏差与不连续点处变形的总差异成正比（第3.4节和图4）。为了减少偏差，Loubet等人引入了一个核卷积（类似于我们在方程（8）中的调和卷积）以及一个基于邻域采样调整变形估计的启发式方法。尽管这些调整显著减少了简单边界配置下的偏差，但它：
• 对于具有密集和交错几何体的场景（如密集灌木丛或植物）失败；
• 当内部运动与边界不一致时引入偏差；
• 不容易泛化（更多讨论见第5.4节）。
在图10中，我们包含了一个比较单个参数的每像素梯度的比较，以突出重参数化方法的近似引入的系统偏差。
为了展示我们健壮、一致（或无偏）梯度的重要性，我们使用大量初始化探索了两个复杂的姿态估计问题，即Optim-Corkscrew（图11）和Optim-Plant（图12）。我们展示了偏差的重参数化方法始终无法获得正确解。在某些情况下，由于启发式引入的偏差，该方法甚至完全发散。
Optim-Corkscrew和Optim-Plant都使用了128×128的目标分辨率、三级图像金字塔损失和一个矩形区域光光源。对于重参数化方法，我们使用了Loubet等人[2019]推荐的平滑区域发射器，它模糊了矩形光光源的外10％以减少偏差。Optim-Corkscrew使用了𝑁 = 8个样本每个像素和𝑁′ = 8个辅助样本，而Optim-Plant使用了𝑁 = 16个样本每个像素和𝑁′ = 4个辅助样本。两个优化都使用了固定的𝑁′变体（一致变形估计器）。俄罗斯轮盘变体在最终结果中没有提供显著差异。Optim-Corkscrew使用𝜅 = 5 × 105作为其权重分布，而Optim-Plant使用𝜅 = 104。手动调整的集中参数𝜅 = 104对我们的所有实验都非常有效，提供了几乎零偏差，除了旋转开瓶器的情况，这对于基于区域的方法来说是一个困难的挑战。这种情况需要更集中的von-Mises Fisher分布以避免在𝑁′固定时出现偏差。我们将选择集中参数的自适应方法作为未来的工作。

5.2 与Li等人[2018]的比较

我们还将比较我们算法与Li等人[2018]提出的无偏边缘采样方法的方差和性能。边缘采样是一种边界方法，旨在找到轮廓边缘并采样它们上的点来估计边界积分。我们在图13中的实验表明，虽然这对于第一次反弹（直接可见性）非常有效，但它很难找到高阶效应（如光泽反射）的轮廓。对于具有高深度复杂度的场景，这种效果会更糟，如图1和图13中的Hedge场景所示，它包含超过20万个三角形排列在密集层中。由于轮廓采样不考虑遮挡，大多数采样到的边界点最终被遮挡。这导致几乎完全错过了光泽反射，表现为噪点而不是反射。边缘采样仍然是无偏的，但由于采样较差，可能需要很长时间才能收敛（当尝试使用简单的路径追踪器渲染焦散时也会出现类似的现象）。相比之下，我们的方法是基于区域的，不受这些采样问题的影响，尽管这以增加内部的方差为代价。

5.3 性能

尽管是CPU绑定的，但我们的方法具有合理的运行时间。对于实际优化实验Optim-Corkscrew和Optim-Plant（图11和图12），我们的CPU实现方法分别需要0.95秒和4.88秒进行一次完整的迭代。基于GPU的重参数化方法每次迭代需要0.28秒和0.35秒。对于我们的方法，我们在Intel Core i9-9900K上运行。对于Loubet等人的方法[2019]，我们使用他们的仅限GPU实现在使用OptiX的11GB NVIDIA RTX 2080 Ti GPU上运行。
图14显示我们的方法在与redner的CPU实现[Li等人2018]进行比较时具有相似或更好的性能。Loubet等人[2019]表明他们与redner的性能相似（在GPU上）。因此，如果我们的方法移植到GPU上，我们期望获得类似的性能提升，约为5倍。对于更简单的几何体，边缘采样更快，其中我们的一致方法的运行时间在2倍以内。然而，随着场景复杂度的增加，这个差距迅速缩小，对于包含超过20万个基本体的Hedge场景来说，我们的一致方法比边缘采样更快。
图14还展示了我们的无偏俄罗斯轮盘变体（算法3中描述）的性能。尽管对于我们的一致性和无偏性方法来说，辅助射线的平均数量是相同的，但由于俄罗斯轮盘技术所需的额外簿记开销，这使得这个变体慢了两倍。这是我们主要在优化实验中使用我们的一致性方法的一个原因。

5.4 泛化性的讨论

与在存在不连续性的情况下进行微分的其他方法不同，我们的方法已经从一个一般的积分中推导出来。它仅依赖于边界测试B(.)，对于不同的积分问题可以快速重新定义。一般来说，边界测试比实际边界本身更容易计算。这打开了令人兴奋的可能性范围。
扩展到其他表示法。为了定义一个易于计算的边界测试，我们注意到当前使用的三角形网格比许多其他表示法（如符号距离场、贝塞尔曲线、隐式函数以及大多数曲线几何体（球体、圆柱体等））更难处理，因为信息局部性更强。因此，原则上我们的方法是可以用于其他几何表示法的，只需修改边界测试即可。大多数现有方法假设由平面元素组成的网格结构，不清楚如何将它们扩展到新的表示法。
扩展到分布效果。我们估计算法的核心思想推导基于散度定理，该定理可以推广到更高维空间。因此，我们的变形方法可以直接应用于对其他渲染域（如运动模糊（3维空间，两个空间和一个时间坐标）和景深（4维空间，两个空间和两个角变量））进行微分。边界测试将需要相应地重新定义以测试更高维空间中的边界。
扩展到路径空间。我们的想法也可以潜在地应用于更复杂的域，如路径空间[Zhang等人2020]和原点样本空间。然而，首先必须调查路径空间中边界的定义，因为路径空间中的一个单独点可以穿过几个遮挡物。目前还不清楚哪种定义将在路径空间中产生有效的变形场。

5.5 局限性

隐式边缘。我们当前的边界测试B(.)实现没有自动考虑三角形网格中的隐式边缘（三角形自交）。这其中的含义是微妙的：由于样本没有被正确加权，隐式边界点的变形被估计为邻域中变形的平均值。这个有偏差的估计通常仍然非常准确，并且产生的结果类似于重参数化技术。然而，由于我们的边界测试B(.)没有检测到隐式边缘，得到的变形场没有有效性的保证，因此我们的方法在存在这种隐式边缘的情况下不能证明是无偏的。
实际实现中的截断偏差。在实践中，类似于通过俄罗斯轮盘进行去偏差的其他方法（如路径追踪），我们的方法必须在某些有限的限制下截断，否则会耗尽时间和计算内存。我们选择的限制（𝑁′ ≤ 512）足够大，使得由此产生的截断偏差与浮点数误差无法区分。然而，根据核大小和内存限制的选择，我们可能会遇到估计器产生不可忽略偏差的情况。
我们可以通过切诺夫-霍夫丁定理来合理地解释这种行为，该定理可以用来找到我们内部变形场估计器的渐近衰减率。通过俄罗斯轮盘修改得到的方差和截断偏差可以大致与这个衰减率联系起来。关于一般蒙特卡罗估计器的这种分析的一个例子可以在McLeish的文章[2010]中找到。
俄罗斯轮盘去偏差的不连贯工作负载。我们的俄罗斯轮盘去偏差可能会为并行执行引入不连贯的工作负载。每个路径顶点可以具有不同的辅助射线追踪数量，导致线程发散和动态内存分配。我们将高效的GPU实现作为未来工作。

6 结论

我们已经使用散度定理将边界采样和区域采样方法统一到了可微渲染中。我们进一步陈述了区域采样估计器要一致/无偏的条件：变形场的连续性和匹配边界速度。我们展示了为什么现有的区域采样方法不会产生无偏导数。这使我们能够开发一种算法，该算法通过使用受调和插值启发的权重应用额外的卷积来构建一致或无偏导数的估计器。我们的方法具有区域采样的简单性优势，因为变形场可以在标准蒙特卡罗渲染过程中计算，并且具有无偏的优势。我们已经通过反向渲染实验证明了梯度的无偏估计器对于稳定收敛至关重要。此外，像我们这样的区域采样反向传播方法是通用的。它们可以依赖于为前向传递开发的采样基础架构，并自然地处理深度和几何复杂性。

https://dl.acm.org/doi/pdf/10.1145/3414685.3417833

附件

A 边界测试 B(.)

我们利用第3.3节中定义的宽松要求实现了边界测试函数B(.)。主要要求是当𝝎接近边界时，B(𝝎) → 0。如图15所示，我们可以利用表面法线来设计一个好的边界测试。在轮廓点处，表面法线和射线方向的点积为0，并且在边界内是连续函数（B(𝝎)不需要在边界上连续）。由于可以快速计算各种表示的这个点积，因此它为计算B(𝝎)提供了一个轻量级的起点。对于三角形网格，我们需要处理仅与一个面相关的开放边。我们通过在每个顶点处将点积应用于非线性函数来额外控制扩散。

我们使用以下过程计算三角形网格的边界测试B(.)：
(1) 我们找到在方向𝝎上与射线相交的三角形。对于每个三角形顶点，检查是否存在任何相邻边是轮廓边。如果一个边（i）有一个相邻面是背面的，或者（ii）它是开放的（只有一个相邻面），那么它就是轮廓边。
(2) 对于每个顶点𝑣，计算一个值B𝑣。如果一个顶点𝑣与一个轮廓边相关联，则设置B𝑣 = 0。对于没有轮廓边的顶点，我们计算非线性组合（a）（b）

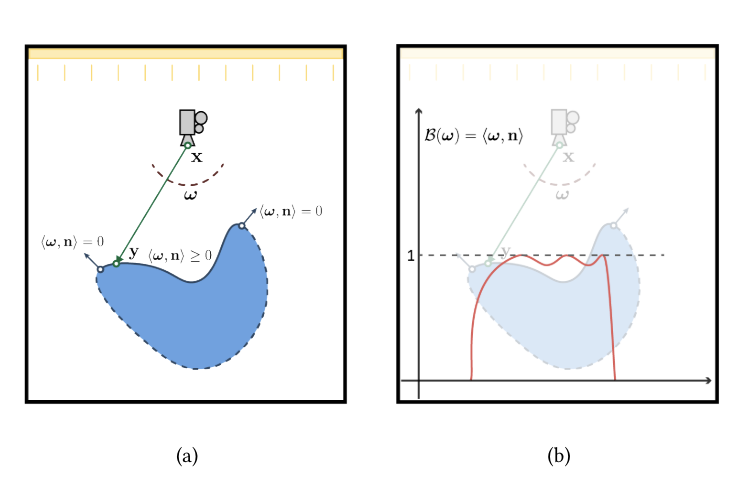
图15. (a) 复杂平滑曲面的插图。我们注意到所有对摄像机可见的点都是这样的，即摄像机方向和法线方向的内积⟨𝝎, n⟩为正。在轮廓处，这个内积为0。(b)显示了曲面上点积的变化，展示了在内部（不包括边界点），这是一个平滑函数。
⟨𝝎, n⟩的点积，B𝑣 = 1−(1−⟨𝝎,n⟩²⁾(1−(1−𝛽))。这里，n是每个顶点的法线，预先计算为所有相邻面的法线平均值。参数𝛽控制扩散速率，我们在实验中使用𝛽 = 0.01。我们经验性地发现这个值给了我们最小的方差，并且对场景组成或几何形状不敏感。
(3) 我们使用重心坐标将顶点处的B(.)传播到交点处。
然而，对于一些过度细分的低几何细节对象，构成边界的网格元素可能会变得非常小，导致得到的边界函数非常稀疏，导致估计器噪声很大。通过在网格上传播信息，可以设计出行为更好的边界测试，尽管这会增加复杂性。

B 变形函数的连续性

在第3.3节中，我们基于调和插值（方程8）定义了一组权重。调和权重直接依赖于边界测试函数B(.)。在这里，我们讨论一些B(.)的其他属性。

我们可以从其散度来推理变形场V𝜃的连续性。如果对于内部（非边界）点散度是有限的，那么它必须遵循变形场在内部是连续的。使用典型的向量微积分恒等式和微分乘积规则，我们将V𝜃的散度表示为
∇𝝎 . V𝜃(𝝎) = ∫Ω 𝜕𝝎𝑤(𝝎, 𝝎′) 𝑇 V(𝑑)𝜃(𝝎′) ∫Ω 𝑤(𝝎, 𝝎′)d𝝎′ - 𝑤(𝝎, 𝝎′)V(𝑑)𝜃(𝝎′) 𝑇 ∫Ω 𝜕𝝎𝑤(𝝎, 𝝎′)d𝝎′ (12)。
这个散度方程除了是我们算法的重要量外，还只依赖于相对于主样本𝝎的权重的导数。只要这个导数在所有内部点都存在，散度就是有限的。很容易看出，只要我们的距离函数D(𝜔, 𝜔′)是可微的，我们提出的方程8中的调和权重就满足这个性质。这意味着B(.)不需要可微或甚至连续，以使得到的变形场连续。

C 与重参数化的关系

扩展第3.4节的讨论，我们证明了一个变形场V𝜃(x)可以转换为一个重参数化x = T(y; 𝜃)，反之亦然。在整个证明过程中，我们假设我们试图在参数空间中的一个已知点处找到关于𝜃的导数，我们将这个点表示为𝜃0。
C.1 T(x; 𝜃) → V𝜃(x)
对于一个给定的重参数化T(y; 𝜃)，得到的积分可以重写为
I = ∫ 𝑓(x)dx = ∫ 𝑓(T(y; 𝜃); 𝜃)|det𝐽T|dy
其中𝐽T是重参数化的雅可比矩阵。
那么在𝜃 = 𝜃0处得到的参数导数就是
𝜕𝜃I = ∫ h 𝜕𝜃𝑓(T(y; 𝜃); 𝜃)|det𝐽T| i 𝜃=𝜃0 dy + ∫ h 𝑓(T(y; 𝜃); 𝜃)𝜕𝜃|det𝐽T| i 𝜃=𝜃0 dy
我们使用两个性质来得到导数的最终形式：
(1) 通过构造，变换T(y; 𝜃)遵循规则
𝜃 = 𝜃0, T(y; 𝜃0) = y [Loubet等人2019]
(2) 雅可比公式[Magnus和Neudecker 1999]，它指出
𝜕𝜃|det𝐽T| = tr(adj(𝐽T)𝜕𝜃𝐽T)
第一个性质还暗示了雅可比矩阵在𝜃 = 𝜃0时的伴随矩阵是单位矩阵I。我们还注意到雅可比矩阵的迹仅仅是底层映射的散度。
应用这些观察结果，我们得到以下方程：
[𝜕𝜃I]𝜃=𝜃0 = ∫ 𝜕𝜃𝑓(y; 𝜃0)dy + ∫ 𝜕y𝑓(y; 𝜃0)[𝜕𝜃T(y; 𝜃)]𝜃=𝜃0 dy + ∫ 𝑓(y; 𝜃0)∇y.[𝜕𝜃T(y; 𝜃)]𝜃=𝜃0 dy
这个方程现在与方程5的形式相同，这意味着使用变形场V𝜃(x) = [𝜕𝜃T(x; 𝜃)]𝜃=𝜃0会产生一个等价的积分。
C.2 V𝜃(x) → T(x; 𝜃)
要从一个变形场转换回一个变换，我们找到微分方程V𝜃(x) = [𝜕𝜃T(x; 𝜃)]𝜃=𝜃0的解。存在几种可能性来产生相同的变形场的变换。在这里，我们详细介绍两种不同坐标系下最简单的变形场。
2D自由坐标。考虑变换
T(y; 𝜃) = y + (𝜃 - 𝜃0)V𝜃(x) (13)
这满足了附录C.1中的属性1，即∇yT(y; 𝜃) = I。
还要注意的是[∇yT(y; 𝜃)]∇y=V∇y。
现在可以将附录C.1中的结果应用于这个变换，这表明使用我们的变形场积分与给定的变形场V∇y等价的重参数化积分。
3D单位球坐标。以类似的方式，我们可以为约束在单位球上的坐标找到一个简单的变换。一个简单的平移在这里是错误的，因为它会将点变换到球面域之外。相反，变换将不得不是一个旋转。
R(θ; 𝜃) = cos (θ - θ0) * |V∇θ| + sin (θ - θ0) * |V∇θ| * V̂∇θ

D 控制估计器

在本节中，我们详细讨论第4.2节的内容。具体来说，我们提供了一种明确的线性近似形式，通过控制变量法来减少主估计器的方差。

我们重新审视变形区域边界积分（方程5），以理解方差的来源：

I𝐵 = ∬D′ (∇x𝑓(x; 𝜃)) · V®𝜃(x)dx + ∬D′ (∇x · V®𝜃(x)) 𝑓(x; 𝜃)dx

我们使用像素预滤波积分来说明我们控制变量的应用。我们控制变量也适用于次级反弹。

当计算整个图像的导数时，每个像素都是有效辐射度𝑓(x; 𝜃)的积分，它是响应函数（预滤波𝑘(x)）和入射辐射度函数（𝑔(x; 𝜃)）的乘积。在我们所有的实验中，预滤波是一个标准正态分布，标准差为𝜎 = 1/2px。这里，x是2D图像平面上的坐标。

为了清晰起见，我们将使用随机变量和期望来表达我们的积分。我们还将使用线性代数符号。

现在可以将边界积分公式中的第一项写成像素域上的二维均匀随机变量x的函数（假设x = 0®是像素中心）。

I(1)𝐵 = Ex (𝑔(x; 𝜃)𝜕x𝑘(x) · V®𝜃(x)) + Ex (𝑘(x)𝜕x𝑔(x; 𝜃) · V®𝜃(x))

方差的主要来源是展开式的第一项，𝑀 = 𝑔(x; 𝜃)𝜕x𝑘(x) · V®𝜃(x)。项𝜕x𝑘(x)只是正态分布的导数，其期望值为0。然而，一般来说，这个项在像素域上是非零的。虽然我们知道𝜕x𝑘(x)的期望值，但乘积V®𝜃(x)𝑔(x; 𝜃)𝜕x𝑘(x)的均值是未知的。

为了解决这个问题，我们通过找到一个线性近似𝑔 ∗ V，使得得到的估计器具有已知（即分析可计算）的均值来构造一个近似估计器。

可以使用𝑔(.)（𝜇𝑔 = Ex [𝑔], ∇𝑔 = Ex [𝜕x𝑔]）和V(.)（𝜇V = Ex [V], ∇V = Ex [𝜕xV]）的均值和一阶导数的均值来构造一个局部线性近似。幸运的是，由于在计算主估计时可以访问辐射度𝑔(.)的导数以及变形场V(.)，因此估计这些量是容易的。

然后，近似的一阶导数就是矩阵𝐴 = 𝜇𝑔∇V + 𝜇V ∇𝑇𝑔。我们控制变量然后是（在二次形式下）

C = 𝜕x𝑘𝑇𝐴x (14)

由于𝑔(.)是一个标量，V(.)是一个向量，这些量的一阶导数分别是一个向量和一个矩阵。剩余的随机变量𝑘(x)和x具有已知的分布。

因此，可以通过使用一些常见的统计结果，特别是二次形式的期望值来计算期望值：

E[C] = tr(𝐴 cov(𝜕x𝑘𝑇, x)) + E[𝜕x𝑘]𝑇𝐴 E[x]

对于正态分布的情况，这简化为

E[C] = 𝜎^2 tr(𝐴)

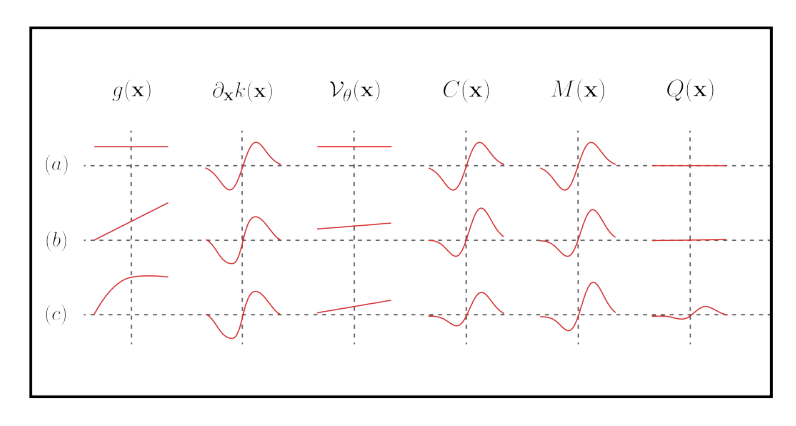
图16说明了通常情况下，C与M相关，因此得到的估计器Q = M - C + E[C]具有减少的方差。

这篇关于无偏扭曲区域采样在可微分渲染中的应用的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---