本文主要是介绍吴恩达深度学习笔记:深度学习的 实践层面 (Practical aspects of Deep Learning)1.13-1.14,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
- 第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
- 1.13 梯度检验(Gradient checking)
第二门课: 改善深层神经网络:超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)
第一周:深度学习的 实践层面 (Practical aspects of Deep Learning)
1.13 梯度检验(Gradient checking)
梯度检验帮我们节省了很多时间,也多次帮我发现 backprop 实施过程中的 bug,接下来,我们看看如何利用它来调试或检验 backprop 的实施是否正确。
假设你的网络中含有下列参数, W [ 1 ] W^{[1]} W[1]和 b [ 1 ] b^{[1]} b[1]…… W [ l ] W^{[l]} W[l]和 b [ l ] b^{[l]} b[l],为了执行梯度检验,首先要做的就是,把所有参数转换成一个巨大的向量数据,你要做的就是把矩阵𝑊转换成一个向量,把所有𝑊矩阵转换成向量之后,做连接运算,得到一个巨型向量𝜃,该向量表示为参数𝜃,代价函数𝐽是所有𝑊和𝑏的函数,现在你得到了一个𝜃的代价函数𝐽(即𝐽(𝜃))。接着,你得到与𝑊和𝑏顺序相同的数据,你同样可以把 d W [ 1 ] dW^{[1]} dW[1]和 d b [ 1 ] db^{[1]} db[1]…… d W [ l ] dW^{[l]} dW[l]和 d b [ l ] db^{[l]} db[l]转换成一个新的向量,用它们来初始化大向量𝑑𝜃,它与𝜃具有相同维度。
同样的,把 d W [ 1 ] dW^{[1]} dW[1]转换成矩阵, d b [ 1 ] db^{[1]} db[1]已经是一个向量了,直到把 d W [ l ] dW^{[l]} dW[l]转换成矩阵,这样所有的𝑑𝑊都已经是矩阵,注意 d W [ 1 ] dW^{[1]} dW[1]与 W [ 1 ] W^{[1]} W[1]具有相同维度, d b [ 1 ] db^{[1]} db[1]与 b [ 1 ] b^{[1]} b[1]具有相同维度。经过相同的转换和连接运算操作之后,你可以把所有导数转换成一个大向量𝑑𝜃,它与𝜃具有相同维度,现在的问题是𝑑𝜃和代价函数𝐽的梯度或坡度有什么关系?

这就是实施梯度检验的过程,英语里通常简称为“grad check”,首先,我们要清楚𝐽是超参数𝜃的一个函数,你也可以将𝐽函数展开为𝐽(𝜃1, 𝜃2, 𝜃3, … … ),不论超级参数向量𝜃的维度是多少,为了实施梯度检验,你要做的就是循环执行,从而对每个𝑖也就是对每个𝜃组成元素计算𝑑𝜃approx[𝑖]的值,我使用双边误差,也就是
d θ a p p r o x [ i ] = J ( θ 1 , θ 2 , . . . . . . θ i + ε , . . . ) − J ( θ 1 , θ 2 , . . . . . . θ i − ε , . . . ) 2 ε dθ_{approx}[i] =\frac{J(θ_1,θ_2,......θ_i+ε,...) - J(θ_1,θ_2,......θ_i-ε,...)}{2ε} dθapprox[i]=2εJ(θ1,θ2,......θi+ε,...)−J(θ1,θ2,......θi−ε,...)
只对 θ i θ_i θi增加𝜀,其它项保持不变,因为我们使用的是双边误差,对另一边做同样的操作,只不过是减去𝜀,𝜃其它项全都保持不变。

从上节课中我们了解到这个值( d θ a p p r o x [ i ] dθ_{approx}[i] dθapprox[i])应该逼近𝑑𝜃[𝑖]=𝜕𝐽/𝜕𝜃𝑖,𝑑𝜃[𝑖]是代价函数的偏导数,然后你需要对𝑖的每个值都执行这个运算,最后得到两个向量,得到𝑑𝜃的逼近值 d θ a p p r o x dθ_{approx} dθapprox,它与𝑑𝜃具有相同维度,它们两个与𝜃具有相同维度,你要做的就是验证这些向量是否彼此接近。
具体来说,如何定义两个向量是否真的接近彼此?我一般做下列运算,计算这两个向量的距离,𝑑𝜃approx[𝑖] − 𝑑𝜃[𝑖]的欧几里得范数,注意这里(||𝑑𝜃approx − 𝑑𝜃||2)没有平方,它是误差平方之和,然后求平方根,得到欧式距离,然后用向量长度归一化,使用向量长度的欧几里得范数。分母只是用于预防这些向量太小或太大,分母使得这个方程式变成比率,我们实际执行这个方程式,𝜀可能为 1 0 − 7 10^{−7} 10−7,使用这个取值范围内的𝜀,如果你发现计算方程式得到的值为 1 0 − 7 10^{−7} 10−7或更小,这就很好,这就意味着导数逼近很有可能是正确的,它的值非常小。
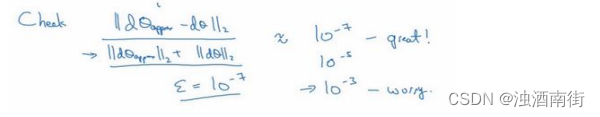
如果它的值在 1 0 − 5 10^{−5} 10−5范围内,我就要小心了,也许这个值没问题,但我会再次检查这个向量的所有项,确保没有一项误差过大,可能这里有 bug。
如果左边这个方程式结果是 1 0 − 3 10^{−3} 10−3,我就会担心是否存在 bug,计算结果应该比 1 0 − 3 10^{−3} 10−3小很多,如果比 1 0 − 3 10^{−3} 10−3大很多,我就会很担心,担心是否存在 bug。这时应该仔细检查所有𝜃项,看是否有一个具体的𝑖值,使得𝑑𝜃approx[𝑖]与𝑑𝜃[𝑖]大不相同,并用它来追踪一些求导计算是否正确,经过一些调试,最终结果会是这种非常小的值( 1 0 − 7 10^{−7} 10−7),那么,你的实施可能是正确的。

在实施神经网络时,我经常需要执行 foreprop 和 backprop,然后我可能发现这个梯度检验有一个相对较大的值,我会怀疑存在 bug,然后开始调试,调试,调试,调试一段时间后,我得到一个很小的梯度检验值,现在我可以很自信的说,神经网络实施是正确的。
现在你已经了解了梯度检验的工作原理,它帮助我在神经网络实施中发现了很多 bug,希望它对你也有所帮助。
这篇关于吴恩达深度学习笔记:深度学习的 实践层面 (Practical aspects of Deep Learning)1.13-1.14的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






