本文主要是介绍MATLAB实现杜拉德公式和凯夫公式的计算固液混合料浆临界流速,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
MATLAB实现杜拉德公式和凯夫公式的计算固液混合料浆临界流速:
杜拉德公式是用来计算非均质固液混合料浆在输送管中的临界速度的公式,具体形式为:
uL = FL × (2gD / (ρ0 - ρ1))^(1/2)
其中:
- uL:表示料浆的临界速度,单位为m/s,这是我们需要计算的目标值。
- g:表示重力加速度,通常取值为9.81m/s²。
- D:表示输送管的内径,单位为m。
- ρ0:表示固体物料的真实密度,单位为t/m³。
- ρ1:表示载体的密度,也就是液体部分的密度,单位为t/m³。
- FL:是一个速度系数,与以体积计的料浆固含量、料浆中的固体粒度有关,可以从图1中查得。
杜拉德公式主要考虑了固体物料的真实密度、输送管的内径、载体的密度以及一个与料浆固含量和固体粒度有关的速度系数,来计算非均质固液混合料浆在输送管中流动时,为了防止固体物料沉降到管壁上造成堵塞所需的临界速度。
凯夫公式:
uL = 1.04D^0.3 × (ρ0 - 1)^0.75 × ln(d50/16) × ln(60/CV)^0.13
凯夫公式是一个用于计算非均质固液混合料浆在输送管中临界速度的公式,特别适用于管径大于200mm的情况。
公式形式为:uL=FL 2gDρ0-ρ1 ρ1,其中uL代表料浆的临界速度(m/s),g是重力加速度(通常取9.81m/s^2),D是输送管内径(m),ρ0是固体物料的真实密度(t/m^3),ρ1是载体的密度(t/m^3),FL是与以体积计的料浆固含量、料浆中的固体粒度有关的速度系数。
变量解释:
uL:料浆的临界速度,指为了防止料浆中的固体物料沉降到管壁上而造成输送管堵塞,料浆在输送管中必须达到的最小流动速度。
g:重力加速度,地球上的物体在自由落体时受到的加速度,是一个常数。
D:输送管内径,即管道内部的直径,决定了管道的流量和料浆在其中流动的路径大小。
ρ0:固体物料的真实密度,指单位体积内固体物料的质量,是计算料浆流动特性时的重要参数。
ρ1:载体的密度,即料浆中液体部分的密度,同样对料浆的流动特性有重要影响。
FL:速度系数,与料浆的固含量和固体粒度有关,用于调整公式以反映不同料浆的流动特性。
MATLAB代码如下:
clc;clear all;close all;warning off;%关闭警报
rand('seed', 100);
randn('seed', 100);
format long g;% 假设的参数值
g = 9.81; % 重力加速度, m/s^2
D = 0.1; % 管道直径, m
rho0 = 2700; % 固体物料的真实密度, kg/m^3 (例如:铝)
rho1 = 1000; % 载体的密度, kg/m^3 (例如:水)
FL = 1.6; % 速度系数,根据实际情况调整% 固含量范围 (例如:从0.1到0.6)
D_range = 0.1:0.05:0.6;% 初始化临界速度数组
uL_durand = zeros(size(D_range));% 计算临界速度
for i = 1:length(D_range)D=D_range(i);% 杜拉德公式uL_durand(i) = FL * (2*g*D / (rho0 - rho1))^(1/2);
end% 绘制图表
figure;
plot(D_range, uL_durand);
xlabel('管径D(m)');
ylabel('临界速度 uL (m/s)');
grid on;
title('杜拉德公式计算的临界速度与管径的关系');% 假设的参数值
D = 0.1; % 管道直径, m
rho0 = 2700; % 固体物料的真实密度, kg/m^3 (例如:铝)
d50 = 0.001; % 细粒累积量为50%的固体物料的粒度, m% 固含量范围 (例如:从0.1到0.6)
CV_range = 0.1:0.05:0.6;% 初始化临界速度数组
uL_cave = zeros(size(CV_range));% 计算临界速度
for i = 1:length(CV_range)% 凯夫公式uL_cave(i) = 1.04 * D^0.3 * (rho0 - 1)^0.75 * log(d50/16) * log(60/CV_range(i))^0.13;
end% 绘制图表
figure;
plot(CV_range, uL_cave);
xlabel('固含量 CV');
ylabel('临界速度 uL (m/s)');
grid on;
title('凯夫公式计算的临界速度与固含量的关系');程序结果:

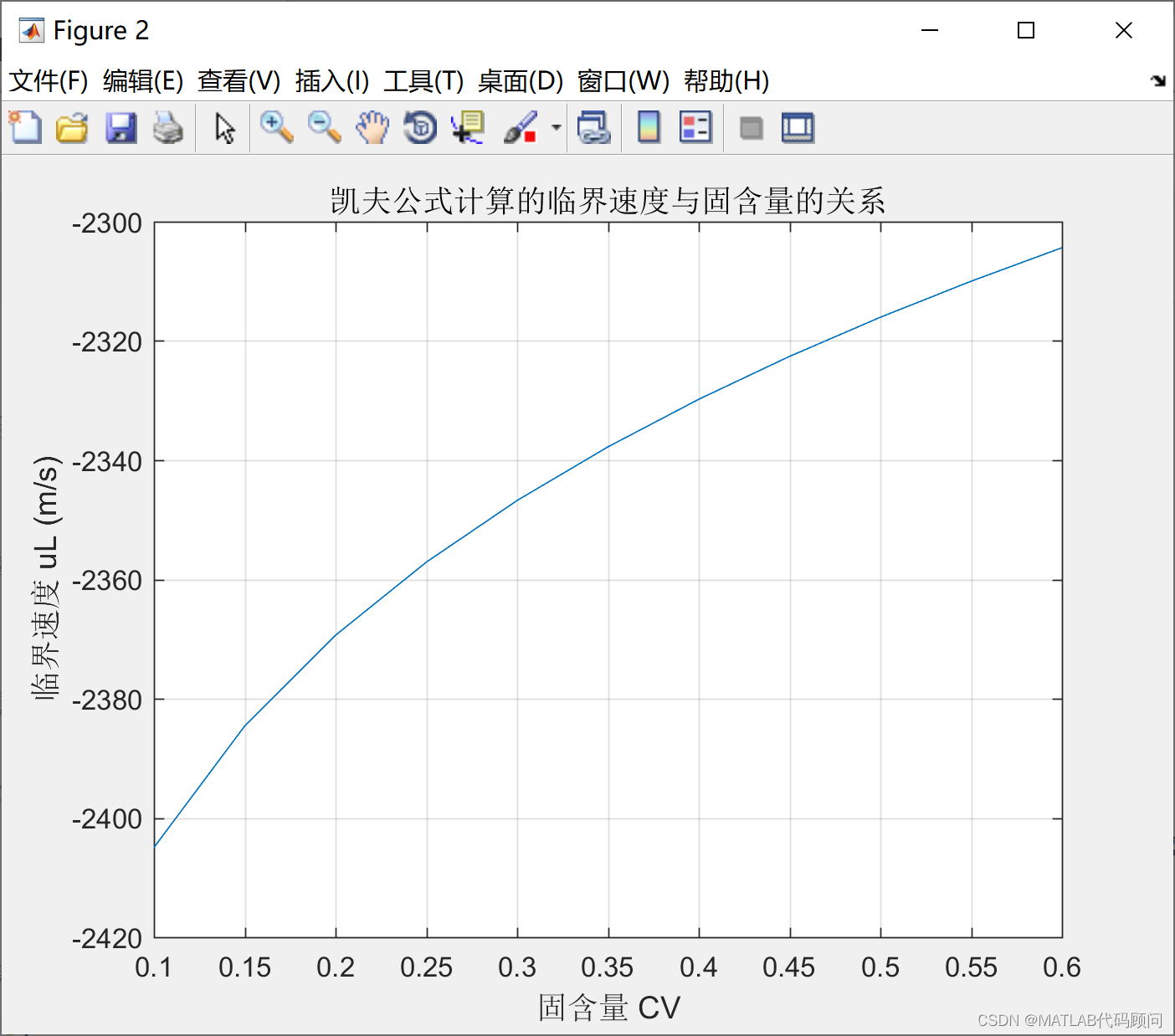
这篇关于MATLAB实现杜拉德公式和凯夫公式的计算固液混合料浆临界流速的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




