力扣每日一题109：有序链表转换二叉搜索树

本文主要是介绍力扣每日一题109：有序链表转换二叉搜索树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

中等

给定一个单链表的头节点  head ，其中的元素 按升序排序 ，将其转换为 

平衡

 二叉搜索树。

示例 1:

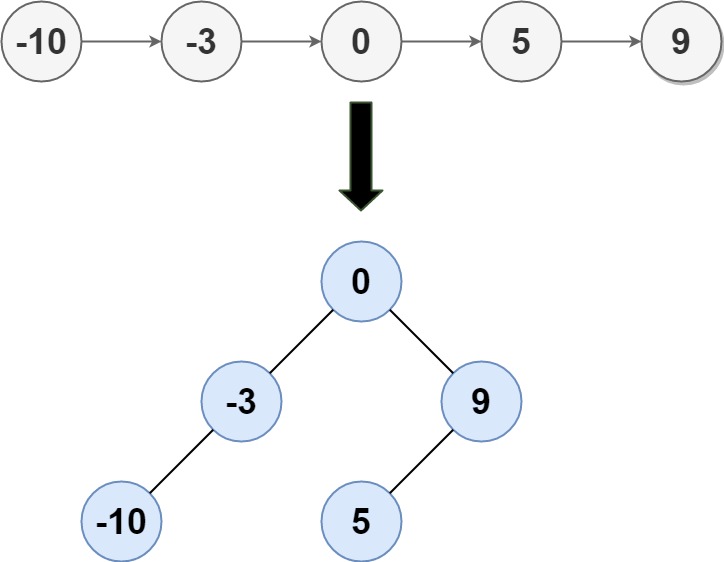
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。

示例 2:

输入: head = []
输出: []

提示:

• head 中的节点数在[0, 2 * 104] 范围内
• -105 <= Node.val <= 105

---

面试中遇到过这道题?

1/5

是

否

通过次数

161.6K

提交次数

211K

通过率

76.6%

思路

和有序数组转换为二叉搜索树的的思路一样，都是以中间值为根，然后递归建立左右子树。区别就是：如果是数组的话，直接用下标就能找到中间元素，如果是有序链表的话，用快慢指针寻找中间元素、或是知道链表长度情况下，根据遍历次数寻找中间元素。

链表和树的结点结构

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*//*

方法一：根据遍历次数寻找中间元素。

class Solution {
public:TreeNode *build(ListNode *head,int lo,int hi){if(lo>hi) return NULL;//找中间位置int mid=(lo+hi)/2;ListNode *middle=head;for(int i=0;i<mid-lo;i++){middle=middle->next;}//建根，递归建立左右子树TreeNode *root=new TreeNode(middle->val);root->left=build(head,lo,mid-1);root->right=build(middle->next,mid+1,hi);return root;}TreeNode* sortedListToBST(ListNode* head) {int n=0;ListNode *p=head;while(p){n++;p=p->next;}return build(head,0,n-1);}
};

方法二：快慢指针寻找中间元素

使用快慢指针寻找中间元素是链表题目的基操。原理就是，设置一个快指针fast和一个慢指针slow，快指针的速度是慢指针的两倍，当快指针走到最后的时候，慢指针就到了中间位置。

class Solution {
public:ListNode* getMedian(ListNode* left, ListNode* right) {ListNode* fast = left;ListNode* slow = left;while (fast != right && fast->next != right) {fast = fast->next;fast = fast->next;slow = slow->next;}return slow;}TreeNode* buildTree(ListNode* left, ListNode* right) {if (left == right) {return nullptr;}ListNode* mid = getMedian(left, right);TreeNode* root = new TreeNode(mid->val);root->left = buildTree(left, mid);root->right = buildTree(mid->next, right);return root;}TreeNode* sortedListToBST(ListNode* head) {return buildTree(head, nullptr);}
};

方法三：分治+中序遍历优化

上面的两种方法都是先找到中间节点，再递归建立左右子树，属于先序遍历。这样，每次寻找中间节点时，就要logn的时间复杂度，总的时间复杂度变成了O(nlogn)。

如果我们可以用中序遍历，先建立左子树，左子树建完再建根，然后再建右子树，那么就省去了查找中间节点的时间，时间复杂度就变成了O(n)。

也就是说，我们没有必要“先”找到中间节点：我们可以先构建了左子树，建立结束后，指针自然指向中间结点。那么如何构建左子树呢？其实我们只需要确定子树的大小就可以。所以先用O(n)的时间计算链表长度，之后用中序遍历。当然，指针需要是“引用”，这样才能改变指针的指向，实现建好左子树后，指针自然指向中间结点。

下面是官方题解：

class Solution {
public:int getLength(ListNode* head) {int ret = 0;for (; head != nullptr; ++ret, head = head->next);return ret;}TreeNode* buildTree(ListNode*& head, int left, int right) {if(left>right) return NULL;int mid=(left+right)/2;TreeNode *root=new TreeNode();root->left=buildTree(head,left,mid-1);root->val=head->val;head=head->next;root->right=buildTree(head,mid+1,right);return root;}TreeNode* sortedListToBST(ListNode* head) {int length = getLength(head);return buildTree(head, 0, length - 1);}
};

时间复杂度：O(n)，其中 n 是链表的长度。

设长度为 n 的链表构造二叉搜索树的时间为 T(n)，递推式为 T(n)=2⋅T(n/2)+O(1)，根据主定理，T(n)=O(n)。

空间复杂度：O(log⁡n)，这里只计算除了返回答案之外的空间。平衡二叉树的高度为 O(log⁡n)，即为递归过程中栈的最大深度，也就是需要的空间。

这篇关于力扣每日一题109：有序链表转换二叉搜索树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---