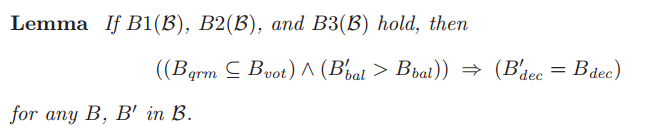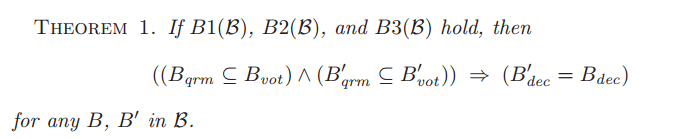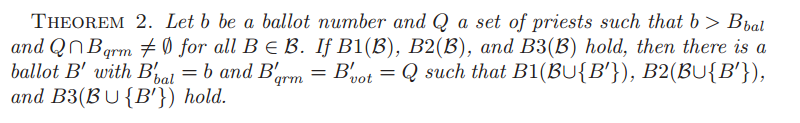本文主要是介绍Paxos协议学习---2.由3大条件证明一致性,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Paxos是分布式的一致性协议,最重要的部分当然是这个一致性的证明。
在朴素Paxos协议中给出了3大条件,只要达到了这3大条件
可以证明,如果Paxos协议达成了一次成功的表决,那么这个表决具有一致性。
需要说明的是,这3大条件并不保证进行性,也就是说并不保证一定会达成成功的表决。
但是可以保证的是,如果达成了一个成功表决,那么这个表决具有一致性。
1.基本术语
(1)
ballot/B表决
decree法令
quorum法定人数集、多数派
Bdec某次表决的法令
Bqrm参与某次表决的牧师集合
Bvot参与某次表决的牧师中投赞成票的集合
Bbal某次表决的编号
说明1:成功的表决
说一轮表决B是成功的,当且仅当Bqrm属于Bvot
即该轮表决中所有参与的牧师都投了赞成票
说明2:表决的大小
B1 > B2 等价于 B1val > B2val,
但是这个下标并不反映实际表决发生的顺序。
即允许bal小的表决发生在bal大的之后
(2)
要最终确定一个值需要多轮表决。
某次表决B
多轮表决构成的集合是β
V表示一个投票
Vbal表示投票的编号
Vpst表示投票的牧师
Vvec表示投票的法令
V1<V2等价于,V1bal<V2bal
Votes(β)表示所有在β中的投票
p表示一个牧师
b表示一个表决的编号
MaxVote(b,p,β)表示β中,由p投出的所有表决中,编号小于b
的投票中最大的投票v。
Q表示牧师集合
MaxVote(b,Q,β)表示,所有p属于Q中MaxVote(b,p,β)的最大值
2.MaxVote(b,Q,β)
MaxVote(b,Q,β)的意义十分重要,是接下来要介绍的三大条件以及后面一致性证明的核心概念。
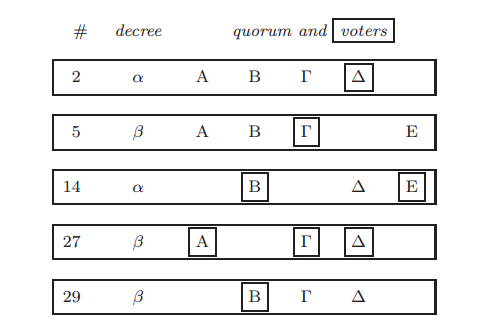
用一个例子来表述MaxVote(b,Q,β)的含义。
其中,最左边的#下面表示的是编号bal
然后decree表示的是需要表决的法令
接下来A、B、倒L、三角形、E表示所有可能来进行表决的牧师
每一行实际显示出的牧师就是Bqrm,牧师中的多数派
每一行被方框框住的牧师就是Bvot,Bqrm中实际在某次表决中投赞成票的牧师。
MaxVote(2,{A、B、倒L、三角形},β) bal == null
MaxVote(5,{A、B、倒L、E},β) bal == null
MaxVote(14,{B、三角形、E},β) bal == 2 ,其中关联牧师为三角形
MaxVote(27,{A、倒L、三角形},β) bal == 5 ,其中关联牧师为倒L
MaxVote(29,{B、倒L、三角形},β)bal == 27 ,其中关联牧师为倒L、三角形
3.三大条件
条件1:β中的每一轮表决,都有一个唯一的编号
条件2:β中任意两轮的B1qrm和B2qrm中,至少有一个公共的牧师成员
条件3:对于每一轮表决B,如果B的Bqrm中任何一个牧师在β中一个编号更小的表决中投过赞成票,
那么B的法令必须与所有更小轮表决中的最大那次的表决的法令相同
条件2的笔记:
由于有公共假设,牧师如果没有出去旅游,就会来办公,
并且如果同时有超过总数量一半的牧师不来,就是无法确定一个法令。
所以条件2又可以表述为
任意一次的Bqrm都是超过牧师总数量的一半的。
即Bqrm始终要是总人数的多数派这次表决才能生效。
条件3的笔记:
(1)
相对于条件1和2的好理解,
这个条件3仿佛是不知怎么样就出现的一个古怪约束。
然而这才是重头戏,要保证一致性,这个条件3是相当重要的。
(2)
假设本次表决编号N,现在有牧师1-k,
它们投过票的表决编号为N1-Nk,
条件3就是要保证,N1-Nk都小于N,
然后选出N1-Nk中最大的那个编号对应的表决的法令作为本次表决的法令
这个条件结合MaxVote(b,Q,β)与上面的图更好理解一些。
三大条件更正式的表述如下:
4.引理与定理
(1)引理1
在3大条件被满足的情况下,如果β中的表决B是成功的,那么β中更大编号的表决和B有相同的法令。
(2)定理1
在3大条件被满足的情况下,任意两轮成功的表决,都是对相同法令的表决。
(3)定理2
在3大条件被满足的情况下,是有可能做出一次成功的表决的。
但不能保证一定会产生一轮成功的表决。
但至少表明在3大条件的基础上表决协议不会产生死锁。
引理与定理的正式表述:
(1)引理1
(2)定理1
(3)定理2
思考:
(1)由定理1很容易理解如果产生了成功的表决,那么表决具有一致性。
因为所有成功的表决都是对相同的法令进行的表决。
(2)由引理1很容易证明定理1
因为所有不同的成功的表决的编号都是不同的,这一点由条件1保证。
那么假设成功表决中编号最大的表决时B,那么由引理1可知,任一成功的表决的法令都与B相同。
所以任一成功的表决的法令是相同的。
5.证明一致性
由4中的思考的(1)、(2)可知,证明朴素Paxos如果成功表决,那么其结果具有一致性的证明的关键是引理1的证明。
论文中采用的是反证法证明。
引理1说如果满足条件1-3,并且B是一次通过的表决,那么所有编号比Bbal大的表决的法令和Bdec相同。
假设:存在集合X,X为比B编号大,并且法令与Bdec不同的表决的集合。
进一步假设C是X中编号最小的一个表决。
通过一系列的推导,可以得出
MaxVote(Cbal,Cqrm,β)属于集合X
并且MaxVote(Cbal,Cqrm,β)bal < Cbal
这是矛盾的。
我们令MaxVote(Cbal,Cqrm,β)=D
那么D属于集合X,并且Dbal < Cbal
但是我们之前的假设就是C是集合X中bal最小的。
所以矛盾。
那么假设不成立,那么命题引理1得证。
正式的推导:
说明:
步骤3.因为B是一次成功的投票,所以Bvot==Bqrm,又因为C也是一次β中的投票所以Cqrm也是多数派。
所以Bvot与上Cqrm == Bqrm与上Cqrm != 空集
步骤4.因为C是属于集合X的,而集合X的定义又是bal大于Bbal的,
并且MaxVote(Cbal,Cqrm,β)bal的定义是所有比Cbal小的里面最大的。
所以MaxVote(Cbal,Cqrm,β)bal大于等于Bbal
步骤5、6.由步骤4可知MaxVote(Cbal,Cqrm,β)bal >= Bbal
所以无论如何MaxVote不是nullVote,那么根据条件3就可以推出步骤6
这篇关于Paxos协议学习---2.由3大条件证明一致性的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!