本文主要是介绍[Algorithm][堆][优先级队列][最后一块石头的重量][数据流中的第K大元素][前K个高频单词][数据流中的中位数]详细讲解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 1.最后一块石头的重量
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.数据流中的第 K 大元素
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 3.前K个高频单词
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 4.数据流的中位数
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.最后一块石头的重量
1.题目链接
- 最后一块石头的重量
2.算法原理详解
- 思路:利用大根堆
- 将所有的⽯头放⼊⼤根堆中
- 每次拿出前两个堆顶元素粉碎⼀下,如果还有剩余,就将剩余的⽯头继续放⼊堆中
3.代码实现
int LastStoneWeight(vector<int>& stones)
{priority_queue<int> heap; // STL默认大根堆for(auto& x : stones){heap.push(x);}// 模拟过程while(heap.size() > 1){int a = heap.top();heap.pop();int b = heap.top();heap.pop();if(a > b){heap.push(a - b);}}return heap.size() ? heap.top() : 0;
}
2.数据流中的第 K 大元素
1.题目链接
- 数据流中的第 K 大元素
2.算法原理详解
- 本题为TOP-K的运用
- TOP-K问题,一般用一下两种方法来解决
- 堆: O ( N ∗ l o g K ) O(N*logK) O(N∗logK)
- 快速选择算法: O ( N ) O(N) O(N)
- 用堆解决TOP-K问题
- 用数据集合中前K个元素来建堆
- 前k个最大的元素:建小堆
- 前k个最小的元素:建大堆
- 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
- 走完以后,堆里面的k个数,就是最大的前k个
- 用数据集合中前K个元素来建堆
- 流程:
- 创建一个大小为k的堆(大根堆/小根堆)
- 循环
- 依次进堆
- 判断堆的大小是否超过k
- 如何判断是否用大根堆还是小根堆,为什么呢?
- TOP-K-MAX:建小堆
- 依次进堆,当
heap.size() > k时,弹出堆顶元素 - 因为堆顶元素是最小的,绝对不会是TOP-K-MAX
- 依次进堆,当
- TOP-K-MIN:建大堆
- 依次进堆,当
heap.size() > k时,弹出堆顶元素 - 因为堆顶元素是最大的,绝对不会是TOP-K-MIN
- 依次进堆,当
- TOP-K-MAX:建小堆
3.代码实现
class KthLargest
{// 创建一个大小为k的小根堆priority_queue<int, vector<int>, greater<int>> heap;int _k = 0;
public:KthLargest(int k, vector<int>& nums) {_k = k;for(auto& x : nums){heap.push(x);if(heap.size() > _k){heap.pop();}}}int add(int val) {heap.push(val);if(heap.size() > _k){heap.pop();}return heap.top();}
};
3.前K个高频单词
1.题目链接
- 前K个高频单词
2.算法原理详解
- 思路:利用"堆"来解决TOP-K问题
- 预处理原始的字符串数组
- 哈希表统计每一个单词出现的频次
- 创建一个大小为k的堆
- 频次:小根堆
- 字典序(频次相同的时候):大根堆
- 循环
- 让元素一次进堆
- 判断
- 提取结果
- 把数组逆序
- 预处理原始的字符串数组
3.代码实现
class Solution
{typedef pair<string, int> PSI;struct Cmp{bool operator()(PSI& a, PSI& b){// 频次相同,字典序按大根堆排序if(a.second == b.second){return a.first < b.first;}// 频次按小根堆排序return a.second > b.second;}};
public:vector<string> TopKFrequent(vector<string>& words, int k) {// 统计每个单词出现的次数unordered_map<string, int> hash;for(auto& str : words){hash[str]++;}// 创建一个大小为k的堆priority_queue<PSI, vector<PSI>, Cmp> heap;// TOP-Kfor(auto& psi : hash){heap.push(psi);if(heap.size() > k){heap.pop();}}// 提取结果,逆序heapvector<string> ret(k);for(int i = k - 1; i >= 0; i--){ret[i] = heap.top().first;heap.pop();}return ret;}
};
4.数据流的中位数
1.题目链接
- 数据流的中位数
2.算法原理详解
-
思路一:直接
sort- 时间复杂度:
add(): O ( N ∗ l o g N ) O(N*logN) O(N∗logN)find(): O ( 1 ) O(1) O(1)
- 每次
add(),都sort一遍,时间复杂度很恐怖
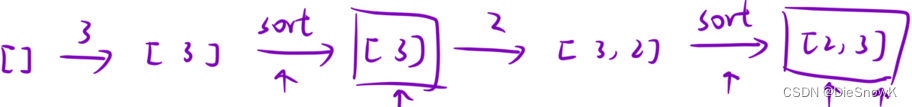
- 时间复杂度:
-
思路二:插入排序的思想
- 时间复杂度:
add(): O ( N ) O(N) O(N)find(): O ( 1 ) O(1) O(1)
- 每次
add(),都在原数据基础上进行插入排序,时间复杂度有所改善

- 时间复杂度:
-
思路三:利用大小堆来维护数据流中位数
- 此问题时关于**「堆」的⼀个「经典应⽤」**
- 时间复杂度:
add(): O ( l o g N ) O(logN) O(logN)find(): O ( 1 ) O(1) O(1)
- 将整个数组「按照⼤⼩」平分成两部分(如果不能平分,那就让较⼩部分的元素多⼀个)
m == nm > n -> m == n + 1
- 将左侧部分放⼊「⼤根堆」中,然后将右侧元素放⼊「⼩根堆」中
- 这样就能在 O ( 1 ) O(1) O(1)的时间内拿到中间的⼀个数或者两个数,进⽽求的平均数
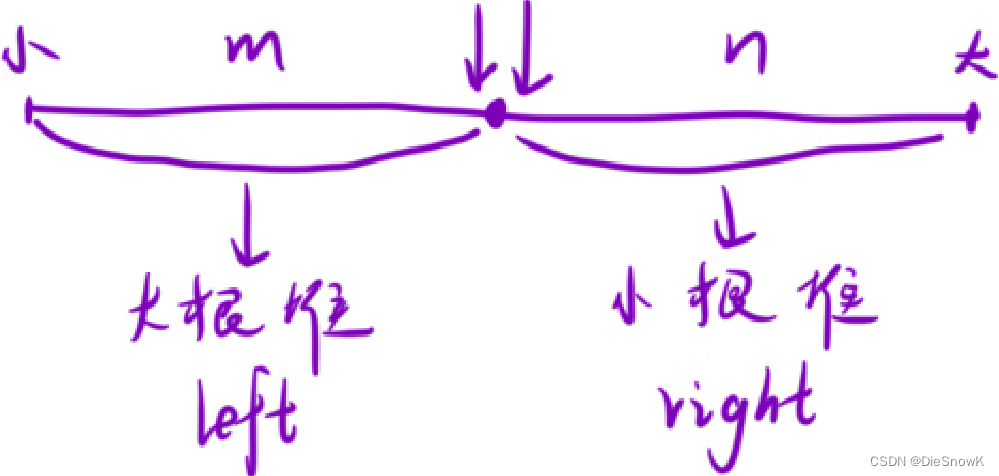
-
细节:
add()时,如何维护m == n || m > n -> m == n + 1?-
m == n
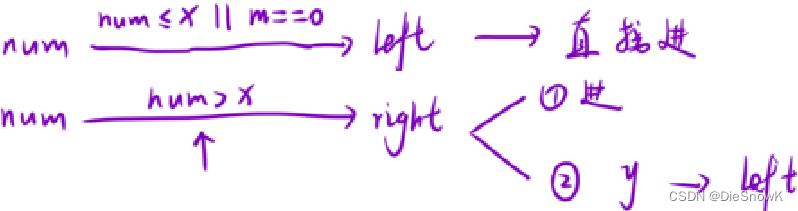
-
m > n -> m == n + 1
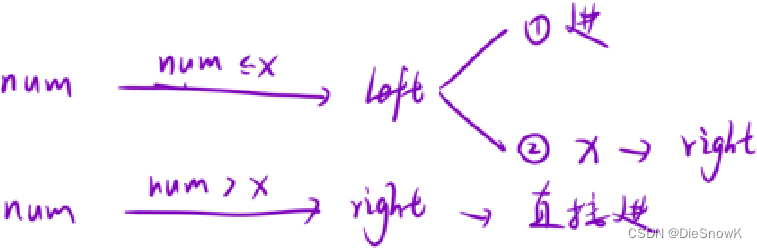
-
3.代码实现
class MedianFinder
{priority_queue<int> left; // 大根堆priority_queue<int, vector<int>, greater<int>> right; // 小根堆
public:MedianFinder() {}void AddNum(int num) {if(left.size() == right.size()){if(left.empty() || num <= left.top()){left.push(num);}else{right.push(num);left.push(right.top());right.pop();}}else{if(num <= left.top()){left.push(num);right.push(left.top());left.pop();}else{right.push(num);}}}double FindMedian() {if(left.size() == right.size()){return (left.top() + right.top()) / 2.0;}else{return left.top();}}
};
这篇关于[Algorithm][堆][优先级队列][最后一块石头的重量][数据流中的第K大元素][前K个高频单词][数据流中的中位数]详细讲解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




