本文主要是介绍[编程之美] PSet2.8 找符合条件的整数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
题目：
任意给定一个正整数N，求一个最小的正整数M(M>1)，使得N*M的十进制表示形式里只含有1和0。
方法一：
暴力枚举：给定N，令M从2开始，枚举M的值直到遇到一个M使得N*M的十进制表示中只有1和0.
方法二：
换一种枚举方法，我们枚举N*M的取值效果怎么样呢？因为N * M的只包含1和0，所以对于K位的N*M，需要搜索2的K次方。
因为找的是最小整数，所以可以采用BFS（宽度优先搜索）。
当N = 3时，看如下搜索树，括号内容表示mod N的值：
因为数字N*M只含有0和1，所以直接遍历1,10,11,100,101······，一直找，找到一个能被N整除的数就返回。
方法三：
将方法二的解空间按模N余数分类，只保存最小的同余数，使得搜索的解空间由2^K降低至N，假设有两个数X和Y，X的下一分支是10*X以及10*X+1，Y的下一分支是10*Y以及10*Y+1，那么10*X与10*Y对N同余（看做10个X相加对N取余，结果和10个Y相加对N取余相同），同样10*X+1和10*Y+1对N同余，所以X的后面分支和Y的后面分支对N余数相同，如果X<Y，因为题意关注最小的对N取余为0的数，则在这个情况下只需要关注X以及它的分支就可以了。可以剪去Y和Y的分支。
下面是N=9时搜索空间
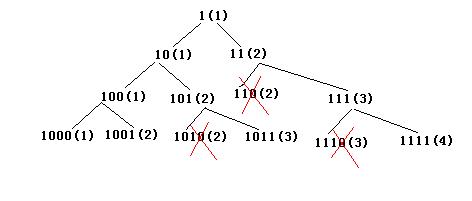
如果依照方法二进行搜索，在第4层将会有2^(K-1)=8个节点待搜索，此时只需要最多搜索N个节点就行了。
下面是实现代码：
/*
问题描述：对于给定的整数N找到一个整数M，使得N*M中只含有0与1
解法：对于一个只含有0与1的整数，找到对于给定的N取余等于0的这个整数X，此时M=X/N;
用一个二维数组vector<vector<int>> BigInt来计数，即BigInt[i]来存储余数为i的当前层最小数字，每迭代一层当前数字翻10倍
因为数字只由0与1构成，即BigInt[(i+k) % N].push_back(i);
*/
void printVec(const vector<int> &vec)
{int temp = -1;for(int i=vec.size()-1 ; i>=0 ; i--){//高次幂决定1的位置cout<<"1";temp = vec[i];while(i>0 && --temp!=vec[i-1])//防止越界，弹出循环时下标指向第一个元素cout<<"0";}while(temp--)cout<<"0";cout<<endl;
}
void findInt(int N)
{int M =-1;vector<vector<int>>BigInt;for(int i=0 ; i<N ; i++){//初始化BigInt二维数组vector<int> temp;temp.clear();BigInt.push_back(temp);}BigInt[1].push_back(0);//10^0=1,1对任何正整数数取余都等于1,接下来最小符合条件正整数从10开始int i,j;int noUpdate = 0;for(i=1,j=10%N ; ; i++,j=(j*10)%N){//开始从10^1遍历，i表示10的幂次位数，j表示当前幂次对N的取余信息bool updateFlag = false;if(BigInt[j].size() == 0){//初始化updateFlag = true;BigInt[j].clear();BigInt[j].push_back(i);}for(int k=0 ; k<BigInt.size() ; k++){//遍历所有计数数组if(BigInt[k].size()>0 && BigInt[(j+k)%N].size()==0 && i>BigInt[k][BigInt[k].size()-1]){//更新条件,注意最后一个条件的含义在于从10跳到100而不是跳到20updateFlag = true;BigInt[(j+k)%N] = BigInt[k];BigInt[(j+k)%N].push_back(i);}}//循环迭代N次都没有计数数组的数据被更新，说明无解；或是BigInt[0].size()>0找到了解，跳出循环if(updateFlag == false)//每一轮迭代，只要没有更新数据就计数加1noUpdate++;if(noUpdate==N || BigInt[0].size()>0){break;}}if(BigInt[0].size() > 0){//找到解printVec(BigInt[0]);return;}else{cerr<<"M not exit !"<<endl;return ;}
}int main()
{findInt(6);return 0;
}
扩展问题：
1.对于任意的N，一定存在M，使得N*M的乘积的十进制表示只有0和1吗？
解答：一定有解，而且不唯一。
对于数列：
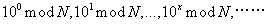是一个无穷数列，但是每一个元素都在[0,N-1]之中，所以必然存在循环节。假设10^s%N = 10^t%N，且s<t，那么t-s是循环节长度，所以：
因此将这N项相加必然等于0(mod N)，举个例子：
10%6 = 100%6 = 1000%6 = 10000%6···(mod N)，因此6个数相加得1111110，而且1111110%6=0。
2.怎么找出满足题目要求（N*M十进制表示形式中只含1和0）的N和M，使得N * M < 2的16次方，且N+M最大？
解答：由于N固定，于是要N+M最大只需要求 最大的在2^16范围内的且只含1和0的整数X，然后用X/M即可。可以在原方法三的基础上改变成对N的同余数只保留最大的那些，保存本次迭代得到的对N取余为0的那个整数为temp，再向下迭代找到下一个对N取余为0的那个整数，如果下一个满足条件的整数比2^16要小，就更新temp为这次迭代的整数，继续下去···，直到有一次迭代的对N取余为0的整数大于2^16，输出temp也就是上次迭代的结果。
参考资料：http://blog.csdn.net/i_code/article/details/7408606
这篇关于[编程之美] PSet2.8 找符合条件的整数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
