本文主要是介绍代码随想录Day 36|Python|Leetcode|01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
01背包问题,你该了解这些!
46. 携带研究材料(第六期模拟笔试) (kamacoder.com)
代码随想录 (programmercarl.com)
- 确定dp数组(dp table)以及下标的含义:dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
- 确定递推公式:
两个方向推出来dp[i][j],
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
- dp数组如何初始化:
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:

在看其他情况。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。

- 确定遍历顺序:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:

再来看看先遍历背包,再遍历物品呢,如图:

大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!
但先遍历物品再遍历背包这个顺序更好理解
- 举例推导dp数组:
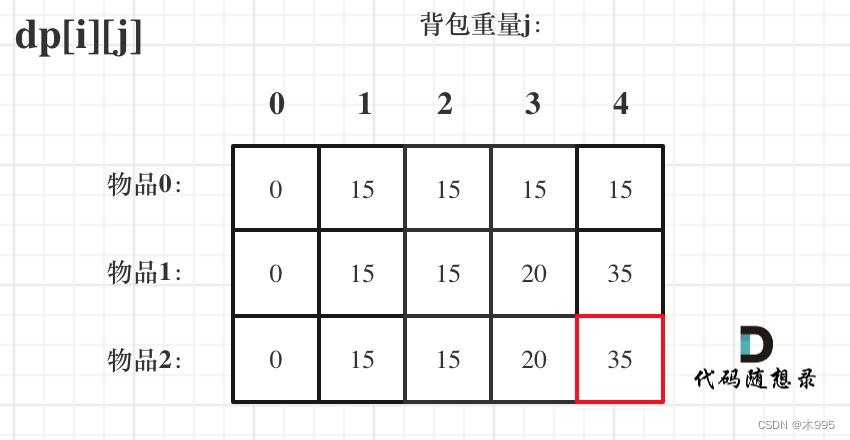
题目描述
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的空间,并且具有不同的价值。
小明的行李空间为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料只能选择一次,并且只有选与不选两种选择,不能进行切割。
输入描述
第一行包含两个正整数,第一个整数 M 代表研究材料的种类,第二个正整数 N,代表小明的行李空间。
第二行包含 M 个正整数,代表每种研究材料的所占空间。
第三行包含 M 个正整数,代表每种研究材料的价值。
输出描述
输出一个整数,代表小明能够携带的研究材料的最大价值。
注意代码为ACM模式,输入m为物品数横轴,n为重量,作为纵轴,矩阵尺寸应为mx(n+1),因为n多出了需要考虑重量是0的情况。
m, n = map(int, input().split())weights = list(map(int, input().split()))
values = list(map(int, input().split()))
#initialize
dp = [[0]*(n+1) for _ in range(m)]
#when n = 0, dp[i][0] = 0
for j in range(n+1):if weights[0]<=j:dp[0][j] = values[0]else:dp[0][j] = 0
def bag():for i in range(1,m):for j in range(1,n+1):if j<weights[i]:dp[i][j] = dp[i-1][j]else:dp[i][j] = max(dp[i-1][j], dp[i-1][j-weights[i]]+values[i])return dp[m-1][n]
print(bag())01背包问题,你该了解这些! 滚动数组
- 确定dp数组的定义:在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
- 一维dp数组的递推公式:两种可能,一种是不放入物品i,及自身的价值dp[j],一种是放入物品i,dp[j-weights[i]]+values[i],所以dp[j] = max(dp[j], dp[j-weigts[i]]+values[i])
- 一维dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了
- 一维dp数组遍历顺序:从后向前,避免重复添加上一层数量,先遍历物品,再遍历背包。
- 举例推导dp数组
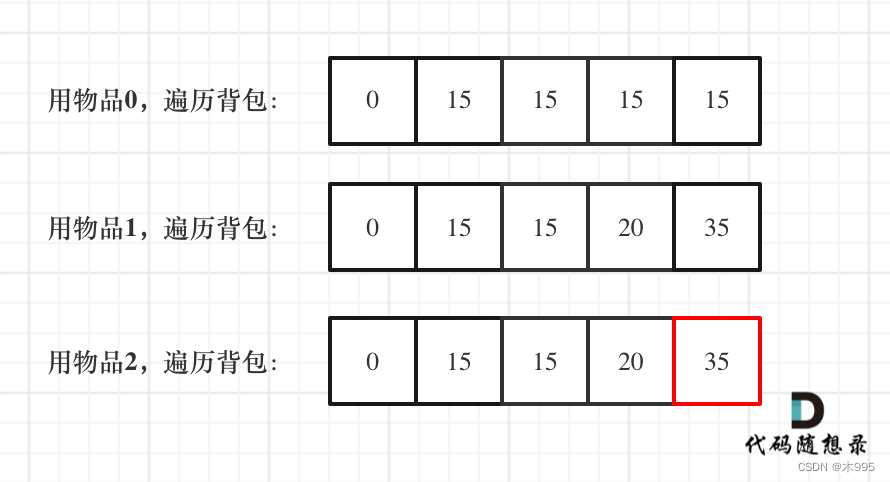
ACM代码:
m, n = map(int, input().split())
weights = list(map(int, input().split()))
values = list(map(int, input().split()))
#initialize
dp = [0]*(n+1) #1-dimensional array
def bag():for i in range(m):for j in range(n,weights[i]-1, -1):dp[j] = max(dp[j], dp[j-weights[i]]+values[i])return dp[n]
print(bag())416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
解题思路:
本题可以使用回溯或背包解答。可以将其看作一个nums,如果该数组能得到一个sum(nums)//2的子集,该数组可以拆成两个一样的子数集且和相等,return True。
类似于背包问题的解题思路,
1. 确认dp数组的定义:dp[j]当容量为j时的最大数之和(最大价值),需要注意的是,这里物品i和价值均为nums[i].
2. 一维dp推导公式:dp[j] = max(dp[j], dp[j-weights[i]]+values[i])
3. 一维dp数组如何初始化:dp[0] = 0
4. 一维dp数组遍历顺序:从后向前,避免重复添加上一层数量,先遍历物品,再遍历背包
5. 举例推导dp数组
代码:
class Solution:def canPartition(self, nums: List[int]) -> bool:if sum(nums)%2 != 0:return Falsetarget = sum(nums)//2#target is the largest bagweightdp = [0]*(target+1)for i in range(len(nums)):for j in range(target, nums[i]-1, -1):dp[j] = max(dp[j], dp[j-nums[i]]+nums[i])if dp[target] == target:return Truereturn False这篇关于代码随想录Day 36|Python|Leetcode|01背包问题,你该了解这些! ● 01背包问题,你该了解这些! 滚动数组 ● 416. 分割等和子集的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






