图论单源最短路径——spfa

本文主要是介绍图论单源最短路径——spfa，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【模板】单源最短路径（弱化版）

本题用的spfa

题目背景

本题测试数据为随机数据，在考试中可能会出现构造数据让SPFA不通过，如有需要请移步 P4779。

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入格式

第一行包含三个整数 $n,m,s$，分别表示点的个数、有向边的个数、出发点的编号。

接下来 $m$ 行每行包含三个整数 $u,v,w$，表示一条 $u\to v$ 的，长度为 $w$ 的边。

输出格式

输出一行 $n$ 个整数，第 $i$ 个表示 $s$ 到第 $i$ 个点的最短路径，若不能到达则输出 $2^{31}-1$。

样例 #1

样例输入 #1

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

样例输出 #1

0 2 4 3

提示

【数据范围】
对于 $20\%$ 的数据：$1\le n\le 5$，$1\le m\le 15$；
对于 $40\%$ 的数据：$1\le n\le 100$，$1\le m\le 10^4$；
对于 $70\%$ 的数据：$1\le n\le 1000$，$1\le m\le 10^5$；
对于 $100\%$ 的数据：$1\le n\le 10^4$，$1\le m\le 5\times 10^5$，$1\le u,v\le n$，$w\ge 0$，$\sum w<2^{31}$，保证数据随机。

Update 2022/07/29：两个点之间可能有多条边，敬请注意。

对于真正 $100\%$ 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

样例说明：

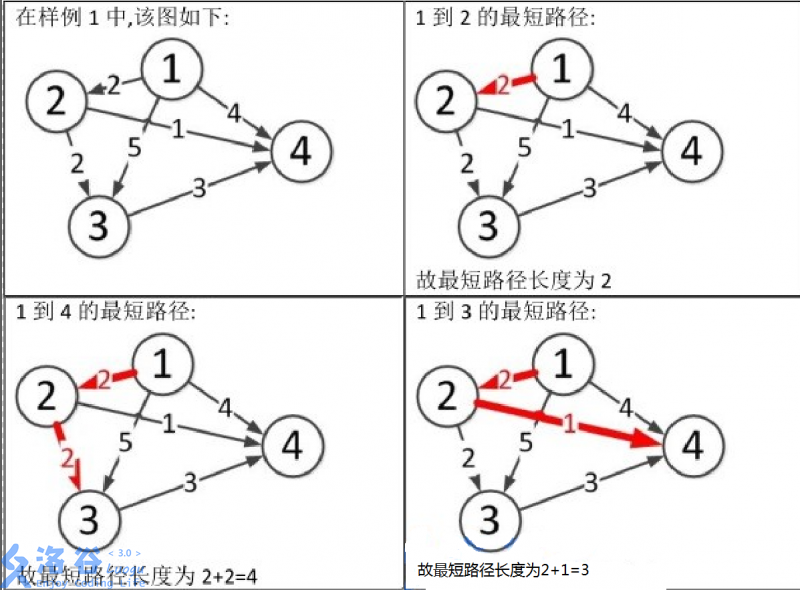
图片1到3和1到4的文字位置调换

代码：

/*
spfa 2024.4.28 SimonAN
*/
#include<iostream>
#include<bits/stdc++.h>
#define lyh(i,a,b) for(int i = a;i <= b;i ++)
#define hyl(i,a,b) for(int i = a;i >= b;i --)
#define debug(a) cout<<#a<<'='<<a<<endl;
#define endl "\n"
#define LL long long
#define INF 0x3f
using namespace std;
const int N = 5e5 + 100;
int n,m,s;
int h[N],e[N],ne[N],idx;
LL w[N];
int d[N];
void add(int a,int b,int c){e[idx] = b, w[idx] = c,ne[idx] = h[a], h[a] = idx ++;
}
int q[N];
int st[N];
int tt = -1,hh = 0;
void spfa(){d[s] = 0;q[++tt] = s, st[s] = 1;while(hh <= tt){int t = q[hh++];st[t] = 0;for(int k = h[t];k != -1;k = ne[k]){int ee = e[k];if(d[ee] > d[t] + w[k]){d[ee] = d[t] + w[k];if(st[ee] == 0){q[++tt] = ee; st[ee] = 1;}}}}
}
int main(){memset(d,0x3f3f3f,sizeof d);memset(h,-1,sizeof h);cin>>n>>m>>s;lyh(i,1,m){int a,b,c; cin>>a>>b>>c;add(a,b,c);}spfa();lyh(i,1,n){if(d[i] >= 0x3f3f3f) cout<<INT_MAX<<" ";//INT_MAX 是最大的int值也就是2^31-1else cout<<d[i]<<" ";	}
}

这篇关于图论单源最短路径——spfa的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---