搜狐2017实习生笔试题

本文主要是介绍搜狐2017实习生笔试题_概率问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、题目

工程师 M 发明了一种游戏：M 将一个小球随机放入完全相同的三个盒子中的某一个，玩家选中装有球的盒子即获胜；开始时 M 会让玩家选择一个盒子（选择任何一个获胜概率均为 1/3 ）;玩家做出选择后，M 会打开没有被选择的两个盒子中的一个空盒，此时 M 会询问玩家是否更改选择（可以坚持第一次选择，也可以选择另一个没有打开的盒子），下列叙述正确的有（）。

A. 改选后，玩家获胜的概率还是 1/3
B. 若不改选，玩家的获胜概率是 1/2
C. 无论怎么选择，获胜的概率都是 1/2
D. 坚持原来的选择获胜概率更高
E. 选择另一个没有被打开的盒子获胜概率更高
F. 获胜概率取决于随机因素（如小球的实际位置）

二、解题

一开始看到这个题的时候，本人毫不犹豫的选择了 A ，然后再仔细想了一下，不对啊，这题跟经典的三门问题很像，而且也要知道玩家第一次选择和是否更改选择的两个事件不是相互独立的，因此答案不是这个了，具体答案是什么呢？也欢迎读者留言写下自己的见解。

再说答案之前，先来了解一下经典的三门问题：

三门问题（ Monty Hall problem ）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目 Let’s Make a Deal 。问题名字来自该节目的主持人蒙提·霍尔（ Monty Hall ）。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机率？如果严格按照上述的条件，即主持人清楚地知道，哪扇门后是羊，那么答案是会。不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是2/3。
这个问题亦被叫做蒙提霍尔悖论：虽然该问题的答案在逻辑上并不自相矛盾，但十分违反直觉。这问题曾引起一阵热烈的讨论。

三门问题的解法：

三门问题一共有三种可能性：
(1)参赛者挑山羊一号，主持人挑山羊二号。转换将赢得汽车。
(2)参赛者挑山羊二号，主持人挑山羊一号。转换将赢得汽车。
(3)参赛者挑汽车，主持人挑羊一号。转换将失败和参赛者挑汽车，主持人挑羊二号。转换将失败，不会赢得汽车。

这里要注意了，第三种可能性的时候，概率还是 1/3 ，因为 1/3*1/2+1/3*1/2=1/3 ，所以上面的三种可能性都是相等的，都是 1/3 。从上面对的三种情况可以看到，如果参赛者重新选择另一扇门的话，得到汽车的概率就会变成 2/3 ，所以重新选择会更加的有利。一开始这个解释都不会让人信服的，因为此时我们还在纠结的是一开始分配的概率是1/3，然后去除了一个没有汽车的门后，两个选择，所以概率就是 1/2 ，还有一种纠结就是无论我们怎么选，三种情况，每次选择的概率都是 1/3 啊，当然，第二种选择很容易就给推翻了，因为主持人明确的去除了一个不会得到汽车的门，因此概率不会是 1/3 的。一开始我也在纠结这个，查了一下，就经典的解释就是把门的数量增多，比如：

现在摆在我们面前的有100扇门，只有其中一扇门后是汽车，而其他的99扇门后都是山羊。好了，你选择其中一扇门。自然，你选取汽车的概率只有1／100。

然后，知道汽车存放处的主持人一口气打开了99扇门中的98扇，其后面都是山羊。此时你可以坚持最初的选择，也可以改变选择。你是否应当改变选择?你是否还认为在你最初选择的门与其他99扇门中唯一没有打开的那扇门背后有汽车的概率是相同的?

事实是，如果你拒绝改变，你只有在一开始就选择了正确的门的情况下才能获取汽车，这个概率只有1％。在另外99％的情况下，你最初选择的是一个后面是山羊的门，而另外的98扇已经打开，你这时改变最初的选择就可以成功。所以，在99％的概率下，改变选择是正确的。

三门问题是一个理性选择和机遇博弈问题，是关于不完全信息博弈中如何正确理解概率的含义和概率变化的问题。可见这个问题我们仔细琢磨一下，还是可以做出正确的选择的。

显然这个还是不能太让人接受，因此写个 JAVA 程序来模拟一下这个场景：

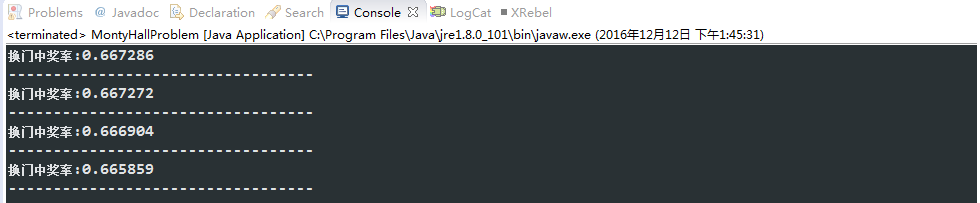
package com.liangdianshui;import java.util.Random;public class MontyHallProblem {public static void main(String[] args) {// 重复五次for (int i = 0; i < 4; i++) {montyHallProblem();System.out.println("----------------------------------");}}public static void montyHallProblem() {Random random = new Random(); // 这里不讨论Random为伪随机的问题int changeCount = 0;for (int i = 0; i < 1000000.0f; i++) { // 模拟一百万次// 假设有三个门int[] doors = new int[3];// 随机抽取一扇门 ,在门后放奖品int rIndex = random.nextInt(3);doors[rIndex] = 1;// 观众选的门号int randomSelect = random.nextInt(3);// 主持人从剩下的两扇门中排除一个while (true) {int randomDelete = random.nextInt(3);// 主持人不会打开参赛者已经选了的门（排除参赛者选择的门）if (randomDelete == randomSelect) {continue;}// 主持人不会打开有奖品的门（排除有奖品的门）if (doors[randomDelete] == 1) {continue;}for (int j = 0; j < 3; j++)// 换门{if (j == randomSelect)// 不换门（因为我们要得到的是换门的概率，因此把不换门的排除掉）continue;// 排除主持人打开了那个门（因为门已经打开，所以不能换，排除掉）if (j == randomDelete)continue;if (doors[j] == 1) {changeCount++;// 换了门后中奖的次数break;}}break;}}System.out.println("换门中奖率:" + changeCount / 1000000.0f);}}