宽度优先遍历--边权为1的最短路问题

本文主要是介绍宽度优先遍历--边权为1的最短路问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

💕"对相爱的人来说，对方的心意，才是最好的房子。"💕
作者：Lvzi
文章主要内容：宽度优先遍历–边权为1的最短路问题

一.定义

最短路问题是图论中非常经典的一种问题,其实就是通过代码找到两点之间的最优路径(往往是距离最短),最短路问题的解法很多,比如A*算法,迪杰斯特拉算法等等,本文介绍最短路问题中最简单的一种边权为1的最短路问题

所谓的边权,就是指两个地点之间的距离为1(如下图所示)

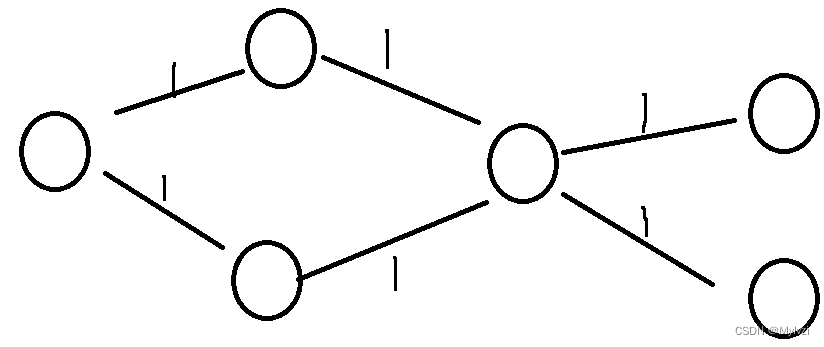
很明显,实际情况的道路更加复杂,两个地点之间的距离不能全是1,所以边权为1的最短路问题是比较特殊,简单的最短路问题

要记录整个过程的最短路,可以通过bfs来解决,选定一个地点,以这个地点为中心向外扩展(因为一个地点连接着很多的地点)

首先我们需要一个队列q来记录搜索的过程,需要一个hash来标记已经搜索过的路径

下面是leetcode上经典的三道题目

1.迷宫中离入口最近的距离

链接:迷宫问题

分析:

每次只能向周围走一步–距离为1–边权为1的最短路问题
剩下的代码就是bfs的经典代码

代码:

// 将本题转化为边权为1的的最短路问题
class Solution {int[] dx = { 1, -1, 0, 0 };int[] dy = { 0, 0, 1, -1 };int m, n;boolean[][] vis;public int nearestExit(char[][] maze, int[] e) {m = maze.length;n = maze[0].length;vis = new boolean[m][n];Queue<int[]> q = new LinkedList<>();q.add(e);vis[e[0]][e[1]] = true;int ret = 0;// bfswhile (!q.isEmpty()) {int sz = q.size();ret++;// 记录层数for (int j = 0; j < sz; j++) {// 下面的代码就是经典的bfs遍历的代码  多了一个边界情况的判断int[] t = q.poll();int a = t[0], b = t[1];vis[a][b] = true;for (int i = 0; i < 4; i++) {int x = a + dx[i], y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && maze[x][y] != '+') {if (x == 0 || x == m - 1 || y == 0 || y == n - 1)// 走到边界return ret;q.add(new int[] { x, y });vis[x][y] = true;}}}}return -1;// 没有找到出口}
}

总结:

• 其实大致的代码和bfs的代码很像,边权为1的最短路问题最大的特征就是一次只移动一步/只变化一个部分

2.最小基因变化

链接:最小基因变化

分析:

这道题目为什么也是边权为1的最短路问题呢?因为一次只能更改一个字符
代码的思路很好想,但是比较考验代码能力

代码:

// 转化为边权为1的最短路问题
// 也是比较经典的bfs问题
// start就是root根节点  他的孩子节点很多  一共 4 * 8 = 32个
// 之前是通过一个点向外扩展四个点  这四个点是通过两个向量dx,dy获得的
// 本题向外扩展时,去更改每一个字符即可
class Solution {public int minMutation(String startGene, String endGene, String[] bank) {Set<String> vis = new HashSet<>();// 用于标记已经搜索过的字符串（等价于vis）Set<String> hash = new HashSet<>();// 用于存储bank中的所有字符vis.add(startGene);for(String s : bank) hash.add(s);if(startGene.equals(endGene)) return 0;// 相等直接返回if(!hash.contains(endGene)) return -1;// end不是bank中的字符  不符合要求char[] change = {'A','C','G','T'};// 存储每次可以变化的字符Queue<String> q = new LinkedList<>();q.add(startGene);// 添加根节点int step = 0;// 记录层数while(!q.isEmpty()) {step++;int sz = q.size();// 获取当前层所有的元素个数while(sz-- > 0) {String t = q.poll();for(int i = 0; i < 8; i++) {for(int j = 0; j < 4; j++) {char[] tmp = t.toCharArray();tmp[i] = change[j];String next = new String(tmp);if(hash.contains(next) && !vis.contains(next)) {if(next.equals(endGene)) return step;// 等于最终的结果直接返回q.add(next);// 入队vis.add(next);// 标记为已经搜索}}}}}return -1;}
}

总结:

• 这里向外扩展的过程是通过字符更替实现的,之前的bfs问题中,遍历周围的元素是通过两个向量数组dx,dy实现的,本题在选定一个字符串之后,向外扩展的方式很多(子节点很多),一共8个字符,每一个字符都有4中更换方式,也就是一个字符串就有32个联通区域(子节点)

3.单词接龙

链接:单词接龙

分析:

和最小基因变化类似

代码:

// 本题的思路和--最小基因变化--的解法类似
// 这里的change需要遍历32个英文字母
// 边权为1的最短路问题的最短路的长度是通过长度来体现的
// 为什么是边权为1的最短路问题呢?一次只修改一个位置--等价于距离为1--边权为1
class Solution {public int ladderLength(String beginWord, String endWord, List<String> wordList) {int m = beginWord.length();Set<String> vis = new HashSet<>();// 标记Set<String> hash = new HashSet<>();// 判断是否在list之中vis.add(beginWord);for(String s : wordList) hash.add(s);if(!hash.contains(endWord)) return 0;char[] change = new char[32];for(int i = 0; i < 32; i++) change[i] = (char)('a' + i);Queue<String> q = new LinkedList<>();q.add(beginWord);int step = 1;while(!q.isEmpty()) {// 每一次回到这里都表示进入到下一层int sz = q.size();step++;while(sz-- > 0) {String t = q.poll();for(int i = 0; i < m; i++) {for(int j = 0; j < 32; j++) {char[] tmp = t.toCharArray();tmp[i] = change[j];String next = new String(tmp);while(hash.contains(next) && !vis.contains(next)) {if(next.equals(endWord)) return step;q.add(next);vis.add(next);}}}}}return 0;}
}

4.为高尔夫比赛砍树

链接:为高尔夫比赛砍树

分析:

• 本题有一个硬性的要求砍树的时候必须按照从矮到高的顺序砍,所以我们需要预先知道砍树的具体顺序,这其实是一个排序的过程,创建一个集合,存储所有树(>1)的下标,再根据树高去给这些下标排序(需要用到Collections.sort())

• 知道顺序之后就开始砍树,题目要求的是最短砍树的路径,细分到每一步其实就是求相邻高度两棵树之间的最短距离,且周围有障碍物,有没有发现很熟悉?对了,这就是迷宫问题么,本题其实就是多次迷宫问题

代码:

// 1.按照顺序砍树
// 2.计算两点的最短距离class Solution {int m, n;boolean[][] vis;// 标记搜索路径int[] dx = { 1, -1, 0, 0 };int[] dy = { 0, 0, 1, -1 };public int cutOffTree(List<List<Integer>> f) {m = f.size();n = f.get(0).size();List<int[]> order = new ArrayList<>();for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (f.get(i).get(j) > 1)order.add(new int[] { i, j });// 将所有的树添加进order之中}}// 根据下标对应的值排序Collections.sort(order, (a, b) -> {return f.get(a[0]).get(a[1]) - f.get(b[0]).get(b[1]);});int ret = 0;// 返回结果int bx = 0, by = 0;// 起始位置for (int[] tree : order) {// 遍历每一个树int ex = tree[0], ey = tree[1];// 终止位置int step = bfs(f, bx, by, ex, ey);// 针对每两棵树之间完成一次迷宫问题(带障碍物的最短路问题)if (step == -1)return -1;ret += step;bx = ex;by = ey;// 更新下一个起始位置}return ret;}// 下面就是迷宫问题的代码private int bfs(List<List<Integer>> f, int bx, int by, int ex, int ey) {if (bx == ex && by == ey)// 迷宫问题只有一次,但是本题要做多次迷宫问题,走到最后一棵树就要停下return 0;// 处理边界位置 走到最后一棵树了 步数为0vis = new boolean[m][n];Queue<int[]> q = new LinkedList<>();q.add(new int[] { bx, by });vis[bx][by] = true;int step = 0;while (!q.isEmpty()) {step++;int sz = q.size();while (sz-- > 0) {int[] t = q.poll();int a = t[0], b = t[1];for (int i = 0; i < 4; i++) {int x = a + dx[i], y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && f.get(x).get(y) != 0) {if (x == ex && y == ey)return step;q.add(new int[] { x, y });vis[x][y] = true;}}}}return -1;}
}

这篇关于宽度优先遍历--边权为1的最短路问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---