本文主要是介绍Arima相关概念,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
https://www.cnblogs.com/bradleon/p/6832867.html
https://www.cnblogs.com/bradleon/p/6827109.html
平稳性:就是要求经由样本时间序列所得到的拟合曲线在未来的一段期间内仍能顺着现有的形态“惯性”地延续下去。平稳性要求序列的均值和方差不发生明显变化
严平稳:严平稳表示的分布不随时间的改变而改变。如:白噪声(正态),无论怎么取,都是期望为0,方差为1
弱平稳:期望与相关系数(依赖性)不变,未来某时刻的t的值Xt就要依赖于它的过去信息,所以需要依赖性
差分法:时间序列在t与t-1时刻的差值
差分(d):现在数列=现时刻数值-前一时刻数值
也就是本时刻与前一时刻的差值作为新的数列,可以让数列 更加平稳,
数据.diff(1):1代表与前一时刻的差值,2代表与倒数第二个数的差值。
做一次.diff(1),就是一阶差分,再在一阶差分上做一次.diff(1),就是二阶差分。
1 自回归模型(AR)
描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测,自回归模型必须满足平稳性的。
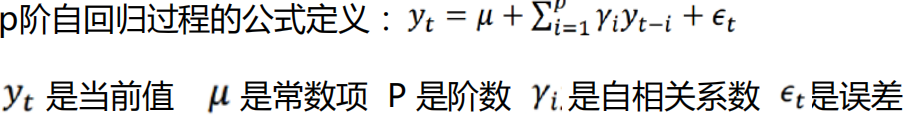
自回归(AR),就是指当前值只与历史值有关
p阶自回归,指当前值与前p个值有关
求常数u与自回归系数ri
自回归模型的限制
(1)自回归模型是用自身的数据来进行预测
必须具有平稳性
(2)必须具有自相关性,如果自相关系数(φi)小于0.5,则不宜采用
(3)自回归只适用于预测与自身前期相关的现象
2移动平均模型(MA)
移动平均模型关注的是自回归模型中的误差项的累加,移动平均法能有效地消除预测中的随机波动。
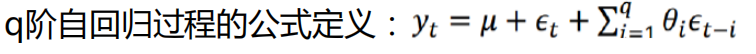
移动平均(MA),自回归中几个误差项累加
q为移动平均项数
q阶:与前q个误差有关
3自回归移动平均模型(ARMA)
自回归与移动平均的结合
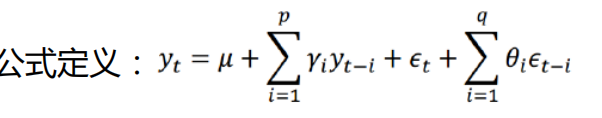
p,q指定,求解r,thta
4差分自回归移动平均模型 ARIMA(p,d,q)
AR是自回归, p为自回归项;
MA为移动平均,q为移动平均项数,
d为时间序列成为平稳时所做的差分次数
原理:将非平稳时间序列,转化为,平稳时间序列;然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型
5自相关函数ACF
有序的随机变量序列与其自身相比较
自相关函数反映了同一序列在不同时序的取值之间的相关性
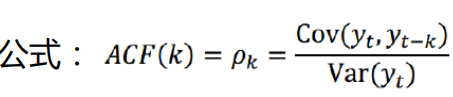
Pk的取值范围为[-1,1]
(1)在不同滞后阶数的相关性(一阶:Yt与Yt-1),滞后多少点
(2)虚线:置信区间 95%(100个点95个符合逻辑)
(3)横轴:p,0-20阶,滞后多少,也就是与前几个的关系
(4)阴影表示95%置信区间,点表示阶数
statsmodels 统计学习库
6 偏自相关函数(PACF)
对于一个平稳AR(p模型,求出滞后k自相关系数p(k)时,实际上得到并不是x(t)与x(t-k)之间单纯的相关关系。
x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的影响,而这k-1个随机变量又都和x(t-k)具有相关关系。
所以,自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响。
偏自相关函数,剔除了中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的干扰之后,x(t-k)对x(t)影响的相关程度。
ACF还包含了其他变量的影响。
PACF是严格这两个变量之间的相关性。
ACF包含了其他阶的影响
PCAF只包含这两阶的影响,更绝一些,把中间阶都剔除了
7 ARIMA(p,d,q)阶数确定:

截尾:落在置信区间内(95%的点都符合该规则)
AR(p看PACF
MA(q) 看ACF
ACF中第几个点落到阴影面积中,就为第几阶p
PACF中第几个点落到阴影面积中,就为第几阶q
ARIMA建模流程
(1)将序列平稳化(差分法确定d)
(2)p和q阶数确定(ACF,PACF)
(3)ARIMA(p,d,q)
模型选择:AIC、BIC、选择更简单的模型
AIC:参数与最终精度的权衡,越低越好
BIC:
画出热度图,越黑越小越好
qq图,若一条直线,则符合正态分布,越好
tsfresh库,自动提取时间序列特征
这篇关于Arima相关概念的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







