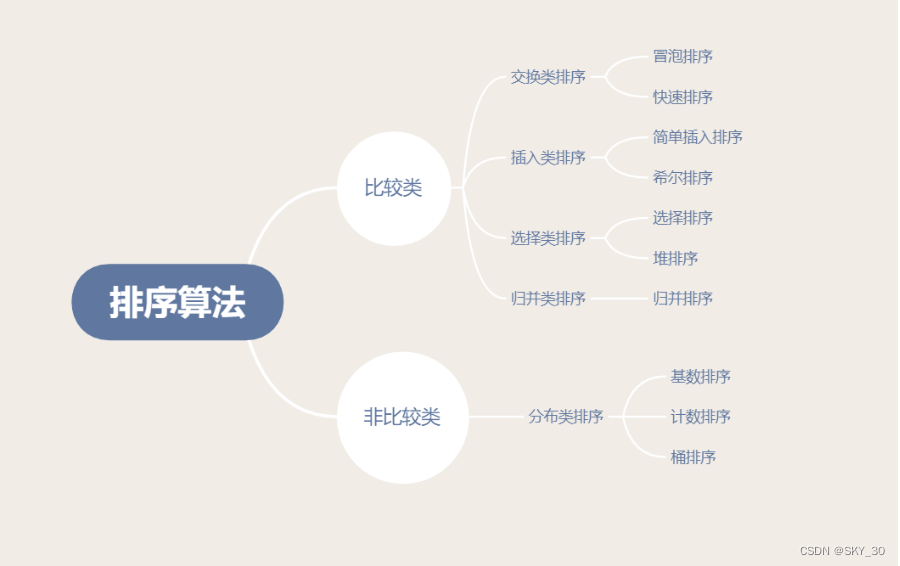
本文主要是介绍【java数据结构之八大排序(上)-直接插入排序,希尔排序,选择排序,堆排序,向下调整(大根堆,小根堆)等知识详解】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

🌈个人主页:努力学编程’
⛅个人推荐:基于java提供的ArrayList实现的扑克牌游戏 |C贪吃蛇详解
⚡学好数据结构,刷题刻不容缓:点击一起刷题
🌙心灵鸡汤:总有人要赢,为什么不能是我呢

hello,今天带大家学数据结构的一个非常重要的部分,排序!!!,回想博主的学习路程 ,好像真正学过的排序就是冒泡排序,其实数据结构里面有很多的排序的算法,针对不同的数据,我们往往采用不同的排序算法,合适的排序算法处理数据时可能会大大减少内存的消耗,和较短的运行时间。下面就带大家学习几种常见的排序算法。
🍪插入排序:
🍰直接插入排序:
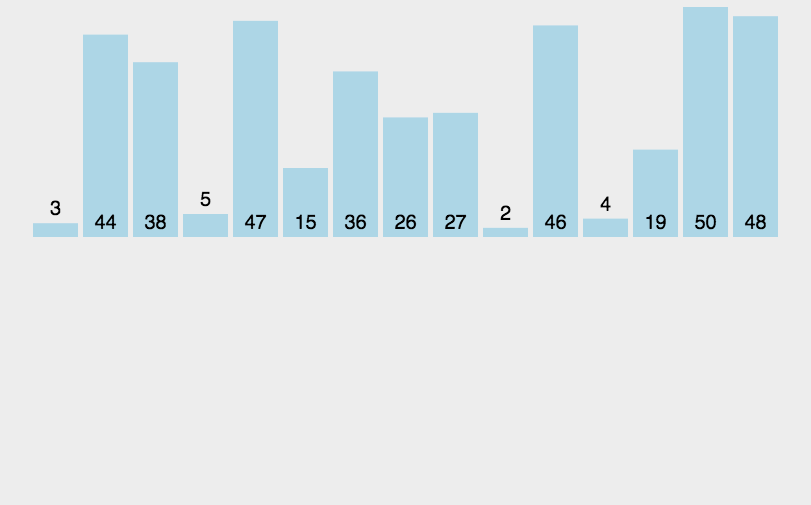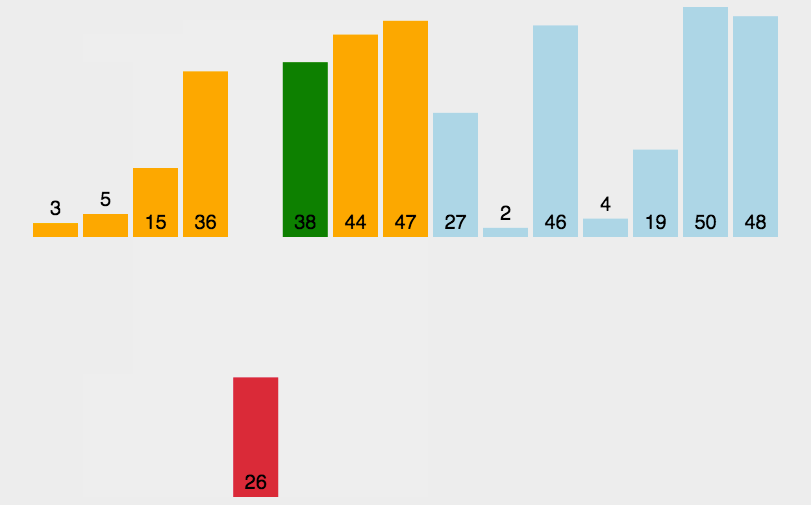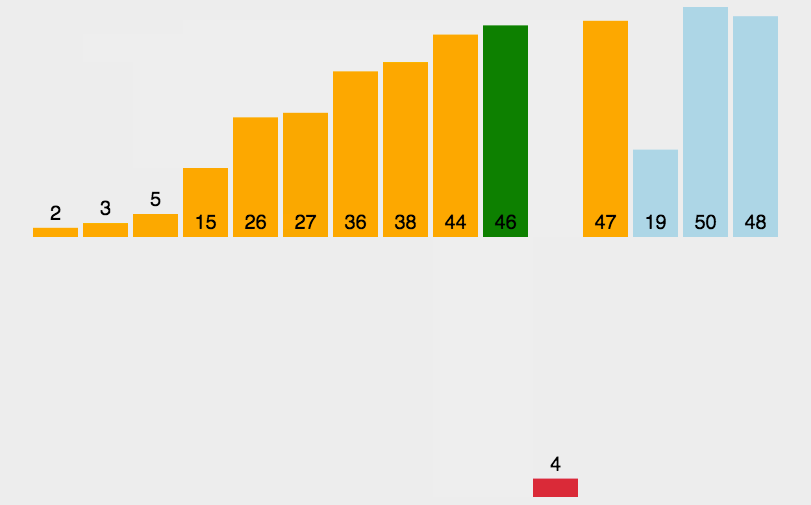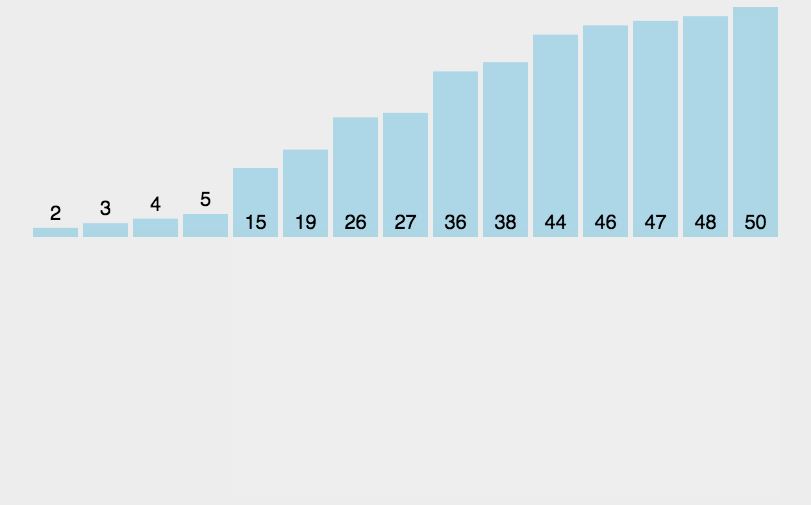
直接插入排序是一种简单直观的排序算法,将待排序的元素逐个插入到已经排序好的序列中的适当位置,从而得到一个新的、更长的有序序列。具体的实现呢,给大家列出来了:
1.初始状态:假设第一个元素已经是有序的序列。
遍历未排序部分:从第二个元素开始,逐个遍历未排序的元素。
插入操作:对于当前遍历到的元素,将其与已经排序好的序列中的元素依次比较,找到合适的位置插入。
2.移动元素:如果发现当前元素比已排序序列中的某个元素小(或大,取决于排序顺序),则将该元素后移一位,为当前元素腾出插入位置。
插入元素:找到合适的位置后,将当前元素插入到该位置。
重复:重复上述步骤,直到所有元素都被插入到有序序列中。
public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for (; j >= 0 ; j--) {if(array[j] > tmp) {array[j+1] = array[j];}else {array[j+1] = tmp;break;}}array[j+1] = tmp;}}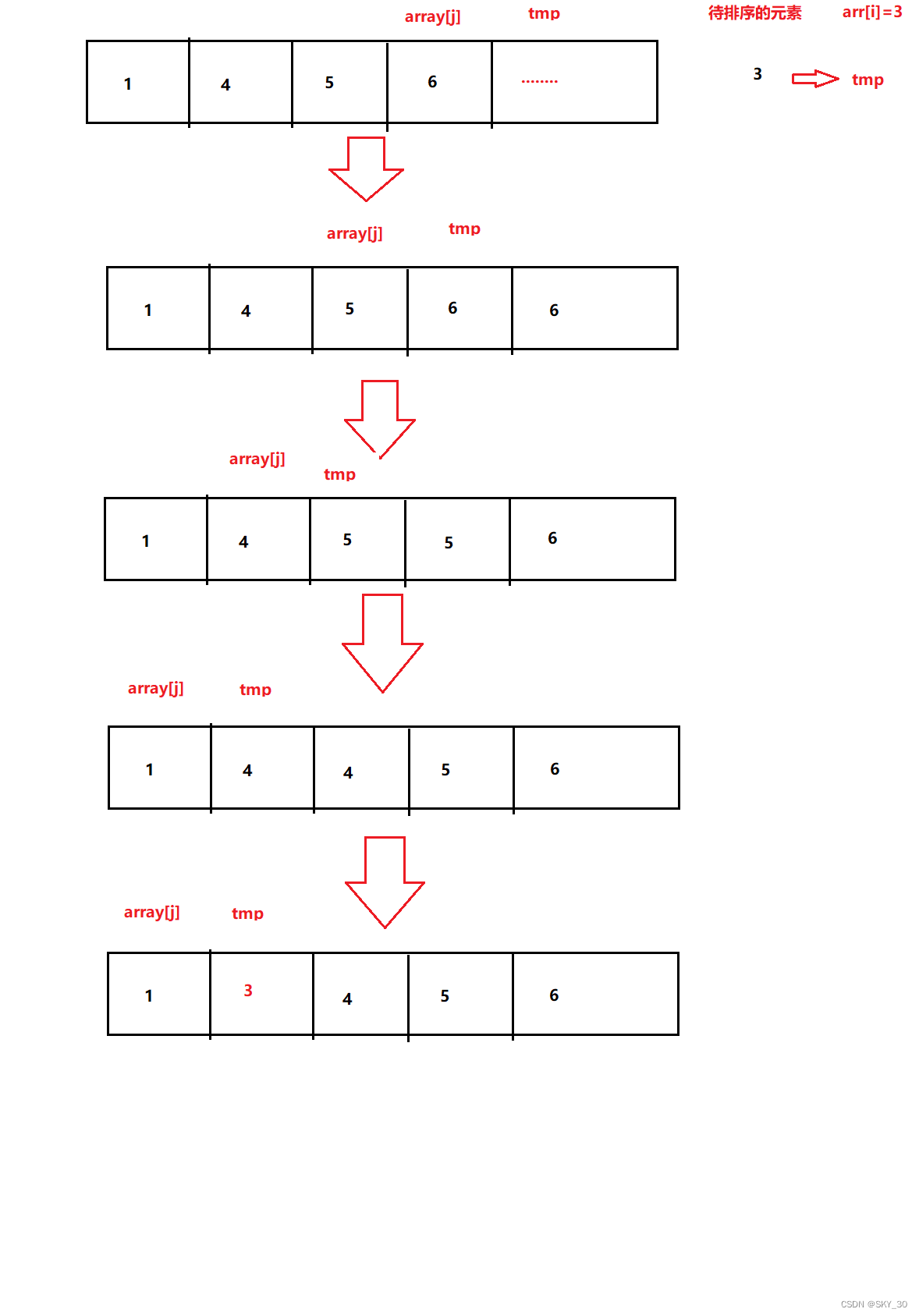
直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
🍰希尔排序
希尔排序又称为缩小增量排序,其本质是将所有的数据分成N组,每一组的元素对应的是从第一个开始,每N个的元素后的那个元素进行比较排序,依次对N组元素做同样的处理。
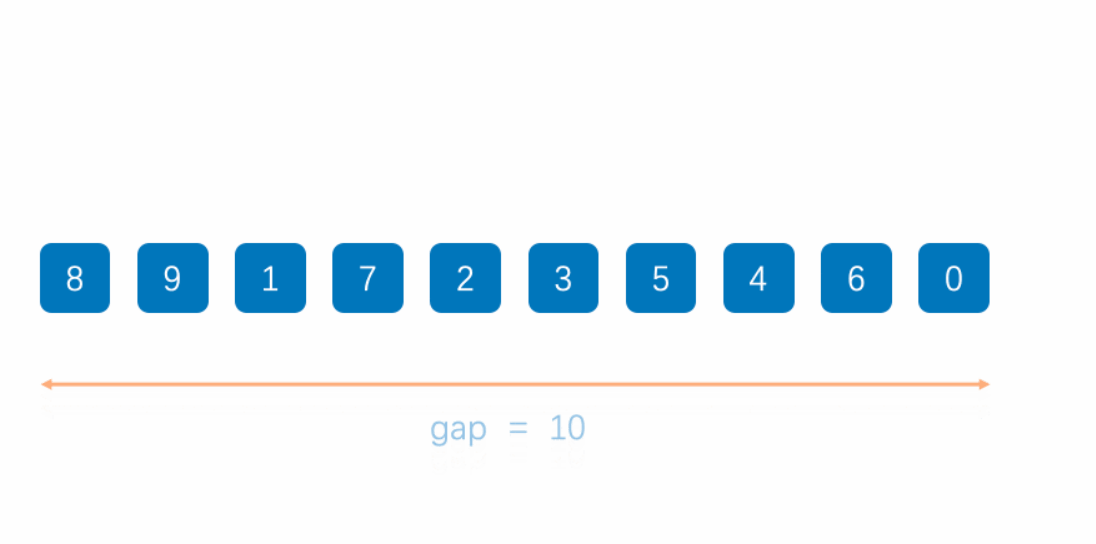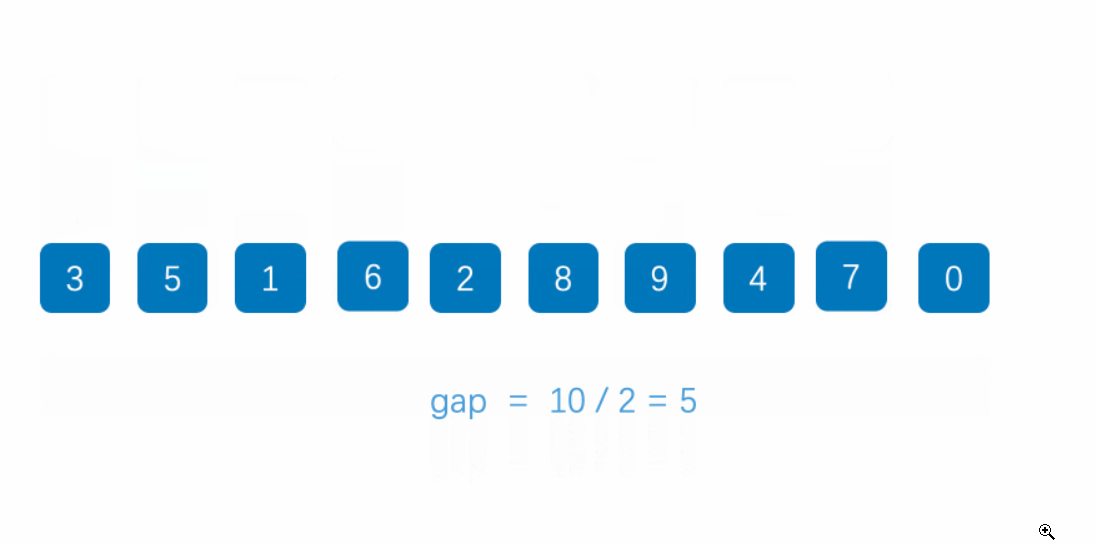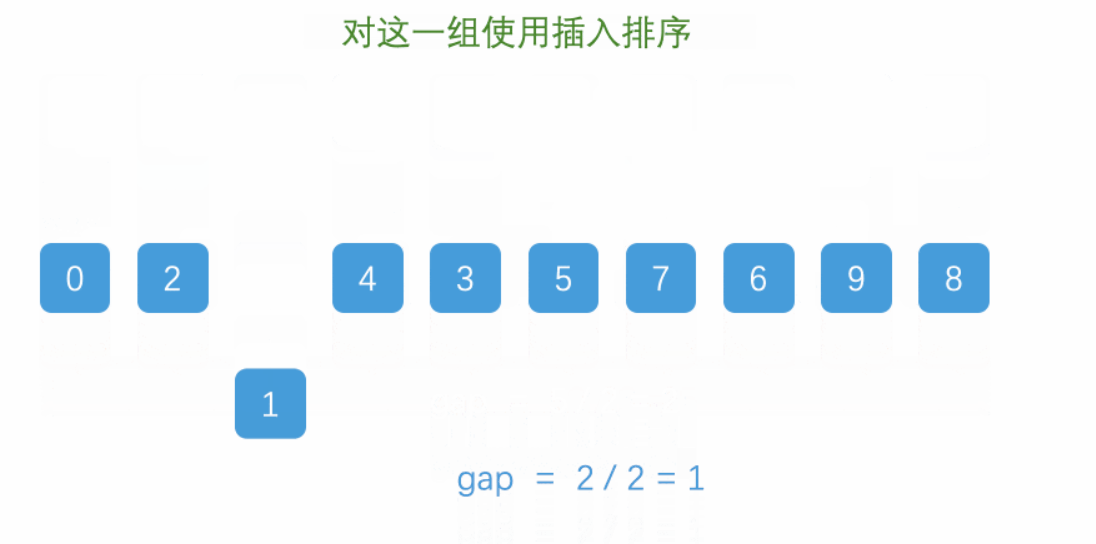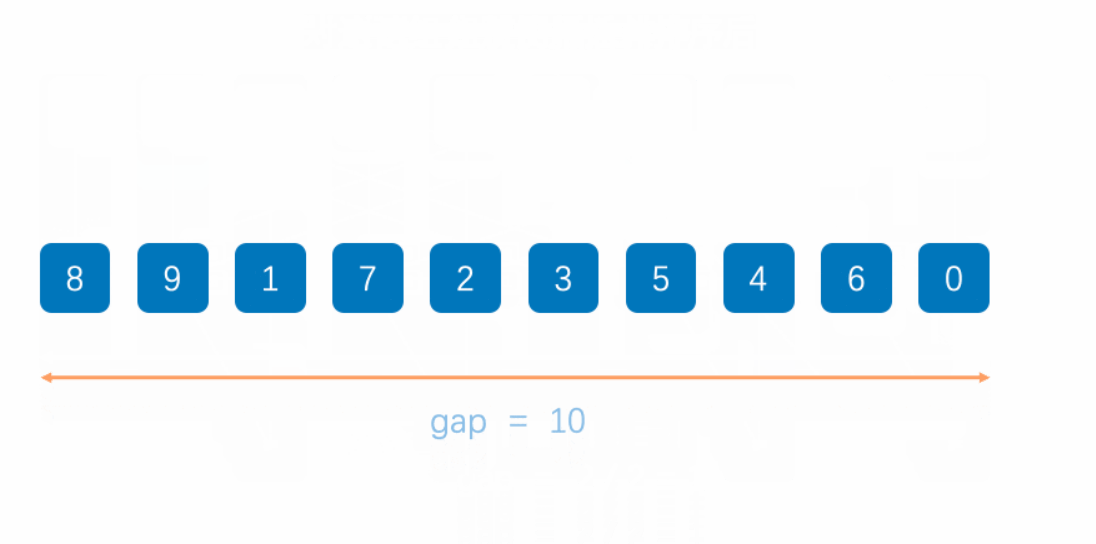
然后对数据重新分组,分为K组(K<N),然后重复上述操作对每组元素比较大小,直到分组为1,完成比较。
那么你可能会问,每次分组的时候,有什么依据吗,总不能想怎么分就怎么分吧,


我们这里为了方便期间,采用gap=[N/2]的处理方法,向下取整,将数据划分直到化为1为止。完成排序。由于不同的人可能采用不同的gap去划分数据,时间复杂度也就相应的可能会不同,所以希尔排序的时间复杂度不太好计算。
稳定性:不稳定
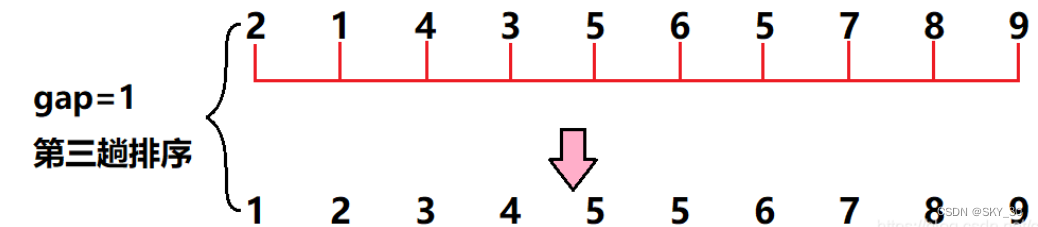
public static void shellSort(int[] array) {int gap = array.length;//nwhile (gap > 1) {gap = gap/3 + 1;shell(array,gap);}}/*** 每组进行插入排序* @param array* @param gap*/private static void shell(int[] array,int gap) {//i++ 交替进行插入排序for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i-gap;for (; j >= 0 ; j -= gap) {if(array[j] > tmp) {array[j+gap] = array[j];}else {break;}}array[j+gap] = tmp;}}private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}这里还是给大家具体演示一下,帮助大家理解。

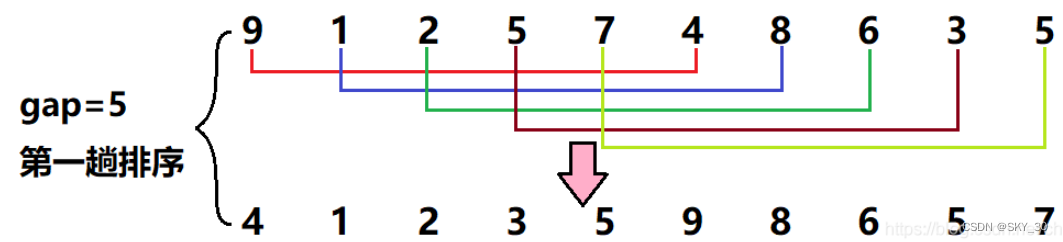
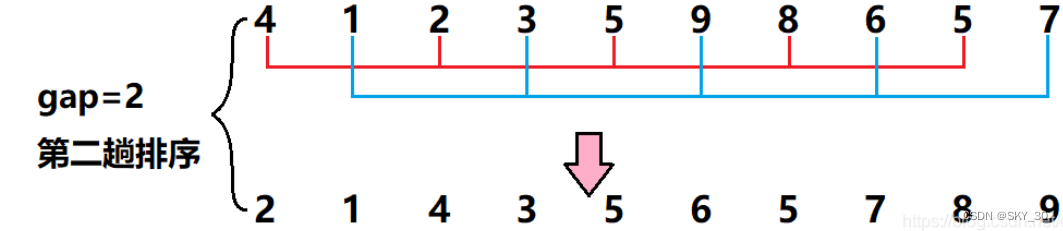
🍰选择排序
定义:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。

这里先给大家这个简单比较容易理解的版本:
public void selectSort(int[] array){for(int i=0;i<array.length;i++){int minindex=i;for(int j=i+1;j<array.length;j++){if(array[minindex]>array[j]){minindex=j;}}swap(array,minindex,i);}}public void swap(int[]array,int i,int j){int tmp=array[i];array[i]=array[j];array[j]=tmp;}
进行测试:
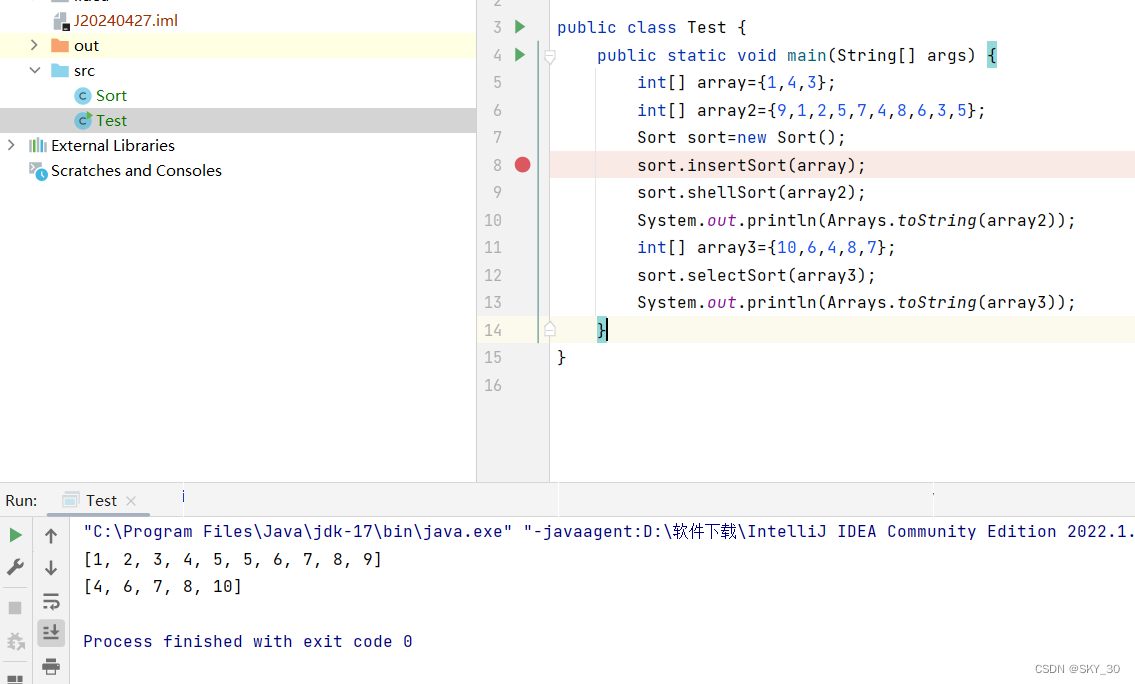
测试成功!!!
👋当然我们还有一种选择排序的另一种实现方法,我们每次遍历的时候,都选择两个元素,一个是这次遍历的最小元素,一个是最大的元素,分别放到数组的最左和最有端,然后就和上面的逻辑一样,继续遍历,更新最大值和最小值,遍历结束。
这里也把代码给大家,这端代码说起来简单,但是还是有很多的小细节的,大家细细品味一下。
public void selectSort2(int[] array) {int left=0;int right=array.length-1;while(left<right){int minIndex=left;int maxIndex=left;for(int i=left;i<right;i++){if(array[i]>array[maxIndex]) maxIndex=i;if(array[i]<array[minIndex]) minIndex=i;}swap(array,minIndex,left);//[10,6,4,8,7]这个例子大家按照代码的逻辑画个图//就会发现,排序失败原因是maxIndex==left我们在//第一次交换之后就会把maxIndex对应的值交换到minIndex中了//所以必须加一个判断if(left==maxIndex) maxIndex=minIndex;swap(array,maxIndex,right);left++;right--;}}
我把需要注意的地方注释出来了,希望大家还是可以自己在纸上画一下,这样会对整个过程有一个更加全面的认识。
1.直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
🍰堆排序
堆排序是我们所学的排序当中非常重要的一种排序,它实际上是建立在我们上一篇发布的文章优先级队列的基础上创建的一种排序方式,如果你对堆的概念还没有印象的话我建议你先去看看我的上一篇文章。
堆排序是建立在堆上的一种选择排序的算法,需要大家特别注意的是如果你要建立的是升序的序列的话。那么必须建立大根堆,降序的话,建立的是小根堆。
其实他的本事就是堆 里面的向下调整,我们上一篇文章也已经讲过了,那么他的过程到底是怎么样的,这里给大家演示一下。
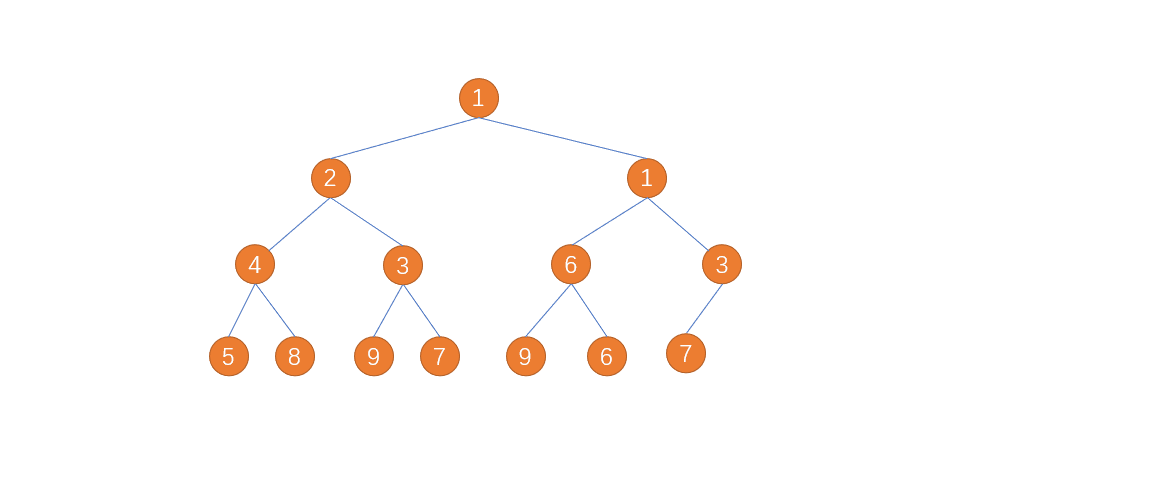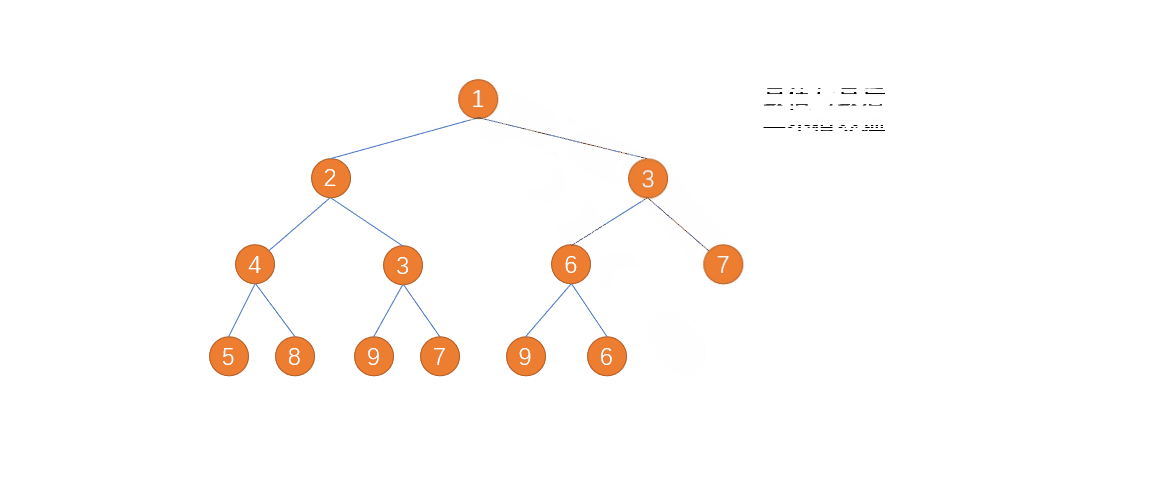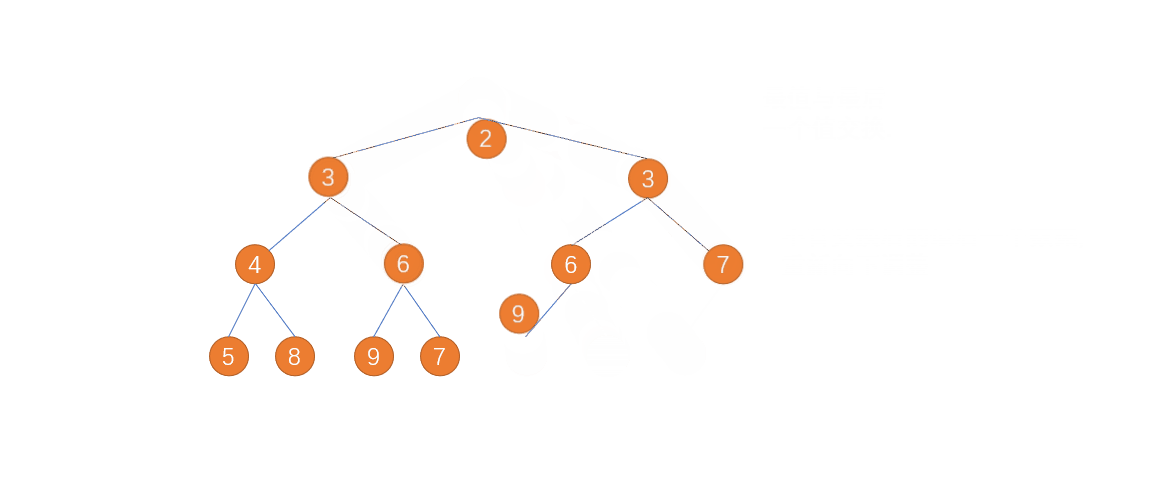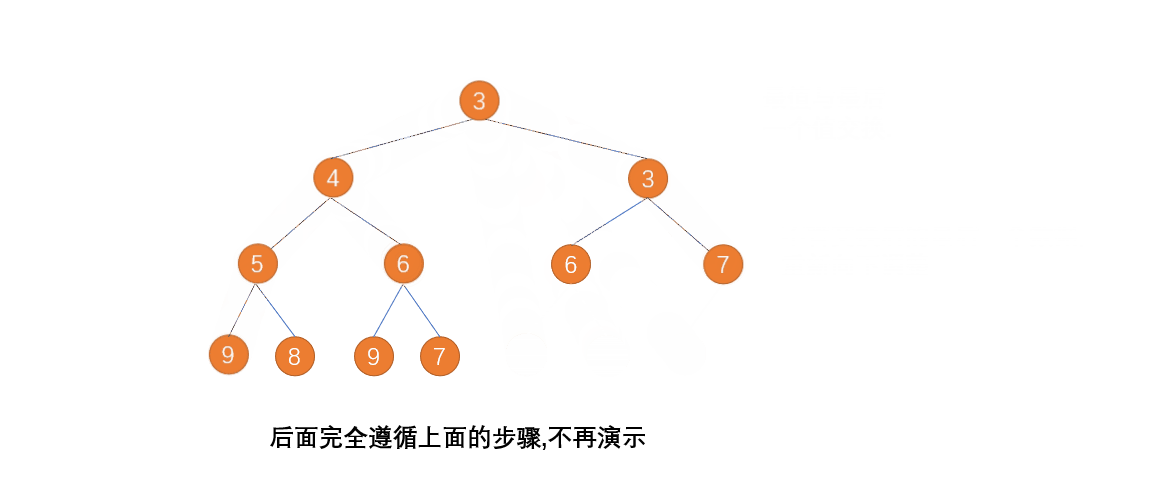
那我们第一步其实是创建一个大根堆,相信这个应该对大家来说不太难,我把代码给大家,里面有详细的注释,大家可以对照看看:
private void createBigHeap(int[] array){for(int parent=(array.length-1-1)/2;parent>0;parent--){//从最后一个叶子节点的父节点开始遍历,向下调整siftDown(parent,array,array.length);}}public void siftDown(int parent,int[] array,int end){int child=parent*2+1;while(child<end){if(child+1<end&&array[child]<array[child+1]){child++;}if(array[child]>array[parent]){swap(array,child,parent);//这里是因为把孩子节点与父节点交换之后可能有问题//所以对树的底层都要检查一下parent=child;child=parent*2+1;}else{break;}}}
接下来按照堆排序的定义,我们以此交换根节点和最后一个叶子节点,然后向下调整,直到结束,下面是完整的代码:
private void createBigHeap(int[] array){for(int parent=(array.length-1-1)/2;parent>0;parent--){//从最后一个叶子节点的父节点开始遍历,向下调整siftDown(parent,array,array.length);}}public void siftDown(int parent,int[] array,int end){int child=parent*2+1;while(child<end){if(child+1<end&&array[child]<array[child+1]){child++;}if(array[child]>array[parent]){swap(array,child,parent);//这里是因为把孩子节点与父节点交换之后可能有问题//所以对树的底层都要检查一下parent=child;child=parent*2+1;}else{break;}}}public void HeapSort(int[] array){createBigHeap(array);int end=array.length-1;while(end>=0){swap(array,end,0);siftDown(0,array,end);end--;}}
简单测试一下:
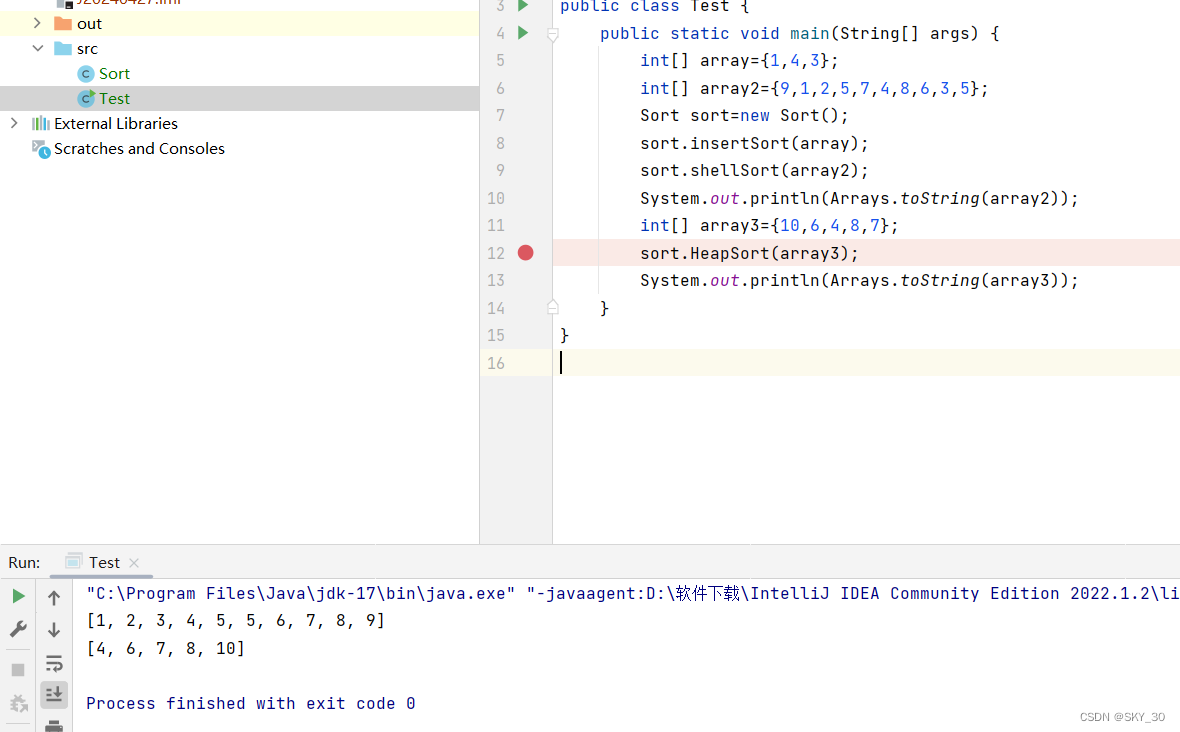
测试成功!!!
1.堆排序使用堆来选数,效率就高了很多。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
好了今天就带大家学习这么多了,下次带大家学习剩下的几种排序,觉得文章对你有帮助的话,一键三连,支持一下,同时欢迎评论区留下你宝贵的建议~~~
这篇关于【java数据结构之八大排序(上)-直接插入排序,希尔排序,选择排序,堆排序,向下调整(大根堆,小根堆)等知识详解】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!