本文主要是介绍【斐波那契】原来困扰多年的生兔子问题竟然能够轻松拿捏...万能公式法...,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上篇文章我们讲解了「矩阵快速幂」技巧,通过快速幂极大的优化了 斐波那契数列 的求解问题。并且通过分析知道了 系数矩阵 是解决问题的关键。
本文我们继续深化对于 系数矩阵 的求解,介绍一种通用方法,一举解决所有 斐波那契及变种类型 的问题。
提示: 先看 上篇文章 效果更佳哦~
生兔子问题
有一对兔子,从出生后第3个月起每个月都生一对兔子,小兔子长到第三个月后每个月又生一对兔子,假如兔子都不会死,问第 N 月有多少对兔子?

这道题不是典型的斐波那契数列么,递推公式为:

这和上道题目一模一样,根本不需要讲解。但是,我们对于本题进行一定的改编,增加点儿难度。
假设,现有一对成熟的兔子,新出生的兔子从出生的 第 4 个月 开始每月生一对兔子,问第 N 月有多少对兔子呢?
注意:
- 第一月已经有成熟的兔子了,所以从第二月开始就有新的兔子诞生了。
- 新出生的兔子三个月后才会生新的兔子。
通过分析不难发现:

因此,递推表达式为:

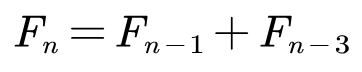
(如果这样不容易想出来,也可以自己动手列举列举,多写几项就能观察出规律啦)
关系推导
按照 上篇文章 的思路,我们做如下推导:
温馨提示:先看上篇文章更好理解哦~
将 三个相邻项 写成矩阵形式,由此可以得到关系式:

因此系数矩阵就得到了,后续的求解和上篇文章的简直一模一样了~
-----------------------桥豆麻袋---------------------
有小伙伴说了,这个系数矩阵不太会搞出来啊,那怎么办呢?有什么无脑办法么…哎,还真有!
这就要拿出我们初中就学过的万能的 待定系数法 了。
不就是一个系数矩阵嘛,我直接全设成未知数,一个一个解出来不就行了~
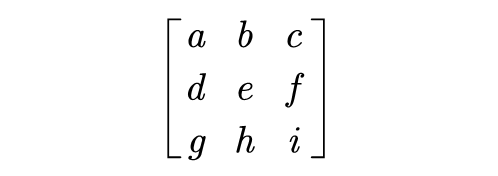
九个未知数,需要九个式子:


虽然看着麻烦,其实解起来也还行吧~哈哈哈,这样我们依然能够得到系数矩阵。
有了系数矩阵之后,就可以将第 n 项化简成只与前 3 项有关的式子。

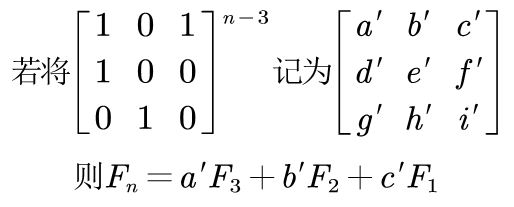
即系数矩阵的 n-3 次方的第一行与 F3, F2, F1 的内积和。
代码
public static int f(int n) {if (n < 1) {return 0;}if (n == 1 || n == 2 || n == 3) {return n;}int[][] base = { { 1, 0, 1 }, { 1, 0, 0 }, { 0, 1, 0 } };int[][] res = matrixPower(base, n - 3);return 3 * res[0][0] + 2 * res[0][1] + res[0][2];
}private static int[][] matrixPower(int[][] m, int p) {int[][] res = new int[m.length][m[0].length];for (int i = 0; i < res.length; i++) {res[i][i] = 1;}int[][] t = m;for (; p != 0; p >>= 1) {if ((p & 1) != 0) {res = produce(res, t);}t = produce(t, t);}return res;
}private static int[][] produce(int[][] a, int[][] b) {int n = a.length;int m = b[0].length;int k = a[0].length;int[][] ans = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {for (int c = 0; c < k; c++) {ans[i][j] += a[i][c] * b[c][j];}}}return ans;
}
只需在上篇文章代码中,将 f() 函数中初始边界条件、系数矩阵 以及 次方数和返回结果进行修改即可,另外两个函数无需做任何改变(具体细节可以参考 上篇文章 哦~)。
总结
通过本文的探讨,再次验证了 求解系数矩阵 就是解决此类斐波那契递推的关键。我们可以将结论进行适当推广:
当递推式是关于 F(n) 直到 F(n-i) 的,那么就可以将 i 项组合成一个矩阵,进行求解,此时需要构造一个 i*i 的系数矩阵,最终答案与 其 n-i 次方 和 前 i 项已知项的内积 有关。

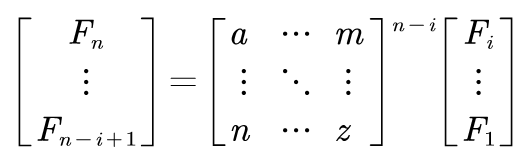
学习到这里,我们就得到了 斐波那契类型题 的 万能解法 了,稍微有点难度哦 ~~~ 点赞、转发让你的小伙伴们一起来学吧!!!
~ 点赞 ~ 关注 ~ 星标 ~ 不迷路 ~!!!
关注回复「ACM紫书」获取 ACM 算法书籍~
这篇关于【斐波那契】原来困扰多年的生兔子问题竟然能够轻松拿捏...万能公式法...的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







