matlab新手快速上手6（引力搜索算法）

2024-04-26 04:36
文章标签 matlab 快速 新手 上手 搜索算法 引力

本文主要是介绍matlab新手快速上手6（引力搜索算法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

        本文根据一个较为简单的matlab引力搜索算法框架详细分析蚁群算法的实现过程，对matlab新手友好，源码在文末给出。

引力搜索算法简介：

        引力搜索算法是一种启发式优化算法，最初于2009年由伊朗的Esmat Rashedi、Hossein Nezamabadi-pour和Saeid Saryazdi提出。这种算法灵感来源于引力的物理现象，其中个体之间的相互吸引力和排斥力决定了它们的运动轨迹，进而影响到最终的优化结果。

        这个算法的核心思想是模拟物体之间的引力和排斥力，以在解空间中搜索最优解。具体来说，每个解（个体）都被视为具有质量的物体，它们之间的相互作用由引力和排斥力来描述。通过计算每个解受到的引力和排斥力，可以更新它们的位置，以期望获得更优的解。

引力搜索算法的一般步骤如下：

  1. 初始化：随机生成初始解（个体）的位置。
  2. 计算适应度：计算每个解的适应度，也就是目标函数的值。
  3. 计算引力和排斥力：根据每个解之间的距离和适应度，计算相互之间的引力和排斥力。
  4. 更新位置：根据引力和排斥力的作用，更新每个解的位置。
  5. 重复迭代：重复执行步骤2到步骤4，直到达到终止条件（如达到最大迭代次数）。
  6. 输出结果：输出最优解或者最优解对应的适应度值。

        引力搜索算法的性能取决于参数的选择、种群大小和迭代次数等因素。这种算法适用于解决各种优化问题，包括连续型和离散型优化问题。

开始编程：

参数与子函数定义：

%============================== 引力搜索算法 ==============================
function GSA
%--------------------------------- 共性参数 -------------------------------
NP=30;                             %种群规模
D=10;                              %变量个数
Max_N=1000;                        %限定代数
G0=100;                            %引力常数
alpha=20;                          %引力常数
K0=NP;                             %更新常数
K1=1;                              %更新常数
%--------------------------------- 个性参数 -------------------------------
MinX=-30; MaxX=30;
%-------------------------------- 设置随机数 -------------------------------
rand('state',round(sum(100*clock)));
%---------------------------------- 初始化 ---------------------------------
X=MinX+(MaxX-MinX)*rand(NP,D);
V=zeros(NP,D);
%子函数（目标函数）
function fun=ackley(X)
fun=20+exp(1)-20*exp(-0.2*(sum(X.^2)/length(X))^0.5)...-exp(sum(cos(2*pi*X))/length(X));

参数定义：

        与前几章相同，NP代表天体个数，D代表解的维度。这里rand('state',round(sum(100*clock)));这行代码表示设置随机数种子，以确保每次运行程序时生成的随机数序列是不同的。

        初始化，生成X矩阵，矩阵维度为NP行D列，元素值为(MinX,MaxX)之间的随机值。V矩阵为NP行D列的元素全为0的矩阵。

子函数（目标函数）：

数学公式：

f(x_1, x_2, \ldots, x_n) = 20 + e - 20 \cdot e^{-0.2 \sqrt{\frac{1}{n} \sum_{i=1}^{n} x_i^2}} - e^{\frac{1}{n} \sum_{i=1}^{n} \cos(2\pi x_i)}

函数性质：

        由公式可知，此函数有多个极小值点，但最小值点在原点处，也就是当x(i)都为0时函数最小，为0。 此算法的目标是找到函数的全局最小值点，即找到使函数值最接近0的变量取值。

主函数：

%--------------------------------- 优化开始 -------------------------------
for gen=1:1:Max_NG=G0*exp(-alpha*gen/Max_N);K=round(K0+(K1-K0)*gen/Max_N);for i=1:1:NPF(i)=ackley(X(i,:));end[bestF,bestNo]=sort(F);best=min(F);worst=max(F);if best<worstm=(F-worst-eps)/(best-worst);elsem=ones(1,NP);endM=m/sum(m);
%-------开始引力搜索-------for i=1:1:NPfor k=1:1:DFt(i,k)=0;for j=1:1:Kif bestNo(j)~=itF(i,bestNo(j),k)=G*M(i)*M(bestNo(j))*...(X(bestNo(j),k)-X(i,k))/norm(X(i,:)-X(bestNo(j),:));Ft(i,k)=Ft(i,k)+rand*tF(i,bestNo(j),k);endendendendfor i=1:1:NPa(i,:)=Ft(i,:)/M(i);endV=rand(NP,D).*V+a;X=X+V;%----------------------------- 记录结果 -------------------------------GlobalMin_itr(gen)=best;if mod(gen,100)==0disp(['代数：',num2str(gen),'----最优：',num2str(best),...'----中值：',num2str(median(F)),'----均值：',...num2str(mean(F)),'----方差：',num2str(var(F))]);end
end
GlobalMin=best;
GlobalParams=X(bestNo(1),:);
plot([1:Max_N],GlobalMin_itr);
title('收敛曲线');

         第一个for循环表示循环迭代次数。

        G表示引力常数，公式为：G = G_0 \cdot e^{-\frac{alpha \cdot gen}{MaxN}}可知这是一个递减函数，也就是随着gen的增加，G值越小，也就是迭代次数越多，引力越小。

        K表示更新常数，公式为：K = \text{round}\left(K0 + \frac{(K1 - K0) \cdot gen}{MaxN}\right)，round函数表示四舍五入取整，这个公式表示通过线性插值的方式，将K在迭代过程中逐步从K0变为K1。也就是K0是初始更新常数，K1是最终的更新常数。

        接下来的for循环计算每个个体的适应度的值，存储在F对应的元素中。best存储最好的适应度的值，worst存储最差的，当最小值小于最差值时，计算归一化因子m对适应度的值进行归一化，也就是最好的个体对应的m为1，最差的对应为0。

        M为整体归一化过程，M中所有元素加起来为1，这个框架中的M的计算过程有点繁琐，可以直接采用M = ((1./F)/sum(1./F))来计算，效果是一样的，下面开始引力搜索，两个for循环遍历所有个体的所有元素，先让此元素为0。再次根据K更新常数进行遍历其他天体对此天体的引力影响。

        为什么根据K更新常数进行遍历呢，由上面可知，K是随着遍历次数增多而减少，线性地从NP减少到1，也就意味着在循环开始时，遍历所有个体对当前个体的引力，随着循环次数增多，K就能舍去最小的天体引力，也就是适应度最差的个体，在循环快到最后时，将只计算前几个引力强的个体对当前天体的影响。这就是K的作用。

        接下来是代码的核心部分：

        首先先了解一下引力公式：F = G\frac{Mm}{r^{2}}由引力公式可得出引力与M和m质量成正比，与r呈反比，因此下面实现通过引力更新位置的代码：

        if控制自身天体不会受自身引力影响，接下来就是计算当前天体受到前K个最优天体的引力影响后的方向与位置。tF矩阵中存储三个元素，表示第i个天体受到第bestNo(j)个天体在第k个维度的变化。G表示引力常数，G*M(i)*M(bestNo(j))表示对应上面引力公式的GMm，通过适应度表示质量，因此这个代码就实现了两个引力相互影响下的引力，这部分就实现了公式中的G\frac{Mm}{}部分。

        接下来实现r^{2}部分，由于引力与距离也有关系，距离越大引力越小那么继续编写代码

首先先理解norm函数，再matlab中，norm([3,4])将返回 5，做这个运算： \sqrt{3^2 + 4^2} = 5 。norm函数就是计算得出两个天体的欧几里得距离.

*(X(bestNo(j),k)-X(i,k))/norm(X(i,:)-X(bestNo(j),:));这里是难点 原代码中使用的是直接除以距离，虽然这样也可以，但是对比引力公式，这样这不便于理解，但是似乎效果更好，我在这里将源代码更改为此形式：

(X(bestNo(j),k)-X(i,k))/norm(X(i,:)-X(bestNo(j),:))^2;

来看此公式，/norm(X(i,:)-X(bestNo(j),:))^2;实现了/r^{2}这一部分，难点在于X(bestNo(j),k)-X(i,k)如何理解，为什么要乘以这个值呢？答案是控制引力方向。如下图所示，当不乘上这个值时，这样我们只计算出了具体的引力值大小F，但是我们需要的是将引力F映射到对应维度的力上，为了使F方向不改变，那么对应的F1和F2就要等比例缩放，因此再乘以X(bestNo(j),k)-X(i,k)这个差值就实现了将力分解到对应的维度上。

如图表示：二维状态下的力：

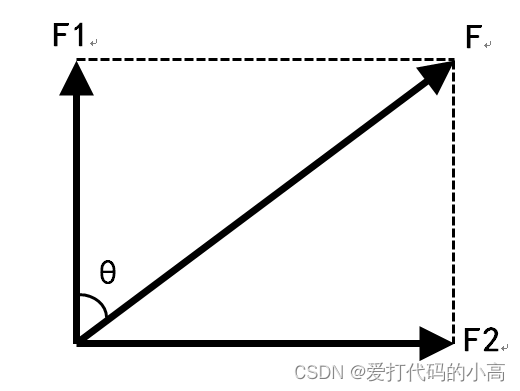
        继续通过Ft(i,k)更新第i个天体的第k个维度的受力，用当前维度的力加上tF，tF(i, bestNo(j), k)表示是第i个天体再第bestNo(j)个引力影响下第k维的力。再乘以随机值增加多样性，这样就得到了某个天体在前K个天体的引力影响下，在所有维度的的引力大小。

        继续看下面的代码，a(i,:)=Ft(i,:)/M(i)表示第i个天体的加速度，将时间设为单位时间，那么v = \frac{\Delta s}{\Delta t}a = \frac{\Delta v}{\Delta t}，就变为v = \Delta s，a = \Delta v,因此V=rand(NP,D).*V+a;就表示速度的变化，X=X+V;就表示经过距离的变化后的X。这样就实现了在引力作用下，一个单位时间的天体位置更新。后续就是结果处理，绘制图像等过程。

norm函数：

在 MATLAB 中，norm函数用于计算向量的范数。它可以计算向量的不同类型的范数，包括：

  1. 二范数（默认）：向量元素的平方和的平方根。
  2. 一范数：向量元素的绝对值之和。
  3. 无穷范数：向量元素的绝对值的最大值。

语法通常是norm(X)其中X是一个向量。例如,norm([3,4])将返回 5，因为这个向量的二范数是 \sqrt{3^2 + 4^2} = 5 ，norm([3,4,5]) = \sqrt{3^2 + 4^2 + 5^2} = 7.0711

源代码：

%============================== 引力搜索算法 ==============================%                  一个伊朗人2009年提出的一个非常漂亮的算法%============================== 引力搜索算法 ==============================
function GSA
%--------------------------------- 共性参数 -------------------------------
NP=30;                             %种群规模
D=10;                              %变量个数
Max_N=10000;                        %限定代数
G0=100;                            %引力常数
alpha=20;                          %引力常数
K0=NP;                             %更新常数
K1=1;                              %更新常数
%--------------------------------- 个性参数 -------------------------------
MinX=-30; MaxX=30;
%-------------------------------- 设置随机数 -------------------------------
rand('state',round(sum(100*clock)));
%rng(round(sum(100*clock)));
%---------------------------------- 初始化 ---------------------------------
X=MinX+(MaxX-MinX)*rand(NP,D);
V=zeros(NP,D);
%--------------------------------- 优化开始 -------------------------------
for gen=1:1:Max_NG=G0*exp(-alpha*gen/Max_N);K=round(K0+(K1-K0)*gen/Max_N);for i=1:1:NPF(i)=ackley(X(i,:));end[bestF,bestNo]=sort(F);best=min(F);worst=max(F);if best<worstm=(F-worst-eps)/(best-worst);%if gen == 10000%    disp(X(bestNo,:));%endelsem=ones(1,NP);end%M=m/sum(m);M = ((1./F)/sum(1./F));%-------开始引力搜索-------for i=1:1:NPfor k=1:1:DFt(i,k)=0;for j=1:1:Kif bestNo(j)~=itF(i,bestNo(j),k)=G*M(i)*M(bestNo(j))*...(X(bestNo(j),k)-X(i,k))/norm(X(i,:)-X(bestNo(j),:));%tF(i,bestNo(j),k)=G*M(i)*M(bestNo(j))*...%(X(bestNo(j),k)-X(i,k))/norm(X(i,:)-X(bestNo(j),:))^2;Ft(i,k)=Ft(i,k)+rand*tF(i,bestNo(j),k);endendendendfor i=1:1:NPa(i,:)=Ft(i,:)/M(i);endV=rand(NP,D).*V+a;X=X+V;%----------------------------- 记录结果 -------------------------------GlobalMin_itr(gen)=best;if mod(gen,100)==0disp(['代数：',num2str(gen),'----最优：',num2str(best),...'----中值：',num2str(median(F)),'----均值：',...num2str(mean(F)),'----方差：',num2str(var(F))]);end
end
GlobalMin=best;
GlobalParams=X(bestNo(1),:);
plot([1:Max_N],GlobalMin_itr);
title('收敛曲线');function fun=ackley(X)
fun=20+exp(1)-20*exp(-0.2*(sum(X.^2)/length(X))^0.5)...-exp(sum(cos(2*pi*X))/length(X));

结语：

        此章节为作者为准备考试所复习，暂时结束，大致的经典优化算法就是这些，后续遇到更好的智能优化算法还会继续更新。

这篇关于matlab新手快速上手6（引力搜索算法）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/936719。

相关文章

使用Python实现一个简易计算器的新手指南

使用Python实现一个简易计算器的新手指南

《使用Python实现一个简易计算器的新手指南》计算器是编程入门的经典项目,它涵盖了变量、输入输出、条件判断等核心编程概念,通过这个小项目,可以快速掌握Python的基础语法,并为后续更复杂的项目打下... 目录准备工作基础概念解析分步实现计算器第一步：获取用户输入第二步：实现基本运算第三步：显示计算结果进
阅读更多...
Python多线程实现大文件快速下载的代码实现

Python多线程实现大文件快速下载的代码实现

《Python多线程实现大文件快速下载的代码实现》在互联网时代,文件下载是日常操作之一,尤其是大文件,然而,网络条件不稳定或带宽有限时,下载速度会变得很慢,本文将介绍如何使用Python实现多线程下载... 目录引言一、多线程下载原理二、python实现多线程下载代码说明：三、实战案例四、注意事项五、总结引
阅读更多...
C#使用Spire.XLS快速生成多表格Excel文件

C#使用Spire.XLS快速生成多表格Excel文件

《C#使用Spire.XLS快速生成多表格Excel文件》在日常开发中,我们经常需要将业务数据导出为结构清晰的Excel文件,本文将手把手教你使用Spire.XLS这个强大的.NET组件,只需几行C#... 目录一、Spire.XLS核心优势清单1.1 性能碾压：从3秒到0.5秒的质变1.2 批量操作的优雅
阅读更多...
基于Python实现温度单位转换器(新手版)

基于Python实现温度单位转换器(新手版)

《基于Python实现温度单位转换器(新手版)》这篇文章主要为大家详细介绍了如何基于Python实现温度单位转换器,主要是将摄氏温度(C)和华氏温度(F)相互转换,下面小编就来和大家简单介绍一下吧... 目录为什么选择温度转换器作为第一个项目项目概述所需基础知识实现步骤详解1. 温度转换公式2. 用户输入处
阅读更多...
Mybatis-Plus 3.5.12 分页拦截器消失的问题及快速解决方法

Mybatis-Plus 3.5.12 分页拦截器消失的问题及快速解决方法

《Mybatis-Plus3.5.12分页拦截器消失的问题及快速解决方法》作为Java开发者,我们都爱用Mybatis-Plus简化CRUD操作,尤其是它的分页功能,几行代码就能搞定复杂的分页查询... 目录一、问题场景：分页拦截器突然 “失踪”二、问题根源：依赖拆分惹的祸三、解决办法：添加扩展依赖四、分页
阅读更多...
c++日志库log4cplus快速入门小结

c++日志库log4cplus快速入门小结

《c++日志库log4cplus快速入门小结》文章浏览阅读1.1w次，点赞9次，收藏44次。本文介绍Log4cplus，一种适用于C++的线程安全日志记录API，提供灵活的日志管理和配置控制。文章涵盖... 目录简介日志等级配置文件使用关于初始化使用示例总结参考资料简介log4j 用于Java，log4c
阅读更多...
使用Redis快速实现共享Session登录的详细步骤

使用Redis快速实现共享Session登录的详细步骤

《使用Redis快速实现共享Session登录的详细步骤》在Web开发中,Session通常用于存储用户的会话信息,允许用户在多个页面之间保持登录状态,Redis是一个开源的高性能键值数据库,广泛用于... 目录前言实现原理：步骤：使用Redis实现共享Session登录1. 引入Redis依赖2. 配置R
阅读更多...
Linux如何快速检查服务器的硬件配置和性能指标

Linux如何快速检查服务器的硬件配置和性能指标

《Linux如何快速检查服务器的硬件配置和性能指标》在运维和开发工作中,我们经常需要快速检查Linux服务器的硬件配置和性能指标,本文将以CentOS为例,介绍如何通过命令行快速获取这些关键信息,... 目录引言一、查询CPU核心数编程（几C？）1. 使用 nproc（最简单）2. 使用 lscpu（详细信
阅读更多...
一文详解如何在idea中快速搭建一个Spring Boot项目

一文详解如何在idea中快速搭建一个Spring Boot项目

《一文详解如何在idea中快速搭建一个SpringBoot项目》IntelliJIDEA作为Java开发者的‌首选IDE‌,深度集成SpringBoot支持,可一键生成项目骨架、智能配置依赖,这篇文... 目录前言1、创建项目名称2、勾选需要的依赖3、在setting中检查maven4、编写数据源5、开启热
阅读更多...
MybatisX快速生成增删改查的方法示例

MybatisX快速生成增删改查的方法示例

《MybatisX快速生成增删改查的方法示例》MybatisX是基于IDEA的MyBatis/MyBatis-Plus开发插件,本文主要介绍了MybatisX快速生成增删改查的方法示例,文中通过示例代... 目录1 安装2 基本功能2.1 XML跳转2.2 代码生成2.2.1 生成.xml中的sql语句头2
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2