本文主要是介绍动态规划——切割钢条问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、动态规划
动态规划算法通常用于解决最优化问题(寻求最优解)。其思想与分治法类似,将待求解的问题分成若干个子问题,先求出子问题,再根据子问题的解求出原来问题中的解,与分支法不同的是,在动态规划中,这些子问题的解是不相互独立的。
采用动态规划求解的问题通常有以下性质:
1.最优化原理:问题的最优解中包含的子问题的解也是最优的。
2.无后效性:即某阶段状态一旦确定,就不受该状态以后决策的影响,只与当前状态有关。
3.有重叠子问题:子问题之间是不相互独立的,一个子问题在下一阶段的决策中可能被多次用到。(通常减少不必要的重复操作)
二、钢条切割问题
给定一段长度为 n 的钢条和一个价格表 pi ,求钢条切割方案使得销售收益 rn 最大。
| 长度I | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 价格pi | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
案例:长度为 4 的钢条,如何切割使得销售额最高?
考虑两种情况:1.切割成4个长度为1的钢条,总收益是4;
2.切割成2个长度为2的钢条,总收益是10。
3.切割成1个长度为1和一个长度为3的钢条,总收益是9
4.切割成1个长度为4的钢条,总收益为9
法一(易理解)
对于求收益r[n]最大的切割方案(最优解)
1.不切割,收益为 pn
2.先将该钢条分为切为两根,则当该两根钢条的收益之和最大时(取最优解时),对应长度为n的钢条收益也最大,最优解的和就是当前情况的最优解,可以得出:
法二 (简单)
对于该求解方法可以改为一种相似但更简单的递归求解方法:
将钢条从左边切割下长度为 i 的一段,只对右边剩下的长度为 n-i 的一段继续进行切割(递归求解),对左边的一段不再进行切割。
关于此想法的理解:
将长度为n的钢条分解为左边开始一段,以及剩余部分继续分解的结果(通过递归)
或者理解为:对于一根长度为n钢条,总存在某种切割,会使得切出长度为 i 的钢条
此时公式为:
递归函数的伪代码为:
int get_best(int n)
{if(n<=0) return 0;int maxn=-1;for(int i=1;i<=n;i++)maxn=max(p[i]+get_best(n-i),maxn); // 通过递归求出最大//r[n]=maxn;return maxn;
}根据代码不难发现,在递归函数get_best中,会存在同一个变量反复递归的情况,从而引起时间的浪费,此时时间复杂度达到 O(2^n)
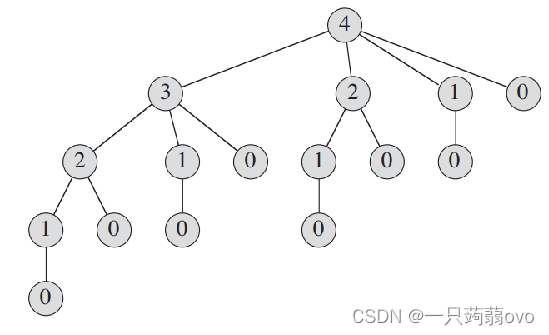
需要通过剪枝的方法避免重复的操作(自顶向下法)
int get_best(int n)
{if(n<=0) return 0;if(r[n]>0) return r[n]; // 若已经访问过,即找到r[n]的最优解时,直接返回int maxn=-1;for(int i=1;i<=n;i++)maxn=max(p[i]+get_best(n-i),maxn);r[n]=maxn;return maxn;
}此外,还可以通过自底向上的方法求出最优解,此时为递推操作,不需要递归
int get_best2(int n)
{for(int i=1;i<=n;i++){r[i]=p[i]; // 直接将 长度为 i的切割下 for(int j=1;j<i;j++)r[i]=max(r[i],p[j]+r[i-j]); //免去递归操作 }} 重构解
将最优解的切割方案求出
int get_best2(int n)
{for(int i=1;i<=n;i++){r[i]=p[i]; // 直接将 长度为 i的切割下 s[i]=i;for(int j=1;j<i;j++)if(r[i]<p[j]+r[i-j]) //免去递归操作 {r[i]=p[j]+r[i-j];s[i]=j; // 表示当长度为i时,将切割长度为j的钢条 ,剩余 i-j 已经求出最优解和切割方案了 }}int x=n;while(x>0){printf("%d ",s[x]);x-=s[x];}
}此过程只需在求解规模为 i 的子问题时将,第一段钢条的最优切割长度j保存在 s [ i ] 中
这篇关于动态规划——切割钢条问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






