利用MATLAB理解常见概率分布

本文主要是介绍利用MATLAB理解常见概率分布，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

二项分布

在概率论和统计学中，二项分布（英语：Binomial
distribution）是n个独立的是/非试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上，当n= 1时，二项分布就是伯努利分布。二项分布是显著性差异的二项试验的基础。

>> N=100;
>> p=0.5;
>> k=0:N;
>>pdf=binopdf(k,N,p);
>> cdf=binocdf(k,N,p);
>> h=plotyy(k,pdf,k,cdf)

binopdf(k,N,p)函数
表示事件A发生k次的概论
N为实验次数，p为发生概率
binocdf(k,N,p)函数
表示事件A发生次数不大于k次的概率
plotyy(k,pdf,k,cdf)函数
plot只有一个纵坐标，而plotyy有两个纵坐标（左右各一个），两个纵坐标标度有利于图形数据的对比分析

泊松分布

泊松分布是二项分布n很大而p很小时的一种极限形式 二项分布是说，已知某件事情发生的概率是p，那么做n次试验，事情发生的次数就服从于二项分布。
泊松分布是指某段连续的时间内某件事情发生的次数，而且“某件事情”发生所用的时间是可以忽略的。
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。

维基百科：

若$X$服从参数为$\lambda$ 的泊松分布，记为$X\sim \pi (\lambda )X\sim \pi (\lambda )$，或记为$X\sim P(\lambda )X\sim P(\lambda )$.
1、服从泊松分布的随机变量，其数学期望与方差相等，同为参数{\displaystyle \lambda }\lambda : {\displaystyle E(X)=V(X)=\lambda }{\displaystyle E(X)=V(X)=\lambda }

2、两个独立且服从泊松分布的随机变量，其和仍然服从泊松分布。更精确地说，若$X\sim Poisson({\lambda }_1)$$X\sim Poisson({\lambda }_1)$且$Y\sim Poisson({\lambda }_2)$$Y\sim Poisson({\lambda }_2)$，则$X+Y\sim Poisson({\lambda }_1+{\lambda }_2)$$X+Y\sim Poisson({\lambda }_1+{\lambda }_2)$。

在二项分布的伯努利试验中，如果试验次数n很大，二项分布的概率p很小，且乘积λ= np比较适中，则事件出现的次数的概率可以用泊松分布来逼近。事实上，二项分布可以看作泊松分布在离散时间上的对应物。

x=0:200;
px=poisspdf(x,100); 
plot(x,px)

表示已经观察到事物平均发生lambda次的条件下，实际发生X次的概率

是不是和二项分布很像？

均匀分布

在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U（a，b）。

均匀分布的期望：均匀分布的期望是取值区间[a,b]的中点(a+b)/2。
均匀分布的方差：var(x)=E[X²]-(E[X])²
var(x)=E[X²]-(E[X])²=1/3(a²+ab+ b²)-1/4(a+b)²=1/12(a²-2ab+ b²)=1/12(a-b)²

 x = rand(1000);
hist(x);
Ex = mean(x);
v = var(x);

指数分布

用一个知乎的简单解释：
（馒头那个太长就不抄了

可以用等公交车作为例子：
某个公交站台一个小时内出现了的公交车的数量 就用泊松分布来表示
某个公交站台任意两辆公交车出现的间隔时间 就用指数分布来表示

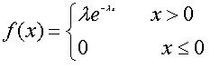
其中λ > 0是分布的一个参数，常被称为率参数（rate parameter）。即每单位时间内发生某事件的次数。指数分布的区间是[0,∞)。 如果一个随机变量X呈指数分布，则可以写作：X~ E（λ）。 [1]

>> x=0:0.2:20;
>> y1=exppdf(x,3);
y2=exppdf(x,5);
>> hold on;
plot(x,y1,'r');
plot(x,y2,'b');
>> 

hold on 和hold off 函数：
保留/删除上面的图像
exppdf()函数
产生指数分布的概率密度函数

我也来用馒头做一个解释（
比如x=0:0.2:20;
y1=exppdf(x,3);
已经观察到“馒头卖出”事件平均发生lambda次的条件下，实际发生X次的概率

这篇关于利用MATLAB理解常见概率分布的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---