【双曲几何】圆盘上的三角形概念

本文主要是介绍【双曲几何】圆盘上的三角形概念，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、说明

本文对双曲空间的三角形进行分析，本篇首先给出，参考圆内外的点映射，进而说明三角形形状的反演映射关系。进而给出正交三角图和射影中心的概念。我i们常常提到庞加莱盘的概念，但是深入探讨的时候，发现许多常识的不足，本篇也只是一些基本常识。基本概念而已。

二、对偶三角形概念

2.1 反演关系

本文中提到的测地线是外部测地线，它们是通过相对于单位半径地平圆的边界反演内部测地线而获得的，该地平线充当反演的镜子。这可以在数学上表达为 OA 乘以 OB 等于 OT 的平方，这相当于圆的性质，即与圆相交的两条线段的乘积等于切线或其幂的平方。
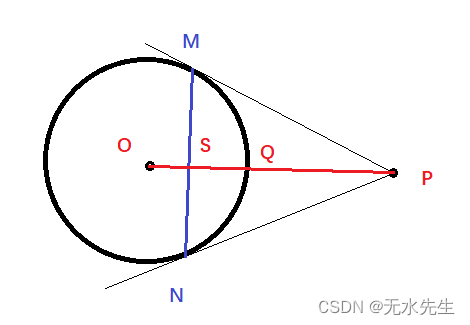
在这里插入图片描述
在图中， $r^2=OQ^2=OS\times OP$ 这可以轻易证明。
因此，在圆外的广大区域内任意点P都可以反演到圆内S点。因此，P和S构成反演关系。其中，S是P的极线MN的中点。
结论：反演将无限平面空间的任意点，变换成圆盘空间的一点，反之亦然。这是庞加莱盘的构建基础。

2.2 对偶关系

上图提起反演，我们立刻想到的是单位圆的极点和极线的关系：
参考圆：以O为圆心的圆C（可以是单位圆）。
极点：在C外的任意点P。
极线：MN是P点的对偶线，P是MN的对偶点。

2.3 找出三角形的对偶三角形

何为对偶三角形，我们这里给出一个三角形 $\overline{a_1a_2a_3}$ ，置于基础圆盘附近，下面将一步一步说明，其对偶三角形的概念。

三角形图元：（triangle） $\overline{a_1a_2a_3}$
相关三个边：（associated trilateral） $\overline{L_1L_2L_3}$
对偶三个边：（dual trilateral） $\overline{A_1A_2A_3}$
对偶三角形：（dual triangle） $\overline{l_1l_2l_3}$
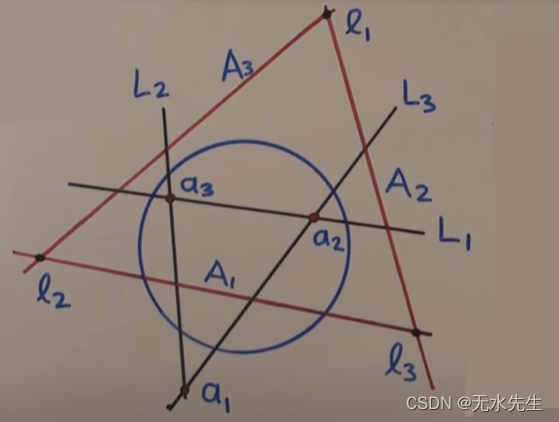
在这里插入图片描述
如图所示：其中：
$\overline{a_1a_2}=L_3$ ,
$\overline{a_1a_3}=L_2$ ,
$\overline{a_2a_3}=L_1$
以上标注了三条边。
做 $\overline{a_1a_2a_3}$ 的对偶极线：构成对偶三个边：（dual trilateral）
$\overline{A_1A_2A_3}$
通过对偶边，获得对偶顶点，构成对偶三角形
$\overline{A_1A_2}=l_3$
$\overline{A_2A_3}=l_1$
$\overline{A_1A_3}=l_2$
至此，对偶三角形被画出。
一句话，三角形顶点的极线构成对偶三角形。

三、正交三角形概念

3.1 通过对偶三角形，找到垂心

在图2中，找到三角形 $\overline{a_1a_2a_3}$ 的对偶三角形 $\overline{l_1l_2l_3}$
我们在图2的基础上，连接 $\overline{a_1l_1}$ , $\overline{a_2l_2}$ ， $\overline{a_3l_3}$ ，此三条线交于h点，h点叫做三角形 $\overline{a_1a_2a_3}$ 的垂心。
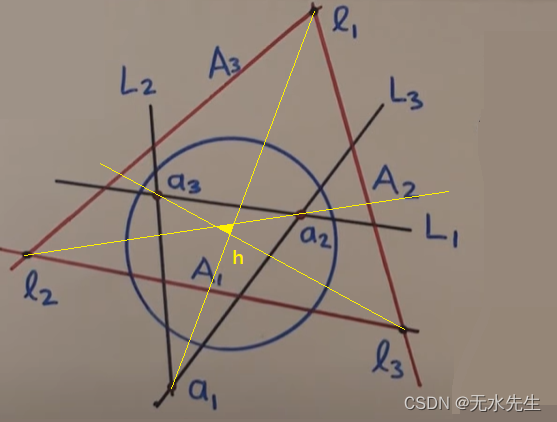
在这里插入图片描述

3.2 正交三角形的概念

我们在图2的基础上，连接 $\overline{a_1l_1}$ , $\overline{a_2l_2}$ ， $\overline{a_3l_3}$ ，此三条线是三角形 $\overline{a_1a_2a_3}$ 的垂线，分别交 $L_1$ 于 $b_1$ ，交 $L_2$ 于 $b_2$ ，交 $L_3$ 于 $b_3$ ，其中 $\overline{b_1b_2b_3}$ 构成正交三角形。
在这里插入图片描述

3.3 中心射影点的概念

因为上图太过稠密，这里更换一个图形继续说明。
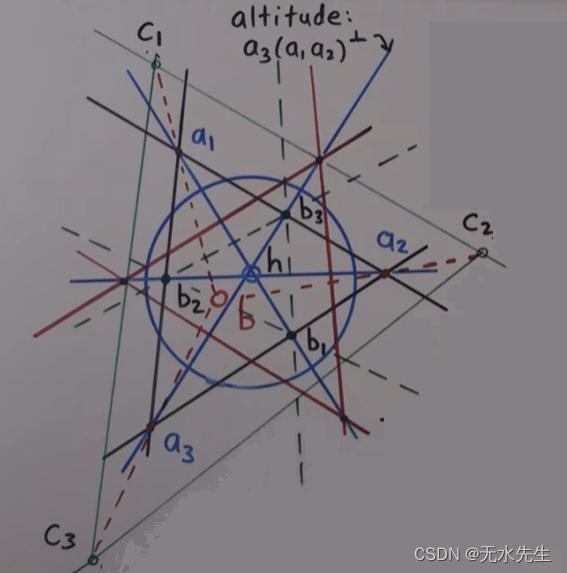
在这里插入图片描述
由于我们找到了正交三角形 $\overline{b_1b_2b_3}$ ，我们进一步，做出 $\overline{b_1b_2b_3}$ 的对偶三角形， $\overline{c_1c_2c_3}$ ，做法与上述相同，（做时要注意下标对应！）
连接 $\overline{a_1c_1}$ 、 $\overline{a_2c_2}$ 、 $\overline{a_3c_3}$ ，此三条线交于一点b，b就是三角形 $\overline{a_1a_2a_3}$ 的射影中心，从这一点发射的射线，将三角形 $\overline{a_1a_2a_3}$ 映射成三角形 $\overline{c_1c_2c_3}$ ，在空间中用锥体更加直观。