Leetcode:NO.84 柱状图中最大的矩形单调栈

本文主要是介绍Leetcode:NO.84 柱状图中最大的矩形单调栈，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

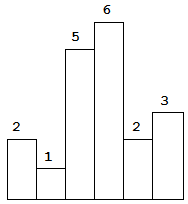
在这里插入图片描述
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

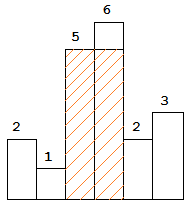
在这里插入图片描述
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:输入: [2,1,5,6,2,3]
输出: 10

链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram

解题记录

分析一下题目，其实可以转化为求子数组中最小值*数组长度的最大值的问题

1.暴力解法

直接通过两个循环遍历所有情况，然后获得最有解：

public class Solution {public static int largestRectangleArea(int[] heights) {int len = heights.length, maxArea = -1;for (int i = 0; i < len; i++) {int min = heights[i];for (int j = i; j < len; j++) {min = Math.min(min,heights[j]);maxArea = Math.max(maxArea, min*(j-i+1));}}return maxArea;}public static void main(String[] args) {int[] height = new int[]{2,1,5,6,2,3};System.out.println(largestRectangleArea(height));}
}

在这里插入图片描述

2. 中心扩散

由于子数组的面积跟最小值相关
这里转换一下思路我们遍历数组，把每个数值当成该最小值，找面积最大的子数组
以该数值两边如果比该数值大的话那么该值就是数组的最小值

class Solution {public static int largestRectangleArea(int[] heights) {int len = heights.length, maxArea = 0;for (int i = 0; i < len; i++) {int left = i, right = i;while (left>=0 && heights[left]>=heights[i]) left--;while (right<len && heights[right]>=heights[i]) right++;maxArea = Math.max(maxArea, (right-left-1)*heights[i]);}return maxArea;}
}

在这里插入图片描述

3.单调栈

中心扩展法就是求得该数左边和右边第一个比该数小的数的位置，通过位置计算宽度
可以通过单调栈，优先获取到每个数值对应的左边位置，和右边位置

class Solution {public static int largestRectangleArea(int[] heights) {int len = heights.length, res = 0;int[] left = new int[len], right = new int[len];Deque<Integer> stack = new ArrayDeque<>(len);for (int i = 0; i < len; ++i) {while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) stack.pop();left[i] = stack.isEmpty()? -1: stack.peek();stack.push(i);}stack.clear();for (int i = len-1; i >= 0; --i) {while (!stack.isEmpty() && heights[stack.peek()] >= heights[i]) stack.pop();right[i] = stack.isEmpty()? len: stack.peek();stack.push(i);}for (int i = 0; i < len ; i++) {res = Math.max(res, (right[i]-left[i]-1)*heights[i]);}return res;}
}

在这里插入图片描述

4.动态规划

使用动态规划的思想，如果前一个值比本值小的话，那么本值就是最小
如果前一个不比本值小的话，那么前一个值的临近小值一定大于等于本值的临近小值

class Solution {public static int largestRectangleArea(int[] heights) {int len = heights.length, res = 0;int[] left = new int[len], right = new int[len];for (int i = 0; i < len; ++i) {left[i] = i;int preIdx = i - 1;while (preIdx >= 0 && heights[preIdx] >= heights[i] ) {left[i] = left[preIdx];preIdx = left[i] - 1;}}for (int i = len - 1; i >= 0; --i) {right[i] = i;int preIdx = i + 1;while (preIdx < len && heights[preIdx] >= heights[i]) {right[i] = right[preIdx];preIdx = right[i] + 1;}}for (int i = 0; i < len; i++) {res = Math.max(res, (right[i]-left[i]+1)*heights[i]);}return res;}
}