【二分查找】Leetcode 74. 搜索二维矩阵【中等】

本文主要是介绍【二分查找】Leetcode 74. 搜索二维矩阵【中等】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

搜索二维矩阵

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

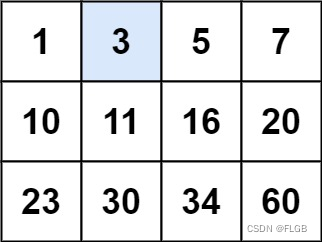
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

解题思路1

• 1、从矩阵的右上角开始查找。
• 2、如果当前元素等于目标值，则返回true。
• 3、如果当前元素大于目标值，则说明目标值在当前元素的左侧列，列索引减1。
• 4、如果当前元素小于目标值，则说明目标值在当前元素的下方行，行索引加1。
• 5、重复步骤2-4，直到找到目标值或者超出矩阵边界。

Java实现1

public class SearchMatrix {public boolean searchMatrix(int[][] matrix, int target) {if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {return false;}int rows = matrix.length;int cols = matrix[0].length;int row = 0;int col = cols - 1;while (row < rows && col >= 0) {if (matrix[row][col] == target) {return true;} else if (matrix[row][col] > target) {col--;} else {row++;}}return false;}public static void main(String[] args) {SearchMatrix solution = new SearchMatrix();int[][] matrix = {{1,3,5,7},{10,11,16,20},{23,30,34,60}};int target = 34;System.out.println("Target exists: " + solution.searchMatrix(matrix, target)); // Output: true}
}

时间空间复杂度1

• 时间复杂度：O(m + n)，其中m为矩阵的行数，n为矩阵的列数。因为每次迭代都会将行索引或列索引移动一次，最多移动m + n次。

• 空间复杂度：O(1)。

解题思路2

• 1、首先对第一列进行二分查找，找到最后一个小于等于 target 的元素所在的行。
• 2、在找到的行中进行二分查找，确定 target 是否在该行中。

Java实现2

public class SearchMatrix {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length;int n = matrix[0].length; 二分查找第一列，找到最后一个小于等于 target 的元素所在的行int left = 0;int right = m - 1;while (left <= right) {int mid =  (left + right ) / 2;if (matrix[mid][0] == target) {return true;} else if (matrix[mid][0] < target) {left = mid + 1;} else {right = mid - 1;}}// 如果目标值不在矩阵的第一列，则在确定的行中继续进行二分查找if (right >= 0) {//确定搜索行数int row = right;left = 0;right = n - 1;while (left <= right) {int mid =  (left + right ) / 2;if (matrix[row][mid] == target) {return true;} else if (matrix[row][mid] < target) {left = mid + 1;} else {right = mid - 1;}}}return false;}public static void main(String[] args) {SearchMatrix solution = new SearchMatrix();int[][] matrix = {{1,3,5,7},{10,11,16,20},{23,30,34,60}};int target = 34;System.out.println("Target exists: " + solution.searchMatrix(matrix, target)); // Output: true}
}

时间空间复杂度2

• 时间复杂度为 O(log m + log n)，其中 n 是矩阵的列数，m 是矩阵的行数。
• 空间复杂度：O(1)。

这篇关于【二分查找】Leetcode 74. 搜索二维矩阵【中等】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---