本文主要是介绍概率论 —— 相关分布以及期望方差的求法汇总,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
离散型
1. 两点分布(伯努利分布)
在一次试验中,事bai件A出现的概du率为P,事件A不出现的概率为q=l -p,若以X记一次试zhi验中A出现的次数,则X仅取0、I两个值。
两点分布是试验次数为1的伯努利试验。
2. 二项分布
是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变。
二项分布是试验次数为n次的伯努利试验。
EX=np,DX=np(1-p)
3. 超几何分布
 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品数
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品数
记作X-H(N.M.n),其E(X)=nM/N
DX=E(X-EX)²
=E(X²)-2E(X)E(X)+E²(X)
=E(X²)-E²(X)
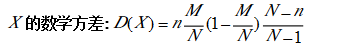
4. 泊松分布
 泊松过程是一个计数过程。
泊松过程是一个计数过程。
在0-t时与0-t+s时事件发生的次数独立且同服从参数为lamada的泊松分布。
这样按照时间走下来事件发生的次数就是一个泊松过程。
P(λ) E(X)=λ D(X)=λ
连续型
1. 均匀分布

在概率论和统计学中,均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为U(a,b)。
均匀分布的概率密度函数为:
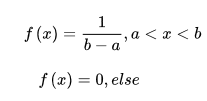

2. 指数分布

在概率理论和统计学中,指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。
(1)指数分布的概率密度函数
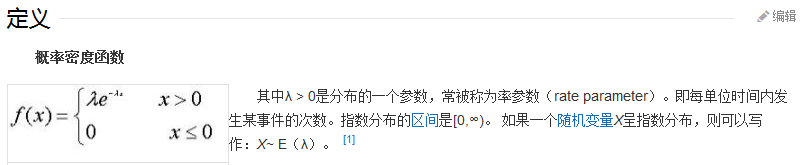
(2)指数分布的分布函数

E(X)=1/λ D(X)=1/λ²
3. 正态分布
若随机变量X服从一个数学期望为μ、方差为σ^2的
正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
正态分布具有两个参数μ和σ^2 的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ^2是此随机变量的方差,所以正态分布记作N(μ,σ2)。
μ是正态分布的位置参数,描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大,而取离μ越远的值的概率越小。正态分布以X=μ为对称轴,左右完全对称。正态分布的期望、均数、中位数、众数相同,均等于μ。
σ描述正态分布资料数据分布的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中。也称为是正态分布的形状参数,σ越大,曲线越扁平,反之,σ越小,曲线越瘦高。
正态曲线下,横轴区间(μ-σ,μ+σ)内的面积为68.268949%。
P{|X-μ|<σ}=2Φ(1)-1=0.6826
横轴区间(μ-2.58σ,μ+2.58σ)内的面积为95.449974%。
P{|X-μ|<2σ}=2Φ(2)-1=0.9544
横轴区间(μ-3σ,μ+3σ)内的面积为99.730020%。
P{|X-μ|<3σ}=2Φ(3)-1=0.9974
由于“小概率事件”和假设检验的基本思想 “小概率事件”通常指发生的概率小于5%的事件,认为在一次试验中该事件是几乎不可能发生的。由此可见X落在(μ-3σ,μ+3σ)以外的概率小于千分之三,在实际问题中常认为相应的事件是不会发生的,基本上可以把区间(μ-3σ,μ+3σ)看作是随机变量X实际可能的取值区间,这称之为正态分布的“3σ”原则。

4. 标准正态分布
当μ = 0,σ = 1时的正态分布是标准正态分布。
注意点:
1. 二项分布和超几何分布的区别与联系
超几何分布和二项分布的相同点为:随机变量均是取连续非负整数值的离散型分布列.
超几何分布和二项分布最明显的区别有两点:
①超几何分布是不放回抽取,二项分布是放回抽取,也就是说二项分布中每个事件之间是相互独立的,而超几何分布不是;
②超几何分布需要知道总体的容量,也就是总体个数有限;而二项分布不需要知道总体容量,但需要知道“成功率”.
超几何分布和二项分布二者之间也有联系:当总体很大时,超几何分布近似于二项分布,或者说超几何分布的极限就是二项分布。
2. 二项分布与泊松分布的区别与联系
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np。通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算。
3. 泊松分布与指数分布的关系
1、分布方面:
泊松分布参数bai是单位时间(或单位面du积)随机事件发生的zhi平均次数。泊松分dao布适用于描述单位时间内的随机事件数。指数分布可以用来表示独立随机事件的时间间隔,如旅客进入机场的时间间隔、中文维基百科新条目出现的时间间隔等。
2、应用方面:
指数分布被广泛使用。在日本工业标准和美国军用标准中,半导体器件的采样方案采用指数分布。此外,还用指数分布描述了大型复杂系统(如计算机)平均故障间隔时间的平均无故障时间分布。
泊松分布适用于描述每单位时间(或空间)的随机事件数。例如,某一时间到达服务设施的人数、电话交换所接到的呼叫数、公共汽车站等候的客人数、机器故障数、自然灾害数、产品缺陷数。在显微镜下分布在单位面积的细菌等。
3、然泊松分布和指数分布都有一个指数,兰姆达。但是这是两个概念。
泊松分布,期望值是朗姆达,意思就是强度。比如一段时间的人流量的强度。
指数分布,期望值的朗姆达的倒数。意思就是失效率。失效率是工作到某时刻尚未失效的产品。
这篇关于概率论 —— 相关分布以及期望方差的求法汇总的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






