本文主要是介绍G - Glyph Recognition Gym - 101623G(计算几何+二分),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题意:
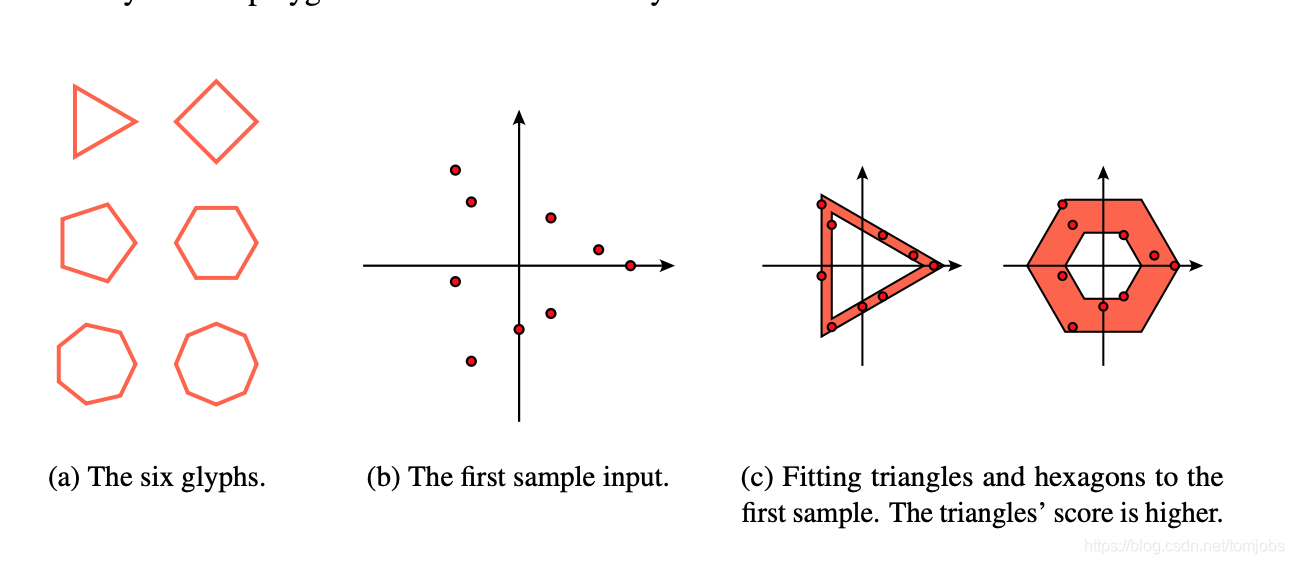
弄两个多边形覆盖图中所有点,要求里面多边形面积比上外面多边形面积值最大。
思路:
枚举用的是哪个多边形,则比值最大时,外面那个多边形覆盖所有点,里面那个多边形一个点都没有覆盖。二分就好了。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <iostream>using namespace std;const double eps = 1e-8;
const double pi = acos(-1);const int maxn = 1e3 + 7;
struct point
{double x,y;int id;point(){}point(double _x,double _y){x = _x;y = _y;}point operator+(point a){return point(x + a.x,y + a.y);}point operator-(point a){return point(x - a.x,y - a.y);}double operator*(point a){return x * a.y - y * a.x;}}a[maxn],p[10][15];
int n;
bool dcmp(double x,double y)
{if(x - y < eps && x - y > -eps)return 0;if(x - y > 0)return 1;return -1;
}double cal(point *p) { //算凸包面积double ans = 0;int cnt = p[0].id + 3;for(int i = 0;i < cnt - 1;i++){ans += (p[i] - p[0]) * (p[i + 1] - p[0]);}return fabs(ans) / 2;
}bool judge(point now,point *p,double mid) { //now是否在多边形内now.x /= mid;now.y /= mid;int cnt = p[0].id + 3;double ans = 0.0;for(int i = 0;i < cnt;i++) {point p1 = p[i % cnt],p2 = p[(i + 1) % cnt];ans += fabs((p1 - now) * (p2 - now));}ans = ans / 2;double area = cal(p);if(dcmp(area,ans) == 0) return true;return false;
}bool check1(double mid,point *p) { //覆盖所有点for(int i = 0;i < n;i++) {if(!judge(a[i],p,mid)) return false;}return true;
}bool check2(double mid,point *p) { //是否没有覆盖点for(int i = 0;i < n;i++) {if(judge(a[i],p,mid)) return false;}return true;
}void init() {for(int i = 0;i <= 5;i++) {for(int j = 0;j < i + 3;j++) {p[i][j].id = i;double rad = 2 * pi / (i + 3) * j;double x = cos(rad),y = sin(rad);p[i][j].x = x;p[i][j].y = y;} }
}int main() {#ifndef ONLINE_JUDGEfreopen("D:in.in", "r", stdin);freopen("D:out.out", "w", stdout);#endifinit();scanf("%d",&n);for(int i = 0;i < n;i++) {scanf("%lf%lf",&a[i].x,&a[i].y);}double ans = 0.0;int pos = 0;for(int i = 0;i <= 5;i++) {double l = 0,r = 5e7;double ans1 = 0.0;double ans2 = 0.0;while(r - l > eps) { //外层比例double mid = (l + r) / 2;if(check1(mid,p[i])) {r = mid;} else {l = mid;}}ans1 = l * l;l = 0,r = 5e7;while(r - l > eps) {double mid = (l + r) / 2;if(check2(mid,p[i])) {l = mid;} else {r = mid;}}ans2 = r * r;if(ans < ans2 / ans1) {ans = ans2 / ans1;pos = i;}}printf("%d %.8f\n",pos + 3,ans);return 0;
}
这篇关于G - Glyph Recognition Gym - 101623G(计算几何+二分)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






